Gehört zu: Astrofotografie
Siehe auch: Belichtungszeiten, ASI294MC Pro, Tracking
Benutzt: WordPress Latex-Plugin
Stand: 15.04.2023
Astrofotografie: Hintergrundlimitiert
Wieso “hintergrundlimitiert”?
Von “hintergrundlimitiert” spricht man, wenn der Bildhintergrund so hell ist, dass das Kamerarauschen (Ausleserauschen plus Dunkelstromrauschen; Read Noise + Dark Noise) im Vergleich zum Photonenrauschen (Sky Noise) des Himmelshintergrundes vernachlässigbar klein wird.
Wenn ich meine Einzelfotos in diesem Sinne schon hintergrundlimitiert habe, kann ich durch Verlängerung der Einzelbelichtungszeit keine Verbesserung des SNR im Summenbild mehr erreichen (bei gleicher Gesamtbelichtungszeit), da bei längerer Belichtung die Lichtverschmutzung dominieren würde.
Wie genau ist der Begriff “hintergrundlimitiert” definiert?
Es gibt keine verbindliche Definition dafür, ab welcher Zahl das Kamerarauschen gegenüber dem Photonenrauschen des Hintergrunds (Sky Noise) vernachlässigbar klein wird, aber Mischa Schirmer hat einmal in einem Forum als denkbare Definition genannt, dass das Photonenrauschen des Hintergrunds mindestens drei mal größer sein muss als das Kamerarauschen.
Quelle: https://www.astronomicum.de/forum/35/275
Youtube Video von Daniel Nimmervoll:
Wenn wir also Read Noise und Dark Noise vernachlässigen wird aus der generellen Gleichung
\( TotalNoise = \sqrt{TargetNoise^2 + ReadNoise^2 + DarkNoise^2 + SkyNoise^2} \)
die vereinfachte Gleichung:
\( TotalNoise = \sqrt{TargetNoise^2 + SkyNoise^2} \)
Wann ist mein Astrofoto hintergrundlimitiert?
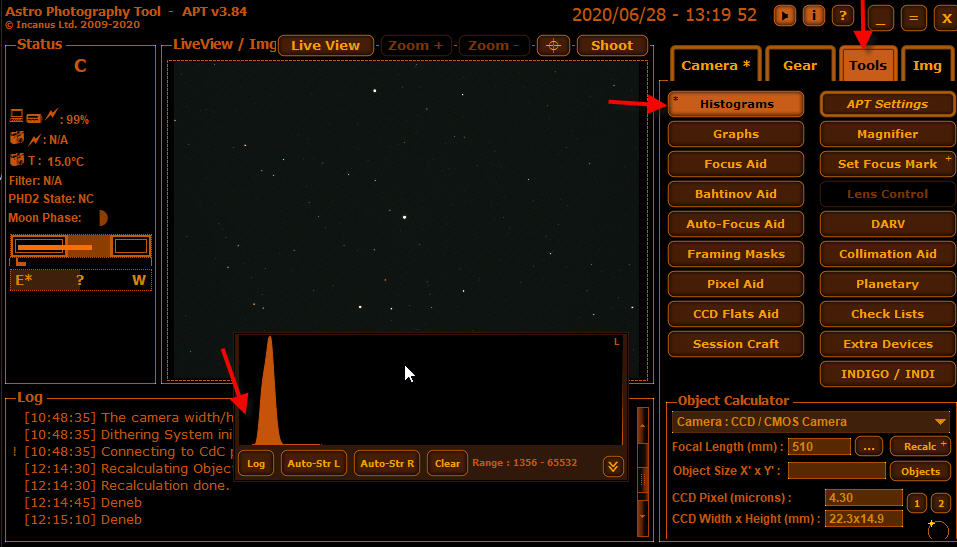
Ob ein Foto hintergrundlimitiert ist, kann man am Histogramm alleine nicht ablesen, weil man dem Histogramm nicht ansieht, wie hoch das Rauschen ist und schon gar nicht, wie hoch der Anteil des Kamerarauschens am Gesamtrauschen ist. Es ist aber sicher ein gutes Zeichen, wenn der Histogrammberg deutlich vom linken Bildrand losgelöst ist.
Messung des Kamerarauschens (Dunkelstromrauschen + Ausleserauschen)
Wir machen ca. 20 Dark-Frames und daraus ein Master-Dark. Im Master-Dark ist das Dark-Noise (quasi) verschwunden und nur noch das Dark-Signal vorhanden. Wir merken uns natürlich die Sensor-Temperatur, die Belichtungszeit und das Gain (ISO) dieser Darks.
- So ein Master-Dark können wir mit der Software Fitswork leicht erstellen: Fitswork-Menüleiste -> Datei -> Masterdark / -flat erstellen
Wir subtrahieren dann von jedem Einzel-Dark dieses Master-Dark. Das Ergebnis ist jeweils ein Dark in dem das Dark-Signal abgezogen ist und nur noch das DarkNoise übriggeblieben ist. Beispielsweise können wir das mit der Software Fitswork ganz einfach machen.
- So eine Subtraktion machen wir z.B. mit der Software Fitswork: Fitswork Bilder öffnen dann Menüleiste -> Bilder kombinieren -> Subtrahieren
- Das Einzel-Dark muss dabei das selektierte Foto sein, das Master-Dark muss im Hintergrund liegen.
- Als Ergebnis erhalten wir ein Bild, in dem nur noch das Kamerarauschen enthalten ist, weil wir das Dunkelstrom-Signal abgezogen haben
- Von so einem “nur Noise”-Bild bestimmen wir die Standardabweichung. Auch das können wir beispielsweise mit der Software Fitswork ganz einfach machen.
- Evtl. mitteln wir den Wert der Standardabweichung über mehrere dieser Einzel-Darks (Fitswork: Rechte Maustaste -> Bildstatistik zeigen).
- Dieser Wert der Standardabweichung ist ein Maßzahl für das Dunkestromrauschen (gemessen in ADU). Genaugenommen ist natürlich auch ein gewisser Teil Ausleserauschen darin, also sagen wir mal dieser Wert ist eine Maßzahl für das Kamerarauschen.
- In meinem Beispiel (240 s, Gain 121, 18° C) erhalte ich als Wert des Kamerarauschens 32 ADU
Mit meiner Astro-Kamera ASI294MC Pro habe ich folgendes mit Dark Frames gemessen:
| Temperatur | Belichtungszeit | Gain | Kamera-Rauschen |
| -10° C | 120 s | 300 | 75 ADU |
| -10° C | 120 s | 200 | 26 ADU |
| -10° C | 60 s | 200 | 21 ADU |
| -10° C | 30 s | 200 | 19 ADU |
| -10° C | 20 s | 300 | 51 ADU |
Messung des Himmelshintergrunds
Wir bezeichnen ein Foto als “hintergrundlimitiert”, wenn das Rauschen des Himmelshintergrunds mindestens dreimal so groß ist, wie das Kamerarauschen (Dunkelstromrauschen + Ausleserauschen).
Wir müssen also nun den Himmelshintergrund im zur Frage stehenden Einzelfoto (Light-Frame) messen. Wenn wir das einfach so im original Light-Frame machen würden, hätten wir zusätzlich zum Himmelshintergrund ja noch das Dunkelstrom-Signal und das Dunkelstrom-Rauschen darin. Das Dunkelstrom-Signal können wir abziehen, das Dunkelstrom-Rauschen nicht. Also subtrahieren wir von dem Light-Frame unser Masterdark.
Also in der Software Fitswork:
- Menüleiste Datei -> Open -> das Master-Dark
- Menüleiste Datei -> Open -> ein Light-Frame
- Menüleiste Bilder kombinieren -> subtrahieren
Wenn wir nun im so bereinigten Light-Frame einen kleinen Bereich, wo nur Hintergrund ist, messen (z.B. wieder mit Fitswork), so erhalten wir den Wert des Hintergrund-Signals als “Average” und den Wert von Hintergrund-Rauschen plus Dunkelstriom-Rauschen als “Standardabweichung” (gemessen jeweils in ADU). Wir haben also den korrekten Signal-Wert, aber (noch) nicht den korrekten Rausch-Wert. Um den “richtigen” Rauschwert des Hintergrunds zu bekommen, können wir die Tatsache benutzen, dass das Hintergrund-Signal einer Poisson-Verteilung genügt. Also:
\( Standardabweichung = \sqrt{Mittelwert} \)Deshalb können wir auch sagen, das die Wurzel aus dem Signal (Average) im Hintergrund des bereinigten Light-Frames muss mindesten 3 mal so hoch sein, wie das oben gemessene Kamerarauschen (Dunkelstromrauschen+…).
Bei meinem Beispiel (Light-Frame mit 60 s, Gain 121, 18 C) komme ich auf ein Hintergrund-Signal von 12000 ADU, was einem Hintergrund-Rauschen von 109,5 ADU entspricht (Wurzel aus 12000), was gerade etwas über unserer Grenze von dreimal Kamera-Rauschen (3 x 32 ADU = 96 ADU) liegt. Das 60s Foto ist also bei mir hintergrundlimitiert.
Mit meiner Astro-Kamera ASI294MC Pro habe ich folgendes mit Light Frames am Standort “Bundesstrasse” gemessen:
| Temperatur | Belichtungszeit | Gain | Ort | Hintergrund-Signal | Hintergrund-Rauschen | Kamera-Rauschen | Faktor |
| -10° C | 120 s | 300 | Bundesstrasse | 27700 ADU | 166 ADU | 75 ADU | 2,2 |
| -10° C | 120 s | 200 | Bundesstrasse | 15400 ADU | 124 ADU | 26 ADU | 4,8 |
| -10° C | 60 s | 200 | Bundesstrasse | 8300 ADU | 91 ADU | 21 ADU | 4,3 |
| -10° C | 30 s | 200 | Bundesstrasse | 4860 ADU | 70 ADU | 19 ADU | 3,7 |
| -10° C | 20 s | 300 | Kiripotib | 2600 ADU | 51 ADU | 51 ADU | 1,0 |
Ich hatte eine maximale Belichtungszeit von 120s wegen der Trackinggenauigkeit meiner Montierung AZ-GTi bei f=135mm schon gefunden.
Mit einem Gain von 200 bin ich dann deutlich Hintergrundlimitiert….
Maßeinheiten: ADU, Elektronen, Photonen
Mit Fitswork können wir unmittelbar in Einheiten von ADUs pro Pixel über die Belichtungszeit arbeiten. Wenn wir eine Elektronenrate haben wollen, müssen wir das Unity Gain der Kamera kennen. Bei Unity Gain wäre ein ADU gleich einem Elektron.
Wenn man von der Anzahl Elektronen zurück auf die Anzahl Photonen schließen will, benötigt man die sog. Quanteneffizienz “QE” des Sensors…
Wenn die Software die echten ADU-Werte (z.B. 14 Bit) hochgechnet auf z.B. 16 Bit, muß man dass ggf. auch noch korrigieren…
Lessons learned
Nachdem die Genauigkeit meines Trackings mit der HEQ5 Pro auch ohne Autoguiding ausreichend ist, wäre nur noch die minimale Belichtungszeit für meine Einzelfotos (bei der “Hintergrundlimitierung” eintritt) genauer zu bestimmen. In der nächsten sternklaren Nacht werde ich Aufnahmen probieren mit Belichtungszeiten: 10s, 20s, 30s, 60s bei Gain 121 und Kühlung auf -10 Grad und dazu passende Darks machen.