Gehört zu: Astronomie
Siehe auch: Sonnensystem, Kosmologie, Hertzsprung-Russel-Diagramm, Kopernikus, Kepler, Parallaxe, Hubble-Konstante, Delta Cepheiden
Benutzt: Fotos aus Wikipedia, Latex- Plugin für WordPress
Status: 08.09.2022
Astronomie: Entfernungsbestimmung
Links
https://libernaturaererum.files.wordpress.com/2012/10/vermessung.pdf
Überblick
- Längeneinheiten in der Astronomie
- Vom Erdumfang zum Urmeter
- Erathostenes Erdumfang
- Aristarch von Samos: Erde – Mond – Sonne
- Parallaxe des Mondes
- Parallaxe der Sonne
- Bessel: Parallaxe von Fixsternen
- Standardkerzen: Delta Cepheiden
- Standardkerzen: Supernovae vom Typ Ia
- Hubble: Rotverschiebung
Längeneinheiten in der Astronomie
Im heute geltenden SI-System ist die Einheit der Länge das Meter.
Vom Erdumfang zum Urmeter
1791 beschloss die verfassungsgebende Versammlung in Paris, die verschiedenen auf der Welt verwendeten Längenmaße zu vereinheitlichen. Das neue Längenmaß sollte später das “Meter” werden. Es wurde als zehn-millionster Teil des Viertels desjenigen Erdumfangs festgelegt, der Paris und den Nordpol berührt, definiert. 1793 wurde das Meter in Frankreich gesetzlich eingeführt.
Dazu musste man also die Länge des Erdumfangs bestimmen. Siehe dazu weiter unten und “Die Jagd nach dem Meter: Das Urmeter”. Nach heutigen Messungen beträgt der Umfang der Erde ca. 40000 km.
1960 wurde dieses “Urmeter” durch eine neue Definition im SI-System abgelöst.
Wegen der großen Entfernungen im Weltall benutzen die Astronomen gern andere Längeneinheiten.
Im Sonnensystem: Die Astronomische Einheit
Im Sonnensystem misst man die Entfernungen gerne in sog. Astronomischen Einheiten (A.E.). , was die mittlere Entfernung Erde-Sonne bedeuten soll.
Dazu muss man die Entfernung Erde-Sonne bestimmen. Weiter unten wird beschrieben, wie diese Entfernung durch Messung der Parallaxe bestimmt werden kann. Kennt man die Entfernung Erde-Sonne, kann man die Entfernung der anderen Planeten (Merkur, Venus, Mars, Juptier,…) mittels der Keplerschen Gesetze berechnen.
Die Astronomische Einheit wurde 2012 durch die IAU (Internationale Astronomische Union) als exakt 1 A.E. = 149 597 870 700 m festgelegt. Dadurch ist gleichzeitig auch das Parsec (s.u.) festgelegt.
In der Milchstraße: Lichtjahre
Ein Lichtjahr ist die Entfernung, die das Licht (im Vakuum) in einem Jahr zurücklegt.
Die Lichtgeschwindigkeit ist im SI-System festgelegt als: 299.792.458 m/s
Tabelle 1: Was ist ein Lichtjahr
| Größe | Wert | Einheit | Formel |
| Lichtgeschwindigkeit | 2,99792458 108 | m/s | |
| Julianisches Jahr | 365,25 | Tage | |
| Julianisches Jahr | 3,1558 107 | Sekunden | Tage*60*60*24 |
| Lichtjahr | 9,4607 1015 | m | Geschwindigkeit * Zeit |
| Lichtjahr | 1 | ly |
Damit ergibt sich:
\( 1 \space Lichtjahr = Lichtgeschwindigkeit \cdot Länge eines Jahres = 2,99792458 \cdot 10^8 \cdot 3,1558 \cdot 10^7 m = 9,46 \cdot 10^{15} \space m \)Das Lichtjahr wird gerne in populärwissenschaftlichem Zusammenhang benutzt.
Beispiel: Milchstraße
Der Durchmesser unserer Milchstrasse beträgt 100.000 Lichtjahre…
Beispiel: Proxima Centauri
Die Entfernung zu unserem nächstgelegenen Fixstern “Proxima Centauri” beträgt: 4,24 ly
Mit einem modernen Verkehrsflugzeug (1000 km/h) würde eine Reise dorthin 4,6 Mio Jahre dauern.
Längeneinheit: Angström
Bei ganz kleinen Längen (Mikroskop, Lichtwellenlängen etc.) verwendet 1 Angström = 0,1 Nano Meter (nm) = 10-10 m
Entfernungsbestimmung durch Messung der Parallaxe
Grundlage ist die Tatsache, dass alle Himmelskörper an die dahinter liegenden Hintergrundsterne (Himmelssphäre) projiziert erscheinen. Verändert der Beobachtungsort seine Lage, so verschiebt sich der projizierte Ort am Himmel. Diese parallaktische Verschiebung ist umso größer, je größer die Ortsveränderung des Beobachters und je näher das Gestirn ist. Eine Standortänderung eines Beobachters auf der Erde ergibt sich durch deren Rotation (tägliche Parallaxe), die Bewegung der Erde um die Sonne (jährliche Parallaxe) und die Bewegung der Sonne mitsamt den Planeten im Milchstraßensystem (säkulare Parallaxe).
Die Entfernung zu Fixsternen ausserhalb unseres Sonnensytems können wir durch Messung der “jährlichen Parallaxe”, also mit der Basis des Erdbahnradius von 150 Mio km bestimmen.
Entfernungseinheit: 1 Parsec (für Parallaxen Sekunde) – die Entfernung, in der die Parallaxe 1 Bogensekunde beträgt.
Bezeichnen wir die jährliche Parallaxe eines Sterns in Bogensekunden mit p und die Entfernung dieses Sterns in Parsec mit r, so gilt:
\( \Large r = \frac{1}{p} \\ \)Weil \( 1 \space Bogensekunde = \frac{2 \pi}{60*60*360} = 4,8481368 \cdot 10^{-6} \) im Bogenmass ist, ergibt sich das Parsec zu:
\( \frac{1 A.E.}{4,8481368 \cdot 10^{-6}} = \frac{149 597 870 700 \, m}{4,8481368 \cdot 10^{-6}} = 3,08567758 \cdot 10^{16} m \)Maßeinheiten der Länge im Vergleich
Tabelle 2: Maßeinheiten
| Größe | Wert | Einheit | Formel |
| Astronomische Einheit | 149,5978707 | Mio km | 1 Mio = 106 (festgelegt) |
| Astronomische Einheit | 1,495978707 1011 | m | 103 m = 1 km (festgelegt) |
| Astronomische Einheit | 1 | A.E. | |
| Winkel | 1 | Bogensekunde | |
| Winkel | 4,8481368 10-6 | Bogenmass | 2 pi / (60*60*360) |
| Parsec | 3,08567758 1013 | km | A.E. / Winkel |
| Parsec | 3,08567758 1016 | m | 103 m = 1 km |
| Parsec | 3,26 | ly | 10 * 3,08567758 / 9,46 |
| Parsec | 1 | pc | |
| Julianisches Jahr | 365,25 | Tage | festgelegt |
| Julianisches Jahr | 31 557 600 | s | 365,25*24*60*60 |
| Lichtjahr | 9,46 1015 | m | 299792458 m/s * 31557600 s |
| Lichtjahr | 1 | ly |
Zum Vergleich: 1 Parsec = 3,2 Lichtjahre.
Sehr gerne wird von Astronomen die daraus abgeleitete Entfernungseinheit “Mega Parsec” verwendet…
Erathostenes: Die Erdumfang
Erste bekannte Bestimmung des Erdumfangs stammt von Erathostenes (276 v.Chr – 194 v.Chr.), einem Freund des Archimedes.
Erathostenes beobachtete, das in Syene (heute Assuan) die Sonne bei ihrem Höchststand ganz senkrecht in einen tiefen Brunnen schien – Assuan liegt auf dem Wendekreis. In Alexandria dagegen erreichte die Sonne bei ihrem Höchststand nicht die genaue senkrechte, sondern warf einen kleinen Schatten. Diesen Einfallswinkel der Sonne bestimmte er zu 1/50 eines Kreises, also ca. 7,2 Grad.
Die Entfernung von Alexandria nach Syene war damas durch Landvermessung bekannt, nämlich 5000 Stadien. Also musste der Erdumfang 50 * 5000 Stadien = 250000 Stadien sein. Die Frage ist nur noch, welche Länge hatte damals ein Stadie…
Abbildung 1: https://www.planet-wissen.de/gesellschaft/ordnungssysteme/kartografie_das_gesicht_der_erde/eratosthenesberechntedenerdumfangsehrgenau100~_v-gseapremiumxl.jpg”
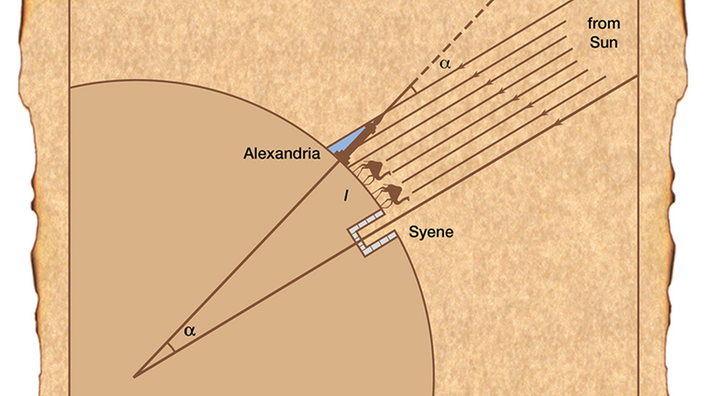
Abbildung 2: Encyplopaedia Britannica (Wikipedia: Eratosthenes_measure_of_Earth_circumference.svg)

Aristarch von Samos: Erde – Mond – Sonne
Aristarch von Samos (310-250 v.Chr.) hat versucht, die Entfernungen von Mond und Sonne in Relation zu setzen. Er nutzte dazu die Stellung dieser Gestirne bei Halbmond aus:
Abbildung 3: Aristarch von Samos
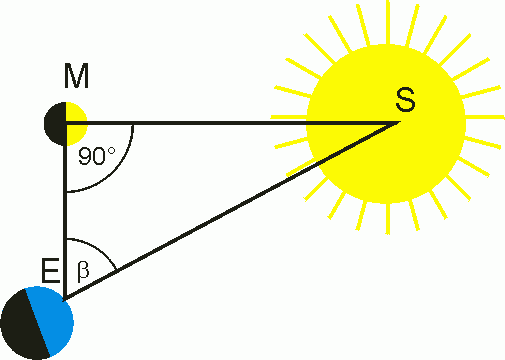
Quelle: https://www.leifiphysik.de/sites/default/files/images/5a15c1d5df48707705166eb72ed95511/505sonnenentfernung_nach_aristarch.gif
Aristarch hat den Winkel von Mitte Halbmond zu Mitte Sonne mit 87 “gemessen” (er sagte: “Ein Dreißigstel des Viertelkreises weniger als ein Viertelkreis”). Daraus ergibt sich das Verhältnis von Mondentfernung zu Sonnenentfernung wie 1 zu 19.
Die heutigen Zahlen sind:
- Entfernung Erde – Mond: 384400 km
- Entfernung Erde – Sonne: 150000 Mio km
Also ist das Verhältnis 1 zu 390.
Hier lag Aristarch also ziemlich weit daneben. Die Ungenauigkeit ist vielleicht verständlich, weil erstens der Halbmond nicht ganz so scharf zu bestimmen ist und zweitens so ein großer Winkel am Taghimmel auch nicht so einfach zu messen ist.
Trotz der – aus heutiger Sicht – großen Ungenauigkeit dieses ersten Versuchs von Aristarch, ist das Ergebnis für die damalige Zeit revolutiomär, denn bis dahin ging man davon aus, dass alle Gestirne am Himmel in etwa die gleiche Entfernung von der Erde haben – die sog. “Himmelskugel”.
Bestimmung der Entfernung Erde – Mond durch Parallaxe
Die Entfernung zum Mond kann durch Messung seiner täglichen Parallaxe bestimmt werden.
Dazu nimmt man zwei Beobachter auf möglichst unterschiedlichen geografischen Breiten und möglichst gleicher geografischer Länge…
Ptolemäus (160 – 125 v.Chr.) konnte die tägliche Parallaxe des Mondes anhand der Beobachtung von Mondfinsternissen zu 53,9′ bestimmen, was recht gut zu dem heutigen Wert von 57′ passt.
Mit einem Erdradius von R = 6371 km ergibt sich daraus eine Entfernung von D = R /Bogenmass(57′).
\( D = \Large \frac{6371 km}{57 \cdot \frac{2 \pi}{360 \cdot 60}} = \frac{6371 km}{0,0165806279}\)Daraus ergibt sich eine Entfernung Erde – Mond von D = 384244 km
Bestimmung der Entfernung Erde – Mars durch Parallaxe
Den ersten Erfolg mit einer Parallaxemessung hatte J. D. Cassini (1625-1712), der 1672 die Marsparallaxe bestimmte. Von England und von Frankreich aus wurde zu gleicher Zeit der Ort des Planeten Mars unter den Fixsternen gemessen und damit seine Entfernung von der Erde bestimmt. Mit Hilfe des dritten Keplerschen Gesetzes konnten damit auch die Entfernungen der Erde und der übrigen Planeten von der Sonne bestimmt werden. Als Abstand Erde – Sonne (die astronomische Einheit) erhielt man einen Wert von 134 bis 140 Millionen Kilometer. (Heute gültiger Wert: 149,6 Millionen km.)
Bestimmung der Entfernung Erde – Sonne durch Parallaxe
Die Entfernung zur Sonne kann durch Messung ihrer täglichen Parallaxe bestimmt werden.
Die täglichen Parallaxe der Sonne beträgt am Erdäquator 8,8” (z.B. Venusdurchgang).
Venusdurchgänge 1761 und 1769
Mit einem Erdradius von R = 6371 km ergibt sich daraus eine Entfernung von D = R /Bogenmass(8,8″).
\( D = \Large \frac{6371 km}{8,8 \cdot \frac{2 \pi}{360 \cdot 60 \cdot 60}} = \frac{6371 km}{0,0000426636}\)Daraus ergibt sich eine Entfernung Erde – Sonne von D = 149 331 032 km.
Die Entfernungseinheit: 1 Astronomische Einheit (A.E.) = 150 Mio km – wird benutzt, um Entfernungen innerhalb unseres Sonnensystems anzugeben.
Sterne in unserer Nähe: Parallaxe
Wilhelm Bessel (1784-1846) konnte als erster eine Fixstern-Parallaxe messen und zwar beim Stern 61 Cyg. Bessel hat in den Jahren 1837/38 die jährliche Parallaxe von 61 Cyg zu 0,31″ bestimmt, was eine Entfernung von \( \frac{1}{0,31} = 3,2258 \) Parsec also \( 3,2258 \cdot 3,259 = 10,5 \space Lichtjahre \) ergibt. Neuere Messungen der Parallaxe ergeben: 0,286″.
Damit war auch das Heliozentrische Weltbild endgültig bestätigt. Die Erde bewegt sich um die Sonne. Die Parallaxen sind ein Spiegelbild dieser Erdbewegung.
Durch genaue Messung der Parallaxe kann mann heute die Entfernungen im Sonnensystem und auch zu den Sternen in der näheren Umgebung bis ca. 300 Lichtjahre messen.
Standard-Kerzen: Delta Cepheiden
Henrietta Swan Leavitt (1868-1921) entdeckte 1912 die “Perioden-Leuchtkraft-Beziehung” anhand von Aufnahmen der Kleinen Magellanschen Wolke (SMC).
Cepheiden sind Pulsationsveränderliche – ihre Leuchtkraft bzw. Helligkeit verändert sich streng periodisch.
Die Helligkeit hängt bei Cephiden mit der Länge ihrer Periode zusammen (Perioden-Leuchtkraft-Beziehung)
Cepheiden dienen zur Entfernungsmessung im Kosmos: aus der Beobachtung der Periodendauer kann man direkt auf die absolute Helligkeit schließen. Durch die Messung der scheinbaren Helligkeit dann mit dem Entfernungsmodul die Entfernung berechnen werden.
Die Cepheiden in der SMC haben ja alle die gleiche Entfernung, deshalb gilt die Beziehung zwischen Periode und Helligkeit auch für die absolute Helligkeit, also die Leuchtkraft. Es ist ledigleich eine Kalibrierung erforderlich.
\(m – M = 5 \cdot (\lg{r} – 1) \)
1913 gelang Ejnar Hertzsprung (1873-1967) dann die Bestimmung der Entfernung einiger Cepheiden der Milchstraße, womit die Entfernung (und damit die absolute Helligkeit) zu allen Cepheiden kalibriert werden konnte.
Die Cepheiden-Methode reicht bis knapp zu den Galaxien des Virgo-Galaxienhaufes (Entfernung bis 23 Mpc) und dient so auch der Entfernungsbestimmung extragalaktischer Systeme.
Standard-Kerzen: Supernovae vom Typ Ia
Eine Supernova ist das kurzzeitige, helle Aufleuchten eines massereichen Sterns am Ende seiner Lebenszeit durch eine Explosion, bei der der ursprüngliche Stern selbst vernichtet wird. Die Leuchtkraft des Sterns nimmt dabei millionen- bis milliardenfach zu, er wird für kurze Zeit so hell wie eine ganze Galaxie.
Man kennt zwei grundsätzliche Mechanismen, nach denen Sterne zur Supernova werden können:
- Massereiche Sterne mit einer Anfangsmasse von mehr als etwa acht Sonnenmassen, deren Kern am Ende ihrer Entwicklung und nach Verbrauch ihres nuklearen Brennstoffs kollabiert. Hierbei kann ein kompaktes Objekt, etwa ein Neutronenstern (Pulsar) oder ein Schwarzes Loch, entstehen. Dieser Vorgang wird als Kollaps- bzw. hydrodynamische Supernova bezeichnet.
- Sterne mit geringerer Masse, die in ihrem vorläufigen Endstadium als Weißer Zwerg Material (z. B. von einem Begleiter in einem Doppelsternsystem) akkretieren, durch Eigengravitation kollabieren und dabei durch einsetzendes Kohlenstoffbrennen zerrissen werden. Dieses Phänomen wird als thermonukleare Supernova oder Supernova vom Typ Ia bezeichnet.
Supernovae vom Typ Ia sind eine gute Stardardkerze und können so zur Entfernungsbestimmung benutzt werden.
Die absolute Helligkeit (Helligkeit in einer Entfernung von 10 Parsec) einer Supernova vom Typ Ia lässt sich mit Hilfe der sog. “Phillips-Beziehung” rechnerisch ermitteln.
Wenn wir dann die scheinbare Helligkeit messen, ergibt sich daraus die Entfernung r (in Parsec), da ja die scheinbare Helligkeit mit dem Quadrat der Entfernung abnimmt.
\(r = 10^{1+\frac{m-M}{5}} \)Auf diese Weise konnte 1923 die Entfernung des Andromedanebels (M31) ermittelt werden.
Hubble-Konstante
Edwin Hubble (1889-1954) beobachtete in den Spektren von Galaxien eine Rotverschiebung.
Er interpretierte diese Rotverschiebung z als Dopplereffekt hervorgerufen durch eine Fluchtgeschwindigkeit v der Galaxien.
\(\displaystyle z = \frac{v}{c} \)Edwin Hubble konnte 1929 nachweisen, dass diese Rotverschiebung (interpretiert als Fluchtbewegung) mit der Entfernung D der Galaxien zunimmt. Es waren zwar nur 18 Galaxien, die Hubble untersuchte, doch mit wachsender Zahl hat sich dieses Ergebnis bestätigt. Dieser Zusammenhang ging als Hubble-Effekt in die Kosmologie ein.
\(\displaystyle v = H_0 D \)Das Hubble-Gesetz zeigt einen linearen Zusammenhang zwischen Fluchtgeschwindigkeit v und der Distanz D mit einer Proportionalitätskonstante, der Hubble-Konstanten H0. Die Linearität hat jedoch nur im nahen Universum ihre Gültigkeit, nämlich bis zu einem maximalen Abstand von gut 400 Mpc oder z kleiner als 0,1. Für weiter entfernte Objekte bricht die Linearität zusammen.
Bei größeren Geschwindigkeiten (d.h. groß relativ zur Lichtgeschwindigkeit) müssen zusätzlich die relativistischen Effekte berücksichtigt werden. Das erfolgt dann mit HIlfe der sog. “Robertson-Walker-Metrik” und die “Friedmann-Gleichung“.