Gehört zu: Kosmologie
Siehe auch: Expansion des Universums, Gravitation, Relativitätstheorie, Einsteinsche Feldgleichungen
Benutzt: Latex-Plugin für WordPress
Stand: 16.04.2025
Die Friedmann-Gleichung
In der Kosmologie wollen wir das Universum als Ganzes beschreiben; d.h. die zeitlichen Entwicklung vom Urknall bis heute und weiter…
Am Ende kommen wir zum vielgenannten “Standardmodell der Kosmologie“…
Alexander Friedmann (1888-1925) wollte die Einsteinschen Feldgleichungen der ART als Ausgangspunkt benutzen, musste für sein kosmologisches Modell dann noch zusätzliche Annahmen über die Verteilung von Materie, Energie, etc. im Universum machen.
Das sog. Kosmologische Prinzip stellt sich solche Verteilungen als isotrop (das Universum sieht in alle Richtungen gleich aus) und homogen (das Universum sieht an jedem Punkt gleich aus) vor. Wobei das alles nur bei der Betrachtung sehr großer Skalen der Fall ist (hunderte von Mega Parsec).
Unter diesen einfachen Annahmen (Homogenität und Isotropie) konnte Friedmann aus der Einsteinschen Formel der Allgemeinen Relativitätstheorie seine einfacheren sog. Friedman-Gleichungen ableiten (s. unten).
Die Expansion des Universums
Zur Expansion des Universums hatte ich einen eigenen Blog-Post geschrieben.
Unter der Grundannahme von Homogenität und Isotropie können wir die Expansion des Universums durch den sog. Skalenfaktor a(t) beschreiben.
Kosmologisches Modell
Unter einem Kosmologischen Modell versteht man Lösungen der Einsteinschen Feldgleichungen, bei denen einige wenige Parameter und Annahmen als Ausgangspunkt genommen werden und dann die Entwicklung des Kosmos im Laufe der Zeit (t) beschrieben werden kann.
Unter den von Friedmann gemachten Annahmen
- Robertson-Walker-Metrik (Kosmologisches Prinzip)
- Ideale Flüssigkeit (Perfect Fluid) (Massendichte und Druck)
- Einsteins Feldgleichungen (Gravitation)
erhalten wir als Lösungen die Friedmann-Gleichungen.
Wir kennen die Einstein’schen Feldgleichungen:
\( \Large R_{\mu \nu} – \frac{1}{2} R g_{\mu \nu} + \Lambda g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu} \\\)dort haben wir auf der rechten Seite den Energie-Impuls-Tensor. Dieser ist für ideale Flüssigkeiten bekannt
und auf der linken Seite haben wir den Metrik-Tensor, den wir aus der Robertson-Walker-Metrik kennen.
In diesen so bekannten Tensoren stecken einige Parameter, die wir für ein konkretes kosmologisches Modell setzen müssen.
Parameter in Kosmologischen Modellen:
- Strahlungsdichte: Ωrad
- Materiedichte: Ωm (barionische und dunkle Materie)
- Dichte der dunklen Energie: ΩΛ (auch Vakuum-Energie genannt)
- Krümmungsparameter: k
Kosmologische Modelle als Lösung der Gleichungen
Ein wichtiger Bestanteil eines Kosmologischen Modells ist die zeitliche Entwicklung des Skalenfators a(t).
Je nach den Grundannahmen gibt es verschieden benannte Kosmologische Modelle.
| Name | Annahmen | Ergebnis | Bedeutung |
| De Sitter | ΩΛ = 1 (also Ωm=0 und Ωrad =0) | Konstanter Hubble-Parameter a(t) = a0 e Ht |
theoretisches Modell |
| Einstein – de Sitter | Ωm= 1 (also ΩΛ=0 und Ωrad =0) | ||
| Lambda CDM | Ωm=0.3, ΩΛ=0.7 (also Ωrad =0) | zur Zeit favorisiert | |
Abbildung 1: Kosmologische Modelle

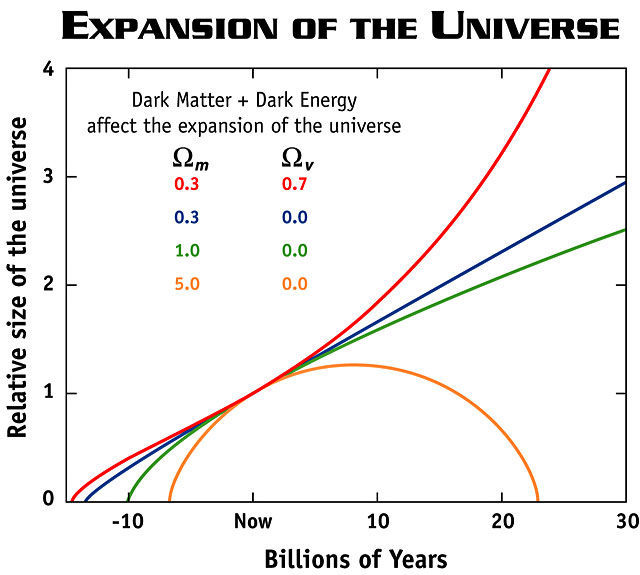
Copyright: NASA/WMAP Science Team
Das de-Sitter-Universum
Das einfachste kosmologische Modell ist das sog. “de Sitter”-Modell, das 1917 vom niederländischen Astronomen Willem de Sitter entwickelt wurde.
Beim de-Sitter-Universum bleibt der Hubble-Parameter als zeitlich konstant; also H(t) = H0 für alle t. Daraus würde sich der Skalenfaktor a(t) ergeben als:
\( \Large a(t) = a_0 \cdot e^{H_0 \cdot t}\\ \)Ein Universum mit diesem Kosmologischen Modell nennt man ein de Sitter Universum.
Dieses kosmologische Modell ist geht von folgenden Annahmen aus:
- Λ > 0
- ρ = 0 (und damit Ωm = 0)
Die Friedmann-Gleichung mit Newtonscher Mechanik
Youtube-Video: Josef Gassner: Von Aristoteles zur Stringtheorie
Wenn man zunächst ohne Relativitätstheorie (also nur mit der Klassischen Newtonschen Mechanik) rechnet, ergibt sich allein aus unseren Grundprämissen (Isotropie und Homogenität) und der Erhaltung der Energie (kinetische + potentielle) schon die klassische Friedmann-Gleichung. Später werden wir sehen, wie sich das relativistisch rechnet und dann für große Massen und große Abstände gilt…
Wegen der Homogenität können wir irgendeinen ganz beliebigen Punkt im Universum betrachten.
An jedem solchen Punkt im Universum haben wir eine gleiche Dichte ρ deren Wirkung ein Gravitationsfeld ist.
Im Newtonschen Ansatz ist diese Dichte allein die Massendichte, im relativistischen Fall käme noch die Energiedichte hinzu, die ebenfalls gravitativ wirken würde.
Wir betrachten dann einen Testkörper der Masse m im Abstand R von diesem Punkt.
Aufgrund der Expansion des Universums verändert sich dieser Abstand R mit der Zeit t gemäß dem Skalenfaktor:
\( R(t) = a(t) \cdot R_0 \) Wobei R0 der heutige Abstand sein soll
Dieser Testkörper hat nun eine Potentielle Energie (Epot) im Gravitationsfeld und eine Kinetische Energie (Ekin) aufgrund der Expansionsbewegung.
Als Kinetische Energie bekommen wir:
\( E_{kin} = \frac{m}{2} \dot{R}^2 \)Die Potentielle Energie bekommen wir, wenn wir die Gravitationskräfte betrachten, die auf den Probekörper wirken.
Als Gravitationswirkung haben wir die Masse der Kugel vom Radius R um den betrachteten Punkt. Da wir eine homogene Dichte ρ haben, ergibt sich diese Masse zu:
\( M = \frac{4}{3} \pi R^3 \rho \)Nach Newton können wir diesen Teil der Gravitation wie eine punktförmige Masse behandeln. Die Massen ausserhalb dieser Kugel heben sich nach dem Newtonschen Kugelschalen-Theorem gegenseitig zu Null auf.
Das Gravitationspotential der Kugel ist also:
\( \Phi(r) = – \frac{G \cdot M}{r}\)und als Potentielle Energie unserer Probemasse ergibt sich:
\( E_{pot} = \Phi(R) \cdot m = – \frac{G \cdot M \cdot m}{R}\)Wenn wir hier die Masse M, nach obiger Formel einsetzen, erhalten wir:
\( E_{pot} = – \frac{G \cdot m}{R} \cdot \frac{4}{3} \pi R^3 \rho \)und schließlich:
\( E_{pot} = – \frac{4}{3} \pi \cdot G \cdot m \cdot R^2 \cdot \rho \)Die Sume aus kinetischer und potentieller Energie soll gleich bleiben:
\( E_{kin} + E_{pot} = \frac{m}{2} \dot{R}^2 – \frac{4}{3} \pi \cdot G \cdot m \cdot R^2 \cdot \rho = E = const. \)Wenn wir dass mit 2 multiplizieren und die Masse m herauskürzen bekommen wir:
\( \dot{R}^2 – \frac{8}{3} \pi \cdot G \cdot R^2 \cdot \rho = 2 \frac{E}{m} = const. \)Wenn wir \( \dot{R}(t) \: und \: R(t) \) einsetzen bekommen wir::
\( (\dot{a} \cdot R_0)^2 – \frac{8}{3} \pi \cdot G \cdot (a \cdot R_0)^2 \cdot \rho = 2 \frac{E}{m} = const. \)Dies können wir noch durch R02 dividieren und bekommen:
\( (\dot{a} )^2 – \frac{8}{3} \pi \cdot G \cdot (a )^2 \cdot \rho = 2 \frac{E}{m \cdot {R_0}^2} = const. \)Nun dividieren wir noch durch a2 und bringen den Minus-Term nach rechts:
\(\Large \left(\frac{\dot{a}}{a}\right)^2 = \frac{8}{3} \pi \cdot G \cdot \rho \; – \: \frac{const}{a^2} \)Das ist schon die berühmte Friedman-Gleichung…
Damit die die Newtonsche Friedmann-Gleichung ganz analog der relativistischen aussieht, formen wir sie etwas um:
\(\Large \left(\frac{\dot{a}}{a}\right)^2 = \frac{8}{3} \pi \cdot G \cdot \rho \; – \: \frac{k \cdot c^2}{a^2} \)k nennen wir Krümmungsparameter; das wäre also:
\( \Large k = \frac{2 E}{m \cdot c^2 \cdot {R_0}^2} \)Dieser Krümmungsparameter wird uns später bei der Robertson-Walker-Metrik wieder begegnen.
Je nach dem wie der sog. Krümmungsparameter k ist sagt man:
- wenn k=0 ==> “flaches” Universum (Euklidische Metrik)
- wenn k>0 ==> “geschlossens” Universum (Zweidimensionale Metrik analog einer Kugeloberfläche)
- wenn k<0 ==> “offenes” Universum (Zweidimensionale Metrik analog einer Sattelfläche)
Im Falle k=0 würde sich für die Dichte ergeben:
\( \Large \rho_0 = \frac{3 \cdot \left(\frac{\dot{a}}{a}\right)^2}{8 \pi G} \)Oder, wenn wir für \(\frac{\dot{a}}{a} \) die Hubble-Konstate H einsetzen:
\( \Large \rho_0 = \frac{3 H^2}{8 \pi G} \)Diese Dichte nennen die Kosmologen gern die “kritische Dichte” und messen in ihren Modellen die Dichte dann gerne im Verhältnis zu dieser “kritischen Dichte”:
\( \Large \Omega = \frac{\rho}{\rho_0} = \frac{8 \pi G}{3 H^2} \rho \\ \)Aufgelöst nach ρ ergibt das:
\( \Large \rho = \frac{3 H^2}{8 \pi G} \cdot \Omega\\ \)Die Friedmann-Gleichung mit relativistischer Mechanik
Diesen Abschnitt muss ich noch überarbeiten…
Wir gehen aus von den Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie (ART)…
\( \Large R_{\mu \nu} – \frac{1}{2} R g_{\mu \nu} + \Lambda g_{\mu \nu} = \frac{8 \pi G}{c^4} T_{\mu \nu} \\\)Die Herleitung der Friedmann-Gleichung nimmt an, dass das Universum mit Materie, beschrieben als ideale Flüssigkeit (d.h. homogenen, isotrop und ohne Viskosität) angefüllt ist. Deshalb wurde auch der Energie-Impuls-Tensor einer idealen Flüssigkeit verwendet:
\(\Large T_{\mu \nu} = \left[ \begin{array}{rrrr} -\rho c^2 & 0 & 0 & 0\\ 0 & p & 0 & 0\\ 0 & 0 & p & 0\\ 0 & 0 & 0 & p\end{array} \right] \\ \)Wobei ρ(t) die Massendichte und p(t) der Druck ist.
Siehe auch: Viererimpuls
===================================================
Zur sog. Friedmann-Gleichung können wir der Wikipedia (https://de.wikipedia.org/wiki/Friedmann-Gleichung) folgendes entnehmen:
\( \displaystyle \frac{\dot a}{a}=H_{0}(\frac{\Omega_{m0}}{a^3}+(1-\Omega_{m0}))^{\frac{1}{2}} \)Wobei hier die sog. Hubble-Konstante H, die ja nicht wirklich konstant ist, vorkommt. In neuerer Zeit wird statt “Hubble-Konstante” auch der Begriff “Hubble-Parameter” verwendet.
Omega M = Anteil an Materie (barionisch und dunkle)
Omega groß Lambda = Anteil an dunkler Energie
Omega rad = Anteil Strahlungsenergie
k = Krümmung
Link: https://www.spektrum.de/lexikon/astronomie/friedmann-weltmodell/136