Gehört zu: Video
Siehe auch: WordPress, OBS Studio
Benutzt: Fotos aus Google Drive
Stand: 19.12.2022
Videos von Youtube
Ein Internet-Dienst, wo man nach Video-Clips suchen und diese sich dann anschauen kann. Man kann auch eigene Videos posten und auch Live-Videos hosten. Ein “Video-Portal” sagt man auch.
Die Firma Youtube wurde 2006 von Google aufgekauft.
Sehr häufig wird man bei Youtube Videos konsumieren, die andere gepostet haben. Es gibt dort Videos zu allen erdenklichen Themen, wie z.B. praktische Hilfen zum Do It Yourself, zur Astronomie, Vorlesungen zur Physik etc. etc. pp. und auch zu diversen Verschwörungstheorien.
Youtube Downloader
Man kann einzelne Videos auch herunterladen (downloaden). Das wird von Youtube selbst nicht unterstützt, aber es gibt es sog. Youtube-Downloader. Ich habe mehrere solche Downloader ausprobiert:
1. Freemake Video Downloder
Download von: https://www.freemake.com/de/free_video_downloader/
Der Download funktioniert.
Die Installation funktioniert (kostenlose Version): Version 4.1.13
Der Downloadeines Youtube-Videos (https://youtu.be/hrJViSH6Klo) geht erst schnell und wird dann nach etwa 52% sehr langsam…
In der kostenlosen Version wird ein Schriftzug über das ganze Video kopiert: “Freemake.com…”.
Ansonsten keine Bloatware und keine Download-Beschränkungen.
2. X2Download
ist ein Online-Service: https://x2download.com/de32
xyz
3. Free YouTube Download
In der neuesten Version unbrauchbar (viel Werbung und weitere Restriktionen)
4. 3 D Youtube Downloader
Wir von der Zeitschrift Chip empfohlen.
Download: https://www.chip.de/downloads/3D-Youtube-Downloader_145759161.html
Dieser Downloader funktioniert gut.
5. Firefox Add-on
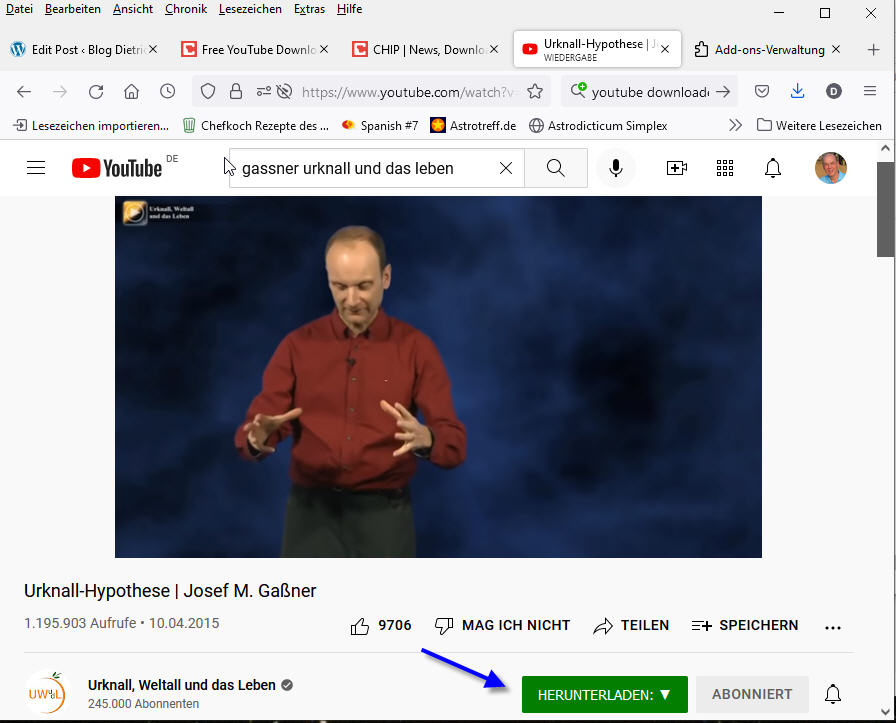
Im Firefox installiere ich das Add-on: “Easy Youtube Video Downloader Express”. Dann wird im Firefox, wenn ich ein Youtube-Video anschaue gleich darunter ein Schaltfläche “Download” eingebaut…
Abbildung 1: Youtube Downloader als Firefox Add-on (pCloud: YoutubeDownloader-01.jpg)
Youtube Videos in WordPress
Auch kann man einzelne Videos in seinen WordPress-Blog einbauen.
Beispiel 1: Youtube-Video zur Stromversorgung
Der einfachste Weg, ein Youtube-Video in ein WordPress Post aufzunehmen, ist es das Video in Youtube aufzurufen und dort die URL (oben in der Adresszeile) zu kopieren.
Diese URL kann ich nun in meinen WordPress-Post einfügen, wobei der Editor (bearbeiten) auf “visual” stehen muss und der Cursor dabei auf dem Anfang einer neuen Zeile stehen muss. Bei dieser Methode macht WordPress alles automatisch (mit der sog. “oEmbed Methode”) und ich kann die Art und Weise der Darstellung im WordPress-Post nicht weiter beeinflussen.
Eine alternative Möglichkeit ist es, beim auf Youtube sichtbaren Video unterhalb rechts auf “Share” (“Teilen”) zu klicken und dort die Option “embed” (“einbetten”) auszuwählen. Dann bekommt man ein HTML Snipplet mit iframe-Code, der kann kopiert werden und im WordPress-Post wieder eingefügt werden, allerdings im “Text” Mode des Editors. Wir haben dann alle Möglichkeiten des HTML-IFRAME-Konstrukts zur Verfügung.
Abbildung 2: Video von Youtube in WordPress-Post einbetten (embed)
Abbildung 3: TheNilsor Schrödinger-Gleichung (eingebettet)