Gehört zu: Astrofotografie, Stacking
Siehe auch: Deep Sky Stacker, PixInsight, Astro Pixel Processor, ComputerAcerBaer, Bildbearbeitung, StarNet, Plate Solving
Benutzt: Fotos aus Google Drive
Stand: 13.05.2025
Was ist neu in der Version 1.4.0-beta ?
Die Skriptsprache wurde auf Python umgestellt.
Der Siril-Befehl “preprocess” heisst jetzt “calibrate”. Ältere Skripts müssen entsprechend umgestellt werden.
Denoising und Sharpening durch die Seti Astro Cosmic Clarity Suite ist jetzt als Schnittstelle integriert in Siril und zwar mithilfe von Phyton-Skripts. Dabei werden Siril-Bilddateien hin in TIFF-Format konvertiert und nach dem Denoising bzw. Sharpening wieder zurück ins Siril-Format konvertiert.
Quellen
Ein Youtube-Video von Deep Space Astro: https://youtu.be/Y_fEO5slgX0?si=wVgw9IOTpKPKaYIG
Ein Youtube-Tutorial von Frank Sackenheim:
Das Youtube-Video von Cuiv “The Lazy Geek”: https://youtu.be/dEX9KbbzALc
Das YouTube-Video von “Deep Space Astro”: https://youtu.be/s3TJduagxrw
Astrofotografie mit der kostenlosen Software Siril
Siril ist eine kostenlose Software mit dem Schwerpunkt Stacking, kann aber noch einiges anderes mehr (Bildbearbeitung)…
Aufmerksam geworden bin ich auf Siril durch das unten angegebene YouTube-Video von Frank Sackenheim im März 2020. Dann hat Cuiv “The Lazy Geek” aus Tokio im August 2020 auch das Thema Siril aufgegriffen. Deswegen machte ich einen zweiten Versuch, Siril zu verstehen…
Dann bin ich bei der Beschäftigung mit Smart Telescopes im September 2023 erneut auf Siril gestossen, wobei mich die Möglichkeiten der Bildbearbeitung besonders beeindruckt haben, beispielsweise die Integration von StarNet.
Als Alternative zum traditionellen Deep Sky Stacker ist das modernere Siril vielleicht ganz interessant. Auch als kostenlose Alternative zu PixInsight kann Siril mit Background Extraction und fotometrischer Farbkalibrierung punkten.
Zusammenfassung Bildbearbeitung mit Siril (aus SuW 6/2024)
- Stacken
- Registrieren
- Kalibrieren
- Lineares Bild
- Hintergrund extrahieren
- Platesolving
- Farbkalibrierung
- Farbsättigung
- Stretching
- Asinh-Transformation (etwas)
- Histogramm-Stretching
Vorteile von Siril
- kostenlos
- Für Windows und Linux und MacOS
- Stacking mit vielen manuellen Einflussmöglichkeiten, aber auch “vollautomatisch” per Skript
- Nach dem Stacken: Bildnachbearbeitung:
- 1: Zuschneiden (Cropping)
- 2: Background Extraction
- 3. Platesolving
- 4: Color Calibration (auch photometrisch) <— Dazu Bild-Koordinaten erforderlich
- 5. Color Saturation
- 6. Sterne separieren (StarNet++)
- 7. Stretching the Histogram
- 8: Green Noise Reduction
- 9: Annotations
- 10: Deconvolution
- 11: Saving as TIFF, FITS, JPG oder PNG
- …
Besonderheiten von Siril
Im Gegensatz zu anderer Stacking-Software gibt es bei Siril zu beachten:
- Es sollte mit den Unterordnern: lights, darks, flats und biases gearbeitet werden (damit die Scripte zum Stacken funktionieren)
- Siril untersützt automatische Abläufe durch ausgeklügelte Scripts
- Siril kann sehr gut mit Narrowband-Filtern bei Farbkameras (OSC) umgehen
- Siril unterstützt photometrische Farbkalibrierung
- Siril hat starke Funktionen zur Nachbearbeitung von Astro-Fotos
- Siril hat eine integrierte StarNet-Funktion (erfordert eine Intel CPU mit AVX Advanced Vector Extensions)
Installation und Konfiguration
Software Download: https://www.siril.org/download/#Windows
Versionen:
- Version 1.4.0-beta2 (26. April 2025) (Änderung: Phython als Skript-Sprache)
- Version 1.2.6 (22. Jan 2025)
- Version 1.2.5 (22. Nov 2024)
- Version 1.2.4 (11. Sep 2024)
- Version 1.2.1 (Jan 26, 2024)
- Version 1.2.0 (Sep 15, 2023)
- Version 1.2.0-beta2 (March 12, 2023)
- Version 1.2.0-beta1 (Feb 24, 2023)
- Version 1.0.6 (18. Oct 2022)
- Version 1.0.3 (28. June 2022) (Änderung: Die Scrol-Balken sind verschwunden)
- Beta-Version: 0.99.8.1 (13. Februar 2021). Diese Beta-Version für die geplante Version 1.0 hat ein komplett verändertes GUI – deshalb helfen ältere Tutorials im Moment kaum noch.
Die Konfigurationsdatei ist: c:\users\<name>\AppData\Local\siril\config.ini
In dieser Config-Datei speichert Siril auch den Namen des letzten Working Directory, was man hier oder später auf der Siril-Komandozeile mit dem Befehl “cd” ändern kann (oder durch klicken auf das Symbol “Häuschen” – oben links).
Einstellen des “Themes“: Hamburger Menü -> Preferences -> User Interface -> Aussehen (Look and Feel): Dort können wir z.B. das “Dark Theme” auswählen.
Auch die Sprache können wir hier einstellen. Deutsch mögen viele da gern, aber dann muss man mit zum Teil komischen Übersetzungen leben und Tipps und Tricks aus der SiriL-Community sind mit “Englisch” meist besser zu verstehen…
Einstellen der “Language“: Hamburger Menü -> Preferences -> User Interface -> Language: Dort können wir z.B. “English [en]” auswählen.
Auch der Pfad zur Software StarNet muss hier eingebeben werden.
Siril Skripts
Skripts in SiriL sind einfach Dateien mit der Endung *.ssf
Die ersten Schritte mit Siril: Bildbearbeitung
Man kann Siril auch nur zur Bildbearbeitung (mit bereits gestackten Fotos) einsetzen. Dazu kann man so ein gestacktes Foto einfach in Siril laden (Links oben “OPEN”) und dann mit “Image Processing” bearbeiten.
Die Anzeige des Bildes kann man einstellen als “Linear”, “Autostretch” u.a. mit einem kleinen Drop-Down in der Mitte unteren Fensterleiste. Das wirkt nur auf die Anzeige, das Foto selbst bleibt unverändert.
Zum Speichern des Bildes als Bilddatei gibt oben rechts auf der Leiste zwei Symbole:
- Kleine Schaltfläche “Save”
- Rechts davon das Symbol “Pfeil nach unten”; das bedeutet: “Speichern unter” (quasi ein “Download”)
Bildnachbearbeitung: Zuschneiden
Durch das Stacken (speziell wenn man beim Fotografieren Dithering eingestellt hat) gibt es meist schmale dunkle Ränder, die wir jetzt abschneiden wollen.
- Input: Die aktive Bilddatei z.B. r_db_pp_Pacman_Lights_stacked.fit
- Mit der Maus auf einem Graubild (Red, Green, Blue) oder einem RGB-Bild ein Rechteck ziehen (wie Markieren),
- Klick mit der rechten Maustaste und auf “Zuschneiden” (“Crop”) klicken
- das zugeschnittene Bild wird von Siril automatisch gespeichert und im Fenster neu angezeigt
- Output: Dieselbe Bilddatei wie Input (Achtung: destruktiv!!!)
Bildnachbearbeitung: Hintergrund-Extraktion
Ähnlich wie in PixInsight kann auch SiriL den Bildhintergrund ermitteln und dann abziehen. Das macht man gerne um z.B. Gradienten zu entfernen.
- Input: Die aktive Bilddatei z.B. r_db_pp_Pacman_Lights_stacked.fit
- Menüleiste -> Bildbearbeitung (Image Processing) -> Hintergrund-Extraktion
- Samples für den Hintergrund manuell setzen (dahin wo kein Nutzsignal ist)
- Schaltfläche: “Compute Background”
- Korrektur: Drop-Down “Subtraktion” (oder, falls gewünscht: “Division”)
- Schaltfläche “Apply”
- Output: dieselbe Bilddatei wie Input (Achtung: destruktiv!!!)
- Schaltfläche: Schließen (Close)
Bildnachbearbeitung: Farb-Kalibrierung
Um schöne Sternfarben zu bekommen sollte man unbedingt eine Farb-Kalibrierung machen. Siril bietet dafür zwei Möglichkeiten an: “Farbkalibrierung” und “Photometrische Farbkalibrierung”.
Für die Photometrischen Farbkalibrierung muss Siril wissen, welche Sterne auf dem Bild zu sehen sind. Dazu versucht Siril im FITS-Header WCS-Koordinaten zu finden. Wenn die Kamera bereits Bilder im FITS-Format liefert (z.B. bei ASI-Kameras) muss nur noch die Bild-Aufnahme-Software (z.B. APT, N.I.N.A.) die Aufnahme-Koordinaten in den FITS-Header schreiben.
Wenn wir im FITS-Header (noch) keine Bild-Koordinaten haben, hat Siril zwei Wege diese nachträglich zu ermitteln:
- SIMBAD
- Platesolving: Dazu wird das Bild von Siril “ge-platesolved” (astrometrische Lösung)
Das Ganze läuft so:
- Input: Die aktive Bilddatei
- Menüleiste -> Bildbearbeitung (Image Processing) -> Farb-Kalibrierung -(Color Calibration) > Photometrische Farb-Kalibrierung (Photometric Color Calibration)
- Wenn noch keine Bild-Koordinaten (aus dem FITS-Header) gefunden wurden
- SIMBAD: Image Parameters: Eingabe Objektname (z.B. NGC281) gefundene Koordinaten aus einem Katalog übernehmen
- Wenn das Objekt nicht in SIMBAD-Katalog gefunden wurde: Plate Solving
- Brennweite (Focal distance): 510 mm
- Pixel Größe (Pixel Size): 4,6 µ
- Photometrischer Sternkatalog: NOMAD oder APASS anhand eines Sternkatalogs werden die sog. B-V-Indices der Sterne benutzt.
- Sternerkennung: Automatisch
- Hintergrund-Referenz: automatic detection (besser: selbst angeben)
- Normalisierung ja Kanal: On Lowest
- Schaltfläche: OK
- Output: Dieselbe Bilddatei wie Input (Achtung: destruktiv!!!)
- Schaltfläche: Close
Bildnachbearbeitung: Grünrauschen entfernen
Bei DSLRs und auch bei Astrokameras mit Farb-Sensor (“OSC”) haben wir oft eine Überbetonung der grünen Farbe.
- Input: Die aktive Bilddatei
- Menüleiste -> Bildbearbeitung (Image Processing) -> Grün-Rauschen entfernen (Remove Green Noise)
- Protection Method: Average Neutral
- Amount: 1.00
- Output: Schaltfläche “Apply” also dieselbe Bilddatei (Achtung: destruktiv!!!)
- Schaltfläche: Close
Bildnachbearbeitung: Farbsättigung anheben
Vor dem “Stretchen” soll man die Farbsättigung anheben.
- Input: Die aktive Bilddatei
- Menüleiste -> Bildbearbeitung (Image Processing) -> Farbsättigung (Color Saturation)…
- Hue: Global
- Amount: + 0.66
- Output: Schaltfläche “Apply” also dieselbe Bilddatei (Achtung: destruktiv!!!)
Bildnachbearbeitung: Histogramm-Transformation (Stretchen)
Menüleiste -> Bildbearbeitung
Hierzu hat SiriL mehrere Methoden:
- Arcsinh Transformation
- Generalized Hyperbolic Stretch Tranformation (“GHS”)
- Histogramm Transformation
Allgemein wird GHS empfohlen, wobei man sich da ersteinmal richtig einarbeiten muss (z.B. Tutorial https://siril.org/tutorials/ghs/).
Der Schwarzwert wird in einem separaten Vorgang verstellt…
Bildnachbearbeitung: Annotationen
Voraussetzung ist, dass das Bild vom Platesolving her WCS-Metadaten enthält.
In Siril sieht man in der Leiste unten rechts mehrere Symbole. Nach einem erfolgreichen Platesolving ist dort das Symbol “Kugel mit Koordinaten” aktiv (nicht mehr ausgegraut). Da kann man ja mal ausprobieren wie ein Koordinatennetz auf dem Bild dann aussieht. Das brauchen wir aber jetzt eigentlich noch nicht.
Rechte von diesem Symbol “Kugel mit Koordinaten” steht auf der Leiste ein Symbol “Konzentrische Kreise” damit schalten wir den Photometrie-Modus von Siril an. Wenn wir dann auf einen Stern im Bild klicken erscheint ein Fenster “PSF and quick photometry results” dort klicken wir unten auf “More Details…”. Dadurch werden wir auf eine externe Web-Seite geführt, wo wir den offiziellen Namen unseres Stern sehen und ins Clippboad kopieren. Mehr wollten wir hier nicht, nur den Namen.
Im nächsten Schritt gehen wir zurück zu unserem Bild in Siril und schalten photometrischen Modus aus. Dann können wir mit der rechten Maustaste in das Bild klicken und erhalten so ein Kontextmenü. Dort wählen wir aus “Search Object…” wo wir dann den oben gefundenen offiziellen Namen unseres Objekt eingeben….
Dies wir von Siril gespeichet in einem “User-DSO catalog”…
Bildnachbearbeitung: Speichern
Beim Speichern des bearbeiteten Bilden muss man aufpassen.
Obere Leiste -> Speichern als… (Symbol: “Pfeil nach unten”)
Erste Schritte mit Siril: Stacken (Kalibrieren, Registrieren,…)
Einstellen des Arbeits-Ordners (Arbeitsverzeichnis, Working Directory).
Wenn man später mit Scripts arbeiten will (was sehr empfehlenswert ist), müssen im Arbeits-Ordner die Unter-Ordner: biases, lights, darks, flats angelegt sein.
Dazu ordnet man seine Fotos eben in Ordner mit diesen Namen ein und gibt den übergeordneten Ordner als Arbeitsordner bei Siril an (Symbol “Häuschen” links oben).
Als erstes müssen in Siril unsere Bild-Dateien in das FITS-Format umgewandelt werden und in die genannten Unter-Ordner (denn wir wollen mit Scripts arbeiten) gelegt werden. Wenn die Bilder bereits im FITS-Format sind, versucht Siril mit SymLinks zu arbeiten.
Generell geschieht das Bearbeiten unserer Bilder päckchenweise. Diese “Päckchen” heißen bei Siril “Sequences” und müssen einen Sequence-Namen bekommen.
Beispiel Nummer 1: Farb-Kamera (OSC) mit Lights und Darks – ohne Flats und ohne Biases
Damit ich selber mal lerne, wie das mit dieser für mich neuen Software funktioniert, versuche ich es mit einem eigenen Fall. Ich habe gerade kürzlich (am 20.9.2020) eine Aufnahme vom Pacman-Nebel mit 60 Lights á 120 sec und 30 Darks (keine Flats und keine Biases) gemacht.
Wie man unten sieht, ist der ganze manuelle Ablauf sehr langwierig und fehleranfällig; deshalb sollte man für so einen immer wiederkehrenden Ablauf ein Siril-Script benutzen. Leider setzen die mitgelieferten Scripts immer voraus, dass man sowohl, Darks, als auch Light, Flats und Bias-Frames gemacht hat, was nicht immer der Fall ist. Das Zusatz-Programm “SiriL IC” sollte dabei helfen... Andererseits ist die Siril-Skriptspache auch recht einfach und man könnte da schnell etwas modifizieren…
Meine Pacman-Dateien befinden sich im Ordner: P:\Alben\Album_Astronomie\20200920_Bundesstrasse_Pacman, dieser wird also als erster Schritt als “Home” eingestellt.
Dark-Frames in eine Sequenz umwandeln
Zuerst müssen die Dark-Frames geladen und umgewandelt werden und einen Sequenz-Namen bekommen. Als Sequenz-Namen nehmen wir “Pacman_Darks”.
Auch wenn die Dateien schon im richtigen Format (FITS) vorhanden sind (weil meine ASI294MC Pro sie als FITs erstellt hat), muss diese “Umwandlung” in SiriL erfolgen, weil SiriL dann eine SEQ-Datei benötigt. Da die Dateien schon im (für SiriL) richtigen Format sind, werden sie lediglich kopiert.
Man kann beim “Umwandeln” auch “Symbolic Link” anhaken, dann werden die Dateien nicht echt kopiert, sondern es werden SymLinks erstellt. SymLinks funktionieren aber nur, wenn in Windows der “Developer Mode” eingestellt ist…
- Reiter: “Conversion”
- Input: Meine original Dark Frames
- Auf das Symbol “+” klicken und dann die gewünschten Dateien an ihrem Platz aussuchen (bei mir: P:\Alben\Album_Astronomie\20200920_Bundesstrasse_Pacman\Darks)
- Schaltfläche “Add” (unten rechts)
- Namen für die Sequenz angeben: “Pacman_Darks”
- Kästchen Symbolischer Link: anhaken
- Kästchen Debayern: nicht anhaken
- Schaltfläche “Umwandeln” klicken (Kästchen Symbolischer Link, Debayern nicht anhaken)
- Output: Sequence Pacman_Darks.seq
Die Ergebnisse einer solchen “Umwandlung” (auch “Konvertieren” genannt) werden oben im Arbeitsordner abgelegt. Zum Beispiel werden meine Darks im Arbeitsordner unter den Dateinamen Pacman_Darks_00001.fit, Pacman_Darks_00002.fit etc. kopiert (wobei “Pacman_Darks” der Sequenzname war) und es wird eine SEQ-Datei namens “Pacman_Darks.seq” im Arbeitsordner angelegt.
Die neu erstellte Sequenz wird von SiriL automatisch als “aktuelle Arbeits-Sequenz” geladen.
Master Dark erstellen
Ich mache dann aus diesen Darks ein sog. Master-Dark.
Das geht über den Reiter “Stacking” – wobei ein vorheriges Registrieren nicht erforderlich ist, da auf den Darks keine Sterne sind.
Für das Stacking machen wir folgende Einstellungen (wobei vom vorigen Schritt schon die richtige Sequenz ausgewählt bleibt):
- Input: Sequence Pacman_Darks.seq (sollte schon die aktuelle Arbeits-Sequenz sein)
- Reiter “Stacking”
- Stacking-Methode: Median-Stacking
- Normalisierung: Keine Normalisierung
- Schaltfläche: “Starte Stacking”
- Output: Das Ergebnis ist die Datei Pacman_Darks_stacked.fit im Arbeitsordner
Light Frames in eine Sequenz umwandeln
Dann müssen die Light-Frames geladen und umgewandelt werden und einen Sequenz-Namen bekommen. Als Sequenz-Namen nehmen wir “Pacman_Lights”
- Reiter: Conversion
- Input: Meine original Light Frames
- Auf das Symbol “+” klicken und dann die gewünschten Dateien an ihrem Platz aussuchen (bei mir: P:\Alben\Album_Astronomie\20200920_Bundesstrasse_Pacman\lights)
- Schaltfläche “Add” (unten rechts)
- Namen für die Sequenz angeben: “Pacman_Lights”
- Kästchen Symbolischer Link: anhaken
- Kästchen Debayern: nicht anhaken
- Schaltfläche “Umwandeln” klicken (Kästchen Symbolischer Link, Debayern nicht anhaken)
- Output: Sequence Pacman_Lights.seq
Die “umgewandeten” Lights stehen nun im Arbeitsordner unter den Dateinamen Pacman_Lights_00001.fit, Pacman_Lights_00002.fit,…
Die Ergebnisse einer solchen “Umwandlung” (auch “Konvertieren” genannt) werden oben im Arbeitsordner abgelegt. Zum Beispiel werden meine Lights in Arbeitsordner unter den Dateinamen Pacman_Lights_00001.fit, Pacman_Lights_00002.fit etc. kopiert (wobei “Pacman_Lights” der Sequenzname war) und es wird eine SEQ-Datei namens “Pacman_Lights.seq” im Arbeitsordner angelegt.
Die neu erstellte Sequenz wird von SiriL automatisch als “aktuelle Arbeits-Sequenz” geladen.
Master Dark von den Light Frames abziehen
Nun folgt das “Pre Processing” der Lights: Es wird das Master Dark abgezogen, wir haben keine Flats und auch keine Offsets/Biases…
- Input: Sequence Pacman_Lights.seq
- Reiter “Pre Processing”:
- Use Offset: Nein
- Use Dark: Ja und den Namen eintippen: Pacman_Darks_stacked.fit (sonst erscheint eine Meldung: “master.dark.fit.[Datei-Erweiterung]” nicht gefunden. / KEINE Dark-Frame-Benutzung: kann Datei nicht öffnen)
- Use Flat: Nein
- Ausgabe-Präfix: pp_
- Schaltfläche: “Starte Pre-Processing”
- Output: Sequence pp_Pacman_Lights.seq
Die pre-prozessierten Lights stehen nun im Arbeitsordner unter den Dateinamen: pp_Pacman_Lights_00001.fit, pp_Pacman_Lights_00002.fit,… (wobei pp_ ja der Präfix der Ausgabe-Sequenz ist).
Es wird eine SEQ-Datei namens “pp_Pacman_Lights.seq” im Arbeitsordner angelegt. Die neue Sequenz pp_Pacman_Lights.seq wird geladen.
De-Bayering der Light Frames
Das Debayering darf nicht zu früh im Workflow erfolgen. Unmittelbar vor dem Registrieren ist gut.
Vorher sollten wir noch einen Blick auf die Einstellungen für das De-Bayering werfen, welche man unter dem “Hamburger Menü” bei “Einstellungen” (Preferences) findet. Dort klicke ich “FITS/SER Debayer” an…
Das De-Bayering wird manchmal auch “De-Mosacing” genannt, weil das Bayer-Pattern z.B. RGGB auch gerne Mosaik genannt wird.
Also erfolgt das “Debayering” der Lights jetzt. In Siril steht die Funktion “Debayering” leider nur beim Reiter “Umwandeln (Convert)” zur Verfügung. Deshalb geht das so:
- Input: Die Light-Frames von denen das Master-Dark bereits abgezogen wurde
- Reiter: Umwandeln (Convert)
- Laden der Dateien: pp_Pacman_Lights_00001.fit, pp_Pacman_Lights_00002.fit,…,
- Schaltfläche “ADD” (Hinzufügen) (unten links)
- Sequenz-Namen vergeben: “db_pp_Pacman_Lights”
- Häckchen bei Debayering setzen
- Destination – Sequence Name – eintippen: db_pp_Pacman_Light
- Schaltfläche “Umwandeln” klicken
- Output: Sequence db_pp_Pacman_Light
Die “be-bayerten” Lights stehen nun als RGB-Dateien im Arbeitsordner unter den Dateinamen db_pp_Pacman_Lights_00001.fit, db_pp_Pacman_Lights_00002.fit,…
Es wird eine SEQ-Datei namens “db_pp_Pacman_Lights.seq” im Arbeitsordner angelegt. Die neue Sequenz db_pp_Pacman_Lights.seq wird geladen.
Registrieren der Light Frames
Das Registrieren legt alle Einzelbilder passgenau übereinander. Das ist als Vorbereitung für das Stacking erforderlich.
Dazu wird eines der Bilder als “Referenzbild” genommen und aus allen Bildern die Sterne identifiziert, welche dann mit denen im Referenzbild verglichen werden.
Als Referenzbild wird standardmäßig das erste Bild der Sequenz genommen, es sei denn, man bestimmt in der “Frame List” der Sequenz ein anderes als Referenzbild.
Das Registriren erfolgt im Einzelnen so:
- Input: Sequence db_pp_Pacman_Lights.seq
- Reiter “Registrieren”
- Registrieren alle Bilder der Sequenz
- Registrierungsmethode: “Allgemeine Sternausrichtung (Global Star Alignment) Deep Sky”
- Registrierungs-Layer: Grün
- Praefix: r_
- Algorithmus: bikubisch
- Schaltfläche: “Führe Registrierung aus”
- Output: Sequence r_db_pp_Pacman_Lights.seq
Die registrierten Bilder stehen nun im Arbeitsordner unter den Dateinamen: r_db_pp_Pacman_Lights_00001.fit, r_db_pp_Pacman_Lights_00002.fit,…
Es wird eine SEQ-Datei namens “r_db_pp_Pacman_Lights.seq” im Arbeitsordner angelegt. Die neue Sequenz r_db_pp_Pacman_Lights.seq wird geladen.
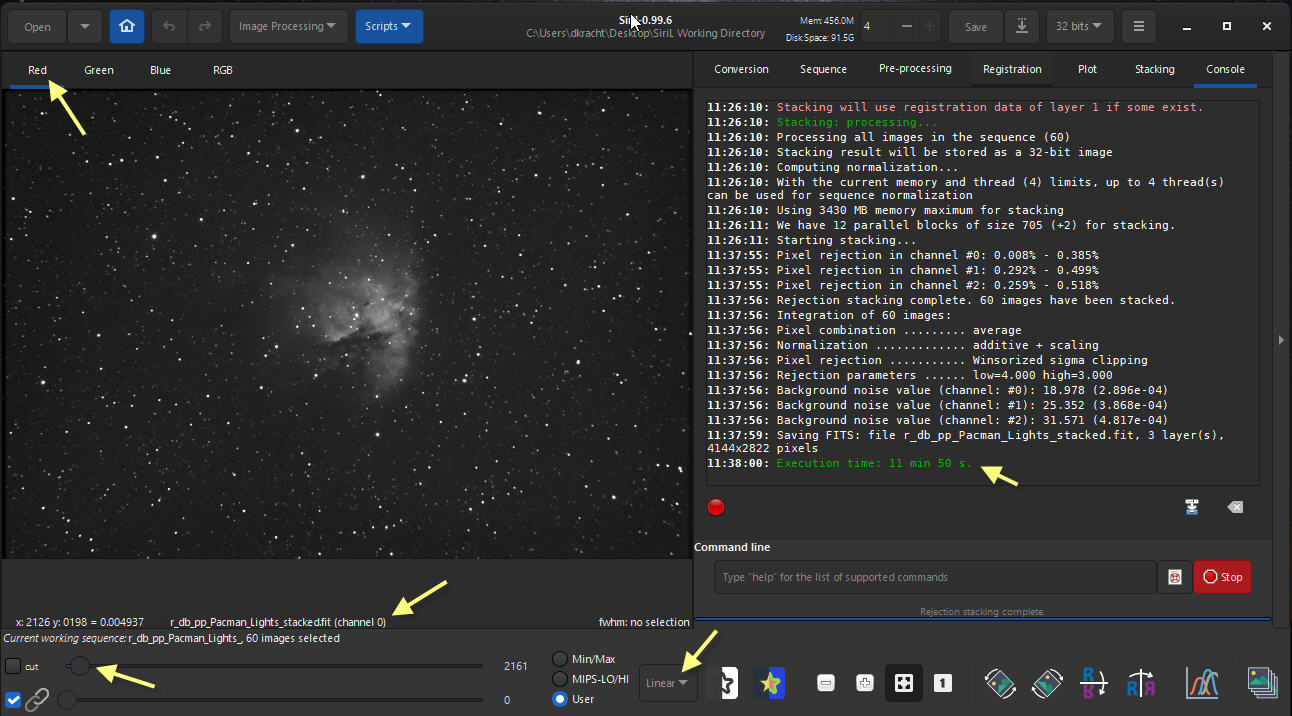
Stacken der Light Frames
Die registrierten Light Frames werden nun “gestapelt” englisch: stacked mit folgenden Einstellungen:
- Input: Sequence r_db_pp_Pacman_Lights.seq
- Reiter: Stacking
- Stacking-Methode: Durchschnittswert-Stacking mit Ausschleusung
- Normalisierung: Additiv mit Skalierung
- Ausschleusung: Wisorized Sigma Clipping
- Save in: r_db_pp_Pacman_Lights_stacked.fit
- Schaltfläche: “Starte Stacking”
- Output: Ergebnisdatei r_db_pp_Pacman_Lights_stacked.fit im Arbeitsordner (diese wird im SiriL-Fenster gleich angezeigt)
Abbildung 1: So sieht das in Siril dann aus (pCloud: Siril-Stacking-Ergebnis.jpg)