Physik

Physik: Wellengleichung

dkracht

Gehört zu: Physik
Siehe auch: Von Phythagoras bis Einstein, Schroedinger

Stand: 19.5.2022

Die Wellengleichung von D’Alembert

Die Wellengleichung, auch D’Alembert-Gleichung nach Jean-Baptiste le Rond d’Alembert (1717-1783), bestimmt die Ausbreitung von Wellen wie etwa Schall oder Licht.

Wenn das Medium oder Vakuum die Welle nur durchleitet und nicht selbst Wellen erzeugt, handelt es sich genauer um die homogene Wellengleichung, die lineare partielle Differentialgleichung zweiter Ordnung

\(\Large  \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} – \sum \limits_{i=1}^{n} \frac{\partial^2 u}{\partial x^2_i} = 0 \)

für eine reelle Funktion u (t, x1, x2,…,xn) der Raumzeit.

Hierbei bedeutet u die Auslenkung der Welle zur Zeit t am Ort x=(x1, x2,…,xn) und  n die Dimension des Raumes.
Der Parameter c ist die Ausbreitungsgeschwindigkeit der Welle, also bei Schall (im homogenen und isotropen Medium) die Schallgeschwindigkeit und bei Licht die Lichtgeschwindigkeit.

Eine einfache Lösung der Wellengleichung im eindimensionalen Raum (also n=1) ist beispielsweise die Wellenfunktion:

\( u(t,x) = \sin(x + ct) \)

Transversal – Longitudonal – Polarisierung

Eine Transversalwelle (Quer-, Schub- oder Scherwelle) ist eine Welle, bei der die Schwingung senkrecht zu ihrer Ausbreitungsrichtung erfolgt. Das Gegenteil ist eine Longitudinalwelle (Längswelle), bei der die Schwingung in Richtung der Ausbreitungsrichtung stattfindet.

Transversalwellen sind polarisierbar, da die Schwingung in der gesamten Ebene möglich ist, die senkrecht auf ihrer Ausbreitungsrichtung steht.

Stehende Wellen

Ein wichtiger Spezialfall sind sog. “Stehende Wellen”. Sie haben Knoten und Bäuche.

An einem festen Ende ist immer ein Knoten (Auslenkung Null) und an einem offenen Ende ist immer das Maximum eines Bauches.

Betrachten wir zwei feste Enden, so ist für die Gundschwingung: \( \frac{\lambda}{2} = L  \) und die Oberschwingungen ungerade Vielfache von lambda/2.

Weiterführendes

Stehende Wellen spielen eine Rolle

Physik: Thermodynamik – Wärmelehre

dkracht

Gehört zu: Physik
Siehe auch: Quantenmechanik, Physikalische Größen, Ideale Gase
Benutzt: WordPress-Plugin Latex

Stand: 29.06.2023   (neu: Zustandsgrößen)

Die Thermodynamik

Die Thermodynamik oder Wärmelehre ist eine natur- und ingenieurwissenschaftliche Disziplin. Das hauptsächliche Thema ist das Studium der Dampfmaschinen und die Frage, wie man Wärme in mechanische Arbeit umwandeln kann.

In der Thermodynamik (=Wärmelehre) werden wir erstmals irreversible Prozesse sehen. So etwas gab es in der klassischen Mechanik nicht.

Es gibt zwei Ansätze in der Thermodynamik: die statistische Sicht und die phänomenologische Sicht.  Statistisch werden ganz viele “Mikrozustände” betrachtet – Phänomenologisch geht es um die nach außen sichtbaren “Makrozustände”. Generell geht man davon aus, das sich die Mikrozustände in gewisser Weise vollkommen ungeordnet, eben stochastisch, verhalten.

Die physikalische Größe “Temperatur” wird in der Thermodynamik neu in die Physik eingeführt und ist eben eine “makroskopische” Größe.
Ausserdem wird eine weitere physikalische Größe, die “Entropie” eingeführt, die sehr schwer zu verstehen ist (dazu weiter unter: Zweiter Hauptsatz der Thermodynamik).

Phänomenologisch beschreiben wir den Zustand eines Systems oft durch die physikalischen Größen  Volumen, Druck und Temperatur (sog. Zustandsgrößen). Ein und der gleiche so beschriebene phänomenologischer Zustand kann dann aber durch viele unterschiedliche “mikroskopische” Zustände zustande kommen – eben statistisch.

Zustandsgrößen

Eine Zustandsgröße ist eine physikalische Größe, die – ggf. zusammen mit anderen – den Zustand eines physikalischen Systems zu einem gegebenen Zeitpunkt beschreibt und zwar unabhängig davon, auf welchem Wege er zustande gekommen ist; also unabhängig von der “Vorgeschichte” des Systems.

So sind beispielsweise Druck und Temperatur klassische Zustandsgrößen, aber die physikalische Größe “Arbeit” nicht. Letztere bezeichnet man dann als  sog. “Prozessgröße”.

Links:

Stichworte:

  • Wärme, Temperatur, Entropie
  • Ideales Gas
  • Irreversible Prozesse
  • Perpetuum mobile
  • Dampfmaschine
  • Thermodynamisches Gleichgewicht
  • Freiheitsgrade
  • Phasenraum

Temperatur – Thermodynamisches Gleichgewicht

Bringt man zwei Körper unterschiedlicher Temperatur zueinander in Kontakt, so stellt sich nach einer gewissen Zeit ein sog. “thermodynamisches Gleichgewicht” ein. Dann sind die Temperaturen beider Körper gleich.

So können wir schon einmal sagen, wann zwei Temperaturen gleich sind, aber haben noch keine Messskalen.

Temperatur – Messung der Temperatur

Die Temperatur ist eine Basis-Einheit des SI-Systems. Historisch wurde die Temperaturskala durch bestimme Fixpunkte festgelegt zwischen denen man dann interpolieren musste.

Als solche Fixpunkte hatte man benutzt Schmelzpunkte bzw. Gefrierpunkte von Wasser, Wasserstoff, Gold etc. Später ging man auch dazu über sog. Trippelpunkte als Fixpunkte zu benutzen.

Zur Interpolation zwischen solchen Fixpunkten nutzt man temperaturabhängege Eigenschaften von Körpern; wie z.B. die Längenausdehnung eines Metallstabes oder die Volumenausdehnung von Flüssigkeiten.

1948 wurde durch die 9. Generalkonferenz für Maß und Gewicht (CGPM) festgelegt, dass eine absolute thermodynamische Skala den Tripelpunkt des Wassers als einzigen fundamentalen Fixpunkt haben sollte. Vor allem die starke Abhängigkeit des Siedepunkts vom Luftdruck hatte die Temperatureichung über die bisherigen Fixpunkte schwierig gemacht. Der Tripelpunkt hingegen war leicht und eindeutig reproduzierbar.

1954 wurde das Kelvin von der CGPM in der bis zum 19. Mai 2019 gültigen Form definiert und zur Basiseinheit erklärt. Dadurch bekam zugleich das Grad Celsius eine neue Definition. Die Bezeichnung war zunächst „Grad Kelvin (°K)“ und wurde 1967 auf „Kelvin (K)“ geändert. Die Definition lautete seitdem: „Das Kelvin, die Einheit der thermodynamischen Temperatur, ist der 273,16-te Teil der thermodynamischen Temperatur des Tripelpunktes des Wassers.“.

2019: Anbindung an die thermische Energie: Die thermodynamische Temperatur ist direkt proportional zur thermischen Energie, mit der Boltzmann-Konstanten als Proportionalitätsfaktor  (1.380649 * 10–23 Joule/Kelvin). Solange die Einheiten von Energie (Joule) und Temperatur (Kelvin) unabhängig voneinander definiert waren, musste die Boltzmann-Konstante experimentell bestimmt werden. Diese Messungen wurden im Laufe der Zeit immer präziser und erreichten schließlich die Genauigkeit der Realisierung des Kelvin über den Tripelpunkt des Wassers. Damit war die Existenz zweier konkurrierender Definitionen nicht mehr zu rechtfertigen. Der Boltzmann-Konstanten wurde ein fester Wert in der Einheit J/K zugewiesen und das Kelvin dadurch direkt an das Joule gekoppelt. Der Wert der Boltzmann-Konstanten, die seitdem ein nur durch Konvention festgelegter Skalierungsfaktor ist, wurde so gewählt, dass das neue Kelvin möglichst genau mit dem alten übereinstimmte. Diese Änderung trat mit der Revision des Internationalen Einheitensystems am 20. Mai 2019 in Kraft.

Erster Hauptsatz der Thermodynamik

Der 1. Hauptsatz der Thermodynamik ist eine besondere Form des Energieerhaltungssatzes aus der Mechanik. In Worten bedeutet dies: Die Änderung der inneren Energie eines geschlossenen Systems ist gleich der Summe der Änderung der Wärmemenge und der Änderung der Arbeit.

In Formeln kann man das so ausdrücken:

\( \Delta U = \Delta Q + \Delta W \)

wobei:

  • U innere Energie des Systems
  • Q der Wärmeinhalt (Wärmemenge) des Systems – positiv, wenn dem System zugeführt – negativ, wenn aus dem System abgeführt
  • W die vom System geleistete mechanische Arbeit – positiv, wenn dem System zugeführt – negativ, wenn nach außen geleistet

Zweiter Haupsatz der Thermodynamik

Vorzugsrichtung von Prozessen. Der zweite Hauptsatz der Thermodynamik in der Formulierung von Rudolph Clausius (1822-1888) lautet: „Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von einem Körper niederer auf einen Körper höherer Temperatur ist.

Zustandsveränderungen können reversibel (wie in der klassischen Mechanik) oder irreversibel sein. Irreversible Prozesse laufen nur in einer Richtung ab und nicht umgekehrt. Bei reversiblen Prozessen bleibt die Entropie gleich, bei irreversiblen Prozessen nimmt die Entropie zu.

Der Zweite Hauptsatz der Thermodynamik kann mit Hilfe des Begriffs der Entropie auch so formuliert werden, dass die Entropie (eines geschlossenen Systems) niemals abnehmen kann.

Damit bekommt die Zeit eine Richtung.

Ideale Gase

Das Einfachste, mit dem sich die Thermodynamik gern befasst, sind die sog. Idealen Gase.

Boltzmann

Der österreichische Physiker Ludwig Boltzmann (1844-1906) beschreibt mit seiner “Boltzmann-Gleichung” die Dynamik eines idealen Gases und definiert die physikalische Größe Entropie über Mikro- und Makro-Zustände…

Thermodynamische Zustandsänderungen

Ein thermodynamischer Prozess kann zu einer thermodynamischen Zustandsänderung führen. Solche Zustandsänderungen (Prozesse) können reversibel oder irreversibel sein.

Zustandsgrößen beschreiben den Zustand eines thermodynamischen Systems; wobei es egal ist, auf welchem Wege man den betreffenden Zustand erreicht.

Typische Zustandsgrößen sind:

  • Volumen: V
  • Druck: p
  • Innere Energie: U
  • Entropie: S

Zustandsänderungen eines thermodynamischen Systems werden durch die Veränderung von Zustandsgrößen beschrieben.

  • Isotherme Zustandsänderung: Keine Temperaturänderung, also T=const. bzw. Δ U = 0
  • Adiabatische Zustandsänderung: Kein Wärmeaustausch, also Δ Q = 0

Veranschaulichen kann man sich solche Zustandsänderungen gut an einem p-V-Diagramm.

Klassische Definition der Entropie

Schon früher haben wir physikalische Größen kennengelernt, die “unabhängig vom Weg”  waren: In einem konservativen Kraftfeld war die Arbeit, die nötig ist, um von A nach B zu kommen weg-unabhängig. Deshalb konnen wir da die potentielle Energie und das Potential einführen.

Analoges macht in der Thermodynamik Rudolf Clausius (1822-1888) mit seiner klassischen Definition der Entropie (Formelzeichen: S). Die Entropie stellt so etwas wie ein Maß für die “Irreversibilität” dar. Die SI-Maßeinheit der Entropie ist Joule/Kelvin.

Zunächst betrachten wir nur Zustandsveränderungen – also Deltas. Damit definieren wir Entropieveränderungen als:

\( \Large \Delta S = \frac{\Delta Q}{T} \)

Der bekannte Carnot’schen Kreisprozess beschreibt im p-V-Diagramm ja eine geschlossene Kurve und ist insgesamt auch reversibel, da er ja aus vier Prozessschritten besteht, wovon jeder einzelne reversibel ist. Unsere Berechnungen des Carnot’schen Kreisprozesses hatten ja für die zwei isothermen Prozessschritte (w=warm, k=kalt) ergeben:

\( \Large\frac{\Delta Q_w}{T_w} + \frac{\Delta Q_k}{T_k} = 0  \)

Was uns zu einer generellen Formel (ohne Beweis) führt:

\( \Large \oint_\alpha \frac{d Q}{T} = 0 \)

für reversible Prozesse, die im p-V-Diagramm eine geschlossene Kurve “α” bilden.

In Analogie zum Potentialbegriff in einem Kraftfeld können wir auch hier ein “Potential” definieren, das wir “Entropie S(A)” am Aufsetzpunkt “A” nennen:

\( \Large S(A) = \int_O^A \frac{d Q}{T} \)

Mit einem festzusetzenden Referenzpunkt “O” .
Die physikalische Größe Entropie kann man in diesem Sinne sehr abstrakt definieren. Der Vorteil ist, dass die Entropie nun tatsächlich eine Zustandsgröße ist.

Statistische Definition der Entropie

Ludwig Boltzmann wird 50 Jahre nach Clausius eine schöne statistische Definition der physikalischen Größe Entropie geben.

Ein thermodynamischer Makrozustand (z.B. Druck eines Gases) kann durch sehr viele Mikrozustände der Gas-Moleküle (also Orte und Impulse) realisiert werden. Da wir es mit gigantisch großen Anzahlen von Molekülen zu tun haben setzen wir die Statistik ein und kommen zu Aussagen über Wahrscheinlichkeiten von Anordnungen (oder Unordnungen).

Die klassische Definition der Größe Entropie ist:

\( \Large S = k_B \log{P} \)

Wobei kB die Boltzmann-Konstante ist und P die Wahrscheinlichkeit mit der ein Makrozustand durch Mikrozustände eigenommen wird.

Durch die Benutzung des Logarithmus’ wird die Entropie zu einer richtigen extensiven (d.h. mengenartigen) physikalischen Größe. Wir können Entropie-Mengen sinnvoll addieren.

Die Frage ist dann noch, wo wir den Nullpunkt der Entropie setzen. Dazu hat Max Planck vorgeschlagen dass der Nullpunkt da liegen soll, wo es nur noch einen einzigen Mikrozustand gibt, durch den der Makrozustand realisiert werden kann. Das wäre ein ideales Kristallgitter in absoluter Ruhe. Also bei T=0 soll auch S=0 sein. Statt der Wahscheinlichkeit P benutzen wir dann also die Anzahl Mikrozustände Ω, die den Makrozustand realisieren. Max Planck war es auch, der vorgeschlagen hatte, die in der Formel vorkommende Konstante “Boltzmann-Konstante” zu nennen.

Damit kommen wir zu der berühmten Folmel, die auch auf Boltzmanns Grabstein auf dem Wiener Zentralfriehof steht:

\(\Large S = k_B \ln{\Omega} \)

 

 

 

Physik: Gravitation

dkracht

Gehört zu: Himmelsmechanik
Siehe auch: Die Keplerschen Gesetze, Schwarzes Loch, Newton, Langrange-Punkte, Ebbe und Flut, Kraftfeld und Potential
Benutzt: WordPress-Plugin MathJax-Latex

Stand: 25.2.2022

Die Grundkräfte

Die Gravitation ist eine der vier Gundkräfte (Wechselwirkungen) im Standardmodell der Teilchenphysik.

Kraftfelder, wie das der Gravitation, können wir durch das zugehörige Potential-Feld beschreiben.

Das Gravitationsgesetz

Im Jahre 1668, formulierte Isaac Newton (1642-1727) das berühmte Gravitationsgesetz:

\( \Large F = G \frac{m \cdot M}{r^2}  \)

aus dem sich die Keplerschen Gesetze herleiten lassen…

Das Besondere der Erkenntnis von Newton ist nicht nur die Formulierung als eine einzige Formel, sondern auch, dass die Gravitationskraft zwischen allen Körpern im Universum wirkt. Beispielsweise kreisen die Jupitermonde gemäß diesem Gesetz um den Jupiter und ebenfalls kreisen Doppelsterne etc. aufgrund der Gravitation umeinander…

Zu den Zeiten Newtons beschäftigte sich die Physik in der Hauptsache und fast ausschließlich mit Mechanik. Newton (und Leibnitz) entwickelten die Infenitesimalrechung (engl. Calculus) mit der die Bewegung mechanischer Systeme durch die Wirkung von Kräften berechenbar gemacht werden konnte. Siehe dazu mein separater Artikel Newtonsche Mechanik.

Isaac Newton hat auch sehr viel über das Licht geforscht. Stichworte dazu wären: Teilreflektion, Newtonsche Ringe,…

Die Größe der Gravitationskonstante G wurde erst viel später durch das berühmte Experiment “Gravitationswaage” von Henry Cavendish (1731-1810) bestimmt.

In der Wikipedia finden wir:

\( \Large G = (6{,}674\,30\pm 0{,}000\,15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} \)

Eine ähnliche Formel wie hier für die Gravitationskraft zwischen zwei Massen haben wir in der Elektrostatik für die Elektrische Kraft zwischen zwei elektrischen Ladungen: Das Coulomb-Gesetz.

Die Gezeitenkraft

Ein ausgedehner Körper wird in einem Gravitationsfeld auseinander gezogen, weil die Gravitationskraft ja mit der Entfernung abnimmt. Die “Vorderseite” eines Körpers wird stärker angezogen als die “Hinterseite”. Je größer die Abmessung des Körpers in Richtung Vorderseite/Hinterseite ist, desto größer die auseinanderziehende “Gezeitenkraft” als Differenz der Kräfte vorne/hinten..

Die Erdanziehung

Wie wir alle aus der Schule wissen, haben wir auf der Erdoberfläche eine Gravitationsbeschleunigung von ca. 9,81 m/s2

Das Gravitationsgesetz (s.o.) können wir auch schreiben als:

\( \Large a = G \frac{M}{r^2}  \)

Wenn wir Kraft = Masse mal Beschleuigung, also F = m * a, benutzen.

Wenn wir den mittleren Erdradius als 6371 km annehmen, sind wir auf der Erdoberfläche also im Mittel 6371 km vom Erdmittelpunkt entfernt.
Die Erdmasse beträgt laut Wikipedia ca. 5,9772 * 1024 kg

Bei bekanntem Erdradius, bekannter Erdmasse und bekannter Gravitationskonstante kann man sich die mittlere Gravitationsbeschleunigung an der Erdoberfläche also ausrechnen:

\( \Large a = G \frac{5,9772 \cdot 10^{24}}{6371000^2} = 9,82  \)

Oder andersherum: Wenn man die Gravitationsbeschleunigung gemessen hat, den Erdradius kennt und die Gravitationskonstante misst (wie Henry Cavendish s.o.), kann man die Erdmasse bestimmen…

Die Kreisbahn (Kreisbewegung)

Für eine Kreisbahn mit dem Radius R wäre eine Zentripedalkraft erforderlich von:

\( F_Z = m \cdot \frac{v^2}{R}\)

So eine Zentripedalkraft soll durch die Gravitation des Zentralkörpers der Masse M bewirkt werden. Diese Gravitationskraft ist:

\( F_G = G \cdot \frac{m \cdot M}{R^2}\)

Rechnerisch ergibt sich daraus als Kreisbahngeschwindigkeit (sog. Erste kosmische Geschwindigkeit):

\( v_1 = \sqrt{\frac{G \cdot M}{R}}  \)

Was bei der Erde bedeuten würde: 7,91 km/s.
Das wäre eine (theoretische) Keisbahn mit dem Radius R; also einer Höhe von  Null Metern über der Erdoberfläche. Nehmen wir mal ein realistisches Beispiel: die ISS. Diese fliegt in ungefähr 400 km Höhe. Da kämen wir auf eine Geschwindigkeit von

\(\Large v = \sqrt{\frac{6.6743 \cdot 10^{-11} \cdot 5.9772 \cdot 10^{24}}{6371000 + 400000}} = 7.94 \enspace km/s \\ \)

Weiter draussen z.B. beim Mond ist die Kreisbahngeschwindigkeit kleiner. Da liegt die Kreisbahngeschwindigkeit nämlich so um 1 km/s.

Die Fluchtgeschwindigkeit

Damit ein Körper der Masse m von der Erdoberfläche entweichen kann, benötigt er eine kinetische Energie, die mindestens so groß ist wie seine potentielle Energie:

\( E_{kin} = \frac{m}{2} \cdot v^2 \)

Das Gravitationspotential auf der Erdoberfläche ist:

\( E_{pot} = \int\limits_{-\infty}^{R} G \cdot \frac{m \cdot M}{r^2} dr = G \cdot m \cdot M \cdot \left[ -\frac{1}{r} \right]_{-\infty}^R  =  -G \cdot m \cdot M \cdot \frac{1}{R}\)

Rechnerisch ergibt sich die Fluchtgeschwindigkeit (sog. Zweite kosmische Geschwindigkeit) zu:

\( v_2 = \sqrt{\frac{2 \cdot G \cdot M}{R}}  \)

Was bei der Erde bedeuten würde: 11,2 km/s

Diese Zahl beruht ausschließlich auf der Gravitation der Erde; soll heissen andere Einflüsse wie Erdrotation oder etwaige Swing-By-Manöver könnten diese erforderliche Geschwindigkeit reduzieren – wie etwa bei den Mondflügen oder Voyager Raumsonden…

Siehe auch: https://de.wikipedia.org/wiki/Fluchtgeschwindigkeit_(Raumfahrt)

Ein Schwarzes Loch

Bei einem Schwarzen Loch wäre die Fluchtgeschwindigkeit die Lichtgeschwindigkeit c.  Wenn wir v2 = c setzen ergibt sich:

\( c = \sqrt{\frac{2 \cdot G \cdot M}{R}}  \)

Aufgelöst nach dem Radius R ergibt sich:

\( R = \frac{2 \cdot G \cdot M}{c^2} \)

Bei einem solchen Radius könnte also kein Licht entkommen; deshalb werden solche Objekte “Schwarze Löcher” genannt. Bei einem kleineren Radius wäre die Fluchtgeschwindigkeit größer als die Lichtgeschwindigkeit; bei einem größeren Radius wäre die Fluchtgeschwindigkeit kleiner als die Lichtgeschwindigkeit. Man nennt diesen Radius den “Schwarzschild-Radius” oder auch den Ereignishorizont.

Genaugenommen müsste man hier die Gleichungen der Allgemeinen Relativitätstheorie (ART) verwenden, da wir hier mit Sicherheit relativistische Effekte wegen der starken Raumkrümmung hätten. Interessanterweise ist die Formel für den Ereignishorizont (Schwarzschild-Radius) aber bei der ART die gleiche wie hier in der “Milchmädchenrechnung”.

 

Physik: Teilreflektion

dkracht

Gehört zu: Physik, Quantenmechanik

Teilreflektion

Die Teilreflektion von Licht an einer Oberfläche hat schon Isaac Newton, der ja von einer Teilchennatur des Lichtes ausging, beschäftigt. Dies ist eines der Paradebeispiele der Quantenmechanik, die ja Aufenthaltswahrscheinlichkeiten für Teilchen ausrechnen will.

Wenn ein monochromatischer Lichtstrahl auf eine Glasplatte scheint, haben wir das Phänomen der Teilreflektion.

Das Ereignis “Reflektion eines Photons an der Grenzschicht Luft/Glas”  habe die Wahrscheinlichkeit von 4% = 4/100 = 1/25. Die Wellenfunktion dieses Ereignisses wäre also ein Vektor der Länge Sqrt{1/25} = 1/5 = 0.2.

Die Drehung des Vektors wäre proportional der Zeit, die das Licht braucht um den Weg zurückzulegen. Wenn wir die Teilreflektion an der dünnen Glasschicht betrachten, spielt nur die Differenz der Laufzeiten eine Rolle, wenn wir die Differenz der Drehwinkel bestimmen wollen..

So bekommen wir gute Beispiele an denen sich Auswirkungen der Quantenphysik in alltälichen Phänomenen demonstieren lassen.

 

 

Astronomie: Kreisbahn – Zentrifugalkraft – Zentripedalkraft – Drehimpuls

dkracht

Drehimpuls gehört zu: Astronomie, Physik, Himmelsmechanik
Siehe auch Keplersche Gesetze, Sonnensystem, Gravitation
Benutzt: WordPress-Plugin Latex

Zentrifugalkraft in einer Kreisbahn

Wenn eine Masse m (z.B. Planet) eine Kreisbahn mit dem Radius r beschreibt, so muss aus Sicht des Planeten eine Kraft in Richtung vom Mittelpunkt der Kreisbahn weg wirken:

\( F = \frac{m \cdot v^2}{r} \)

Diese Kraft nennt man “Zentrifugalkraft”. Das Bezugssystem des auf einer Kreisbahn befindlichen Planeten ist kein Inertialsystem. Die Zentrifugalkraft ist eine “Trägheitskraft” (auch Scheinkraft genannt).

Die Kreisbahn kommt dadurch zustande, dass eine Kraft gleicher Größe in entgegengesetzter Richtung (Zentripedalkraft genannt) wirkt. Im Sonnensystem wirkt die Anziehungskraft des Zentralkörpers Sonne (Graviationskraft) als Zentripedalkraft; man hat also:

\(\frac{m \cdot v^2}{2} = G \cdot \frac{m \cdot M}{r^2}\)

Für die Kreisbahngeschwindigkeit im Sonnensystem gilt also:

\( v = \sqrt{2 \cdot G \cdot M} \cdot \frac{1}{r} \)

Dies ist auch ein Ausgangspunkt der Forschungen von Vera Rubin (1928-2016), die die Rotationsgeschwindigkeit in Galaxien bei unterschiedlichen Abständen vom Zentrum untersucht hat und dadurch die Existenz von sog. Schwarzer Materie bekräftigtigen konnte.

Mit den Mitteln der Vektoralgebra ausgedrückt ergibt sich die Bahngeschwindigkeit bei einer Kreisbewegung zu:

\( \vec{v} = \vec{\omega} \times \vec{r} \\ \)

Definition des Drehimpulses

Klaro: Drehimpuls ist Winkelgeschwindigkeit x Trägheitsmoment.

Da erhebt sich die Frage, was eigentlich ein “Trägheitsmoment” sein soll…

Im Falle einfacher Kreisbahnen von Planeten (Masse) vom Radius R im Sonnensystem folgt aus der allgemeinen Definition des Trägheitsmoments:

\(Trägheitsmoment = Masse \cdot R^2 \)

Damit wäre der Drehimpuls: Winkelgeschwindgkeit x Masse x R Quadrat

Wenn man die Beziehung: Winkelgeschwindigkeit = Bahngeschwindigkeit / R  benutzt, ergibt sich:

\(Drehimpuls = Bahngeschwindigkeit \cdot Masse \cdot R \)

Drehimpuls und die Keplerschen Gestze

Wenn der Drehimpuls eine Erhaltungsgröße ist, folgt aus obiger Gleichung sofort das 2. Keplersche Gesetz.

Beispiele der Erhaltung des Drehimpulses

Wir alle kennen das Beispiel der Pirouette einer Eistänzerin. Wenn die Arme angezogen werden, verringert sich das Trägheitsmoment und die Winkelgeschwindigkeitvsteigt an, da der Drehimplus erhalten bleibt.

 

Physik: Relativitätstheorie, Raum-Zeit-Diagramme, Lorenz-Transformation, Minkowski-Metrik und Eigenzeit

dkracht

Gehört zu: Physik
Siehe auch: Kosmologie, Tensoren, Lineare Algebra, Metrik, Allgemeine Relativitätstheorie, Quantenfeldtheorie, Schwarzes Loch
Benutzt: WordPress-Plugin Latex, Grafiken von Github, Grafiken von Wikipedia

Stand: 01.11.2022  (Vierer-Vektor, Minkowski-Metrik ausführlicher, Weltlinie, Eigenzeit, Loedel, Lorentz-Faktor)

Überschneidungen mit: Relativitätstheorie

Was ist mit “Relativität” gemeint?

Der Begriff der “Relativität” von physikalischen Vorgängen dreht sich darum, dass ein und dieselbe Beobachtung von verschiedenen Beobachtern in verschiedenen Koordinatensystemen gemacht wird. Bei den oben genannten “physikalischen Vorgängen” handelt es sich um die Messung physikalischer Größen wie:

  • Zeit
  • Ort
  • Geschwindigkeit
  • Impuls
  • Beschleunigung
  • Kinetischen Energie
  • Elektromagnetische Kaft
  • Maxwell-Gleichungen
  • …

Dabei könnten zwei Beobachter immer zu übereinstimmenden Ergebnissen kommen (so etwas nennt man dann “invariant”) oder es ergeben sich manchmal unterschiedliche Ergebnisse (“variant”). Im letzteren Fall kommt es also darauf an, welcher Beobachter diese Messung gemacht hat. Somit sind die Ergebnisse also “relativ” zu einem bestimmten Beobachter zu sehen.

Im Falle einer solchen Relativität möchte man die Messergebnisse zwischen Beobachtern formelmäßig “transformieren” können.
Dafür betrachten wir zunächstmal den einfachen Fall, dass sich die Beobachter, gleichförmig und gradlinig zu einander bewegen, also ohne Beschleunigung. Solche Beobachter bzw. deren Koordinatensysteme (Ort und Zeit) nennen wir “Inertialsysteme“.
Ein Beobachter beobachtet Ereignisse, denen er jeweils Ort und Zeit zuordnet.

Raum-Zeit-Diagramm

Solche Ereignisse kann man sich als Punkte in einem sog. Raum-Zeit-Diagramm veranschaulichen, wo die auf der einen Achse die drei Raum-Dimensionen x, y, z auf eine Dimension vereinfacht werden: x. Es bleibt als zweite Achse die Darstellung der Zeit, wobei es sich später als elegant erweisen wird, statt der “echten” Zeit das Produkt aus Lichtgeschwindigkeit und der Zeit, also c · t abzutragen.

Ein Minkowski-Diagramm ist eine ganz einfache grafische Darstellung, nämlich ein rechtwinkliges zweidimensionales Koordinatensystem mit einer Zeitachse und einer Raumachse (also der dreidimensionale Raum auf eine Dimension vereinfacht). Ein Punkt im Minkowski-Diagram wird auch Ereignis genannt, denn der Punkt beschreibt Ort und Zeit. Die Bewegung eines Punktes ist eine Linie im Raum-Zeit-Diagramm und wird seine Weltlinie genannt.

Punkte, die sich gleichförmig und gradlinig bewegen, haben dann als Weltlinie eine Gerade im Raum-Zeit-Diagramm.

Abbildung 1: Minkowski-Diagramm: Weltlinie eines Photons (Github: Minkowski_Diagram_Photon.svg)

Weltlinie eines Photons

Die Weltlinien von Teilchen mit konstanter Geschwindigkeit sind Geraden im Minkowski-Diagramm. Üblicherweise wählt man die Einheiten auf den Achsen so, dass die Weltlinien von Licht (Photonen) eine Steigung von 45 Grad haben.

Mit so einem Raum-Zeit-Diagramm stellen wir also einen 2-dimensionalen Vektorraum dar und suchen nach Transformationen, die Koordinaten eines Punktes (Ereigniss genannt) von einem Koordinatensystem in ein anderes transformieren. Da es sich bei den Koordinatensystemen um Intertialsystem handeln soll, könnten wir vermuten, dass die Transformationen auch ganz einfache sind z.B. Linerare Transformationen, die dann als Matrix dargestellt werden könnten.

Relativität bei Gallileo

Bei Galileo (1564-1642) sind die die physikalischen Gesetze, speziell die Bewegungsgleichungen, identisch in allen Inertialsystemen. Es gibt kein bevorzugtes System, was etwa “in Ruhe” wäre. Jede Bewegung muss relativ zu einem Bezugspunkt gemessen werden.

Speziell für Geschwindigkeiten gilt nach Gallileo das auch intuitiv einleuchtende “Additionsgesetz” d.h. wenn ein Beobachter in seinem System ein Objekt mit der Geschwindigkeit v1 misst, dann wird ein anderer Beobachter, der sich relativ zum ersten Beobachter mit der Geschwindigkeit v bewegt, die Geschwindigkeit desselben Objekts zu v2 = v1 + v messen. Wobei da noch die Richtungen berücksichtigt werden müssen, also: \( \vec{v_2} = \vec{v_1} + \vec{v} \)

Auch die Lichtgeschwindigkeit wäre in unterschiedlichen Inertialsystemen unterschiedlich.

Die Galilieo-Transformationsgleichungen wären demnach:

\(  \tilde{t} = t \\ \tilde{x} = -v \cdot t + x \\ \)

Was als Galileo-Transformationsmatrix ergibt:

\( F = \left[ \begin{array}{rr} 1 & 0 \\  -v & 1 \\  \end{array} \right] \\ B = \left[ \begin{array}{rr} 1 & 0 \\  v & 1 \\  \end{array} \right] \)

Wobei F (=foreward) und B (=backward) wieder die Identität ergeben.

Youtube Video eigenchris 103d: https://youtu.be/ndjiLM5L-1s

Abbildung 2: Galilio-Transformation (Github: Gallileo.svg)

Gallilieo.svg

Gallileo/Newton-Transformation (blau -> rot)

Bei der Koordinatentransformation nach Gallileo/Newton verschiebt sich “nur” die x-Achse, die Zeit (t) ist in jedem bewegten Inertialsystem gleich. Deswegen würde jede Geschwindigkeit (also auch die Lichtgeschwindigkeit) verändert.

Lorentz & Co.

Die sog. Lorentz-Transformationen entstanden nach 1892 um zunächst die damals vorherrschende Äthertheorie in Einklang mit den Ergebnissen des Michelson-Morley-Experiments zu bringen. (Albert A. Michelson 1881 in Potsdam). Die Lorentz-Transformationen wurden erst 1905 von Heny Poicaré (1854-1912)  so formuliert, wie wir sie heute kennen:

\(  c \cdot \tilde{t} = \gamma (ct – \beta x) \\ \tilde{x} = \gamma ( -\beta c t + x) \)

wobei \( \beta = \frac{v}{c}  \) und \( \gamma = \frac{1}{\sqrt{1-\beta^2}} \)

Wobei diese Faktoren so bestimmt sind, dass die Lichtgeschwindigkeit in allen Intertialsystemen gleich ist.

Als Lorentz-Transformationsmatrix ergibt sich:

\( F = \gamma \left[ \begin{array}{rr} 1 & -\beta \\  -\beta & 1 \\  \end{array} \right] \\ B = \gamma \left[ \begin{array}{rr} 1 & +\beta \\  +\beta & 1 \\  \end{array} \right] \)

Youtube Video eigenchris 104b: https://youtu.be/240YGZmV1b0

Abblidung 3: Lorentz-Transformation (Github: Lorentz.svg)

Lorentz Transformation

Lorentz-Transformation (blau -> rot)

Bei der Lorentz-Transformation werden beide Achsen in Richtung auf die Diagonale gedreht. Dadurch werden die ursprünglichen Quadrate zu Rhomben und die Lichtgeschwindigkeit beibt gleich (die Diagonale). Damit bleibt die Skalierung (also die Achsenteilungen) bei der Lozenz-Transformation so, dass die Flächen der Rhomben gleich den Flächen der ursprünglichen Quadrate sind. Für diese Skalierung sorgt der sog. Lorentz-Faktor γ (siehe oben).

Wenn man in so einem Minkowski-Diagramm zwei Intertialsysteme darstellen will, ist das eine rechtwinklig (chartesisch) und die Achsen des anderen sind gemäß Lorentz-Transformation schief dazu – das stört bei Manchen das ästetische Empfinden. Deshalb greift man in so einem Fall auch manchmal zu einer Variante des Minkowsiki-Diagramms, dem Loedel-Minkowsik-Diagramm (nach Ernesto Palumbo Loedel 1901-1962).

Auch der Begriff der Gleichzeitigkeit wird relativ (https://en.wikipedia.org/wiki/Relativity_of_simultaneity)

Abbildung 4: Gleichzeitigkeit (Wikipedia: https://en.wikipedia.org/wiki/Relativity_of_simultaneity#/media/File:Relativity_of_Simultaneity_Animation.gif)
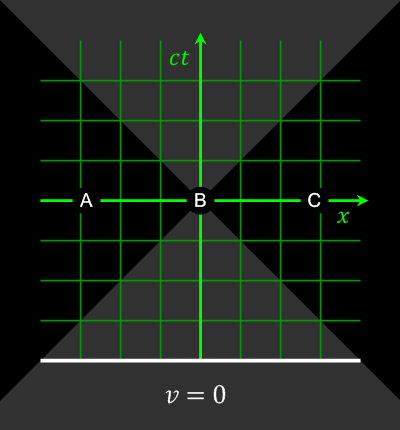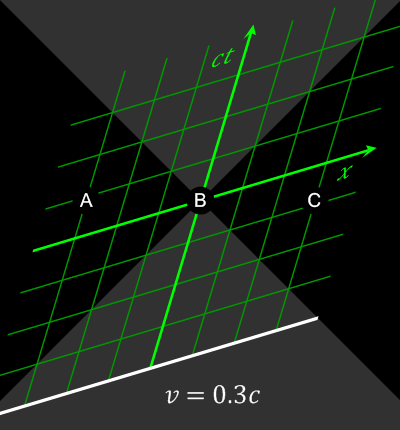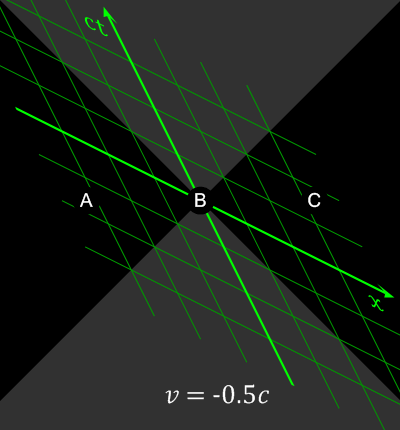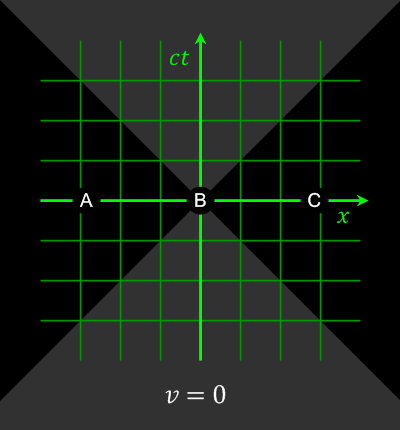
Relativity of Simultaneity (Copyright: Wikipedia)

Bei Ereignissen, die raumartig (s.u.) getrennt sind (|x| > ct) kann durch eine Lorentz-Transformation die Gleichzeitigkeit und damit die Kausalität relativiert werden.

SRT Einsteins Spezielle Relativitätstheorie

Dazu habe ich einen eigenen Blog-Artikel geschrieben: Spezielle Relativitätstheorie

SRT Minkowski-Raum – Minkowski-Metrik – Linienelement

Hermann Minkowski (1864-1909) war Mathematiker und lehrte an den Universitäten Bonn, Königsberg, Zürich und hatte schließlich einen Lehrstuhl in Göttingen. In Zürich war er einer der Lehrer von Albert Einstein.

Auf Minkowski geht die Idee zurück, die Welt (wie Lorenztranformation und Spezielle Relativitätstheorie) als einen nicht-euklidischen vierdimensionalen Raum zu verstehen. Wobei er mit  anschaulichen Bildern (grafischen Darstellungen) anstatt mit schwerer verständlichen Formeln arbeitete.

Zwei Begriffe kommen sofort bei “Minkowski” ins Gespräch:

  • Minkowski-Raum
  • Minkowski-Diagramm

Der Minkowski-Raum ist eine “größere Geschichte”: Ein vierdimensionaler Raum mit einer speziellen Metrik, denn in einem Raum möchte man ja Abstände zweier Punkte messen, Länge von Vektoren, Winkel und Flächen bestimmen.  Eine solche Metrik kann man beispielsweise durch ein Skalarprodukt von Vektoren definieren.
Eine einfache Definition der Metrik im Minkowski-Raum ist gegeben durch (“Linienelement”):

ds²  = c² dt² – (dx² + dy² + dz²)

Soetwas schreiben die Oberspezialisten gern als einen Tensor, auch “metrischer Tensor” genannt:  \( ds^2 = g_{\mu \nu} dx^{\mu} dx^{\nu}\) (bei einem Tensor wird “implizit” summiert.)

Wenn man unser Universum als Minkowski-Raum verstehen wollte, mit einer durch das Linienelement

ds²  = c² dt² – (dx² + dy² + dz²)

definierten Metrik, wäre das ein “flacher” Raum, also nicht gekrümmt (so zu sagen ohne Gravitation).

In so einem Minkowski-Raum, also mit der Minkowski-Metrik, lässt sich die Spezielle Relativitätstheorie (SRT) sehr einfach grafisch darstellen.

Das Linienelement der Minkowski-Metrik

Hermann Minkowski (1864-1909) war ein deutscher Mathematiker, der zeitweise auch Einsteins Lehrer in Zürich war.

Ein Minkowski-Diagramm ist ja relativ locker definiert (s.o.). Da haben wir eben die Zeit als weitere Dimension und beschreiben damit eine Ereignis in der Raumzeit durch einen Punkt mit vier Koordinaten:

Ereignis: e = (t, x, y, z)

Von einem Minkowski-Raum spricht man, wenn man auch noch eine Metrik hat, womit dann Abstände definiert werden. Allerdings wollen wir eine Metrik, die Lorentz-invariant ist; d.h. der Abstand zweier Ereingnisse (Punkte) soll in allen Inertialsystemen, die durch Lorentz-Transformation in einander übergehen, der gleiche sein. Mit einem einfach gedachten Linienelement:

ds²  = c² dt² + dx² + dy² + dz²

funktioniert das leider nicht (kann man ausrechnen).

Als sog. Minkowski-Metrik definiert man stattdessen das Linienelement:

ds²  = c² dt² – (dx² + dy² + dz²)

Die dadurch definierte Metrik ist tatsächlich Lorentz-invariant (kann man ausrechnen). Formal wird diese Minkowski-Metrik definiert durch einen Metrik-Tensor, den sog. Minkowski-Tensor (siehe dort).

So eine Metrik definiert zunächsteinmal die Länge eines Vektors \( \vec{S} = ( x^1, x^2, x^3, x^4 ) \) als:

\( || \vec{S} || = \sqrt{\vec{S} \cdot \vec{S}} = \sqrt{g_{ij} x^i x^j}  \)

Um den Abstand zweier Ereignisse in unserer Raumzeit  s1 = (t1, x1, y1, z1) und s2 = (t2, x2, y2, z2) zu ermitteln, nehmen wir die Länge des Differenz-Vektors:

\(  s^2 = || s_2 – s_1 || =  c^2 (t_2 – t_1)^2 – (x_2 – x_1)^2 – (y_2 – y_1)^2 – (z_2 – z_1)^2  \)

In so einem Minkowski-Raum, also mit der Minkowski-Metrik, lässt sich die Spezielle Relativitätstheorie (SRT) demnach sehr einfach grafisch darstellen eben weil diese Metrik Lorentz-invariant ist.

Man sagt auch: Wenn man unser Universum als Minkowski-Raum verstehen wollte, mit dieser Metrik,  wäre das ein “flacher” Raum, also nicht gekrümmt (so zu sagen ohne Gravitation).

Raumartig, Zeitartig, Lichtartig

Für den Abstand zweier Ereignisse können wir unterscheiden:

  • \( s^2 > 0 \) : Der Abstand wird “zeitartig” genannt – die Ereignisse sind zeitartig getrennt
  • \( s^2 < 0 \) : Der Abstand wird “raumartig” genannt – die Ereignisse sind raumartig getrennt
  • \( s^2 = 0 \) : Der Abstand wird “lichtartig” genannt

Auf eine Raum-Dimension vereinfacht, ist der Minkowski-Abstand: \( s^2 = c^2 t^2 – x^2 \). Damit ist dann:

  • Zeitartiger Abstand: \( x < ct \)
  • Raumartiger Abstand:   \( x > ct \)
  • Lichtartiger Abstand: \( x = ct \)

Abblidung 5: Minkowski-Metrik (Github: Minkowski-02.svg)

Minkowski-02.svg

Kurven als Weltlinie

Die Begriffe “raumartig” (space like) und “zeitartig” (time like) werden auch für Kurven im Minkowski-Diagramm verwendet.
Dabei betrachtet man infenitesimal kleine Kurvenstücke und fragt sich, ob diese als Intervall immer raumartig oder immer zeitartig sind.
Ein wichtiges Thema sind “closed timelike curves”…

Minkowski-Abstand

Man darf sich von der Optik des Minkowski-Diagramms nicht zu vereinfachten Schlüssen verführen lassen. Bei einem Minkowski-Abstand von: \( s^2 = c^2 t^2 – x^2 \) liegen beispielsweise alle Punkte (Ereignisse), die vom Koordinatenursprung den Minkowski-Abstand 1 haben, nicht auf der Kugelschale mit Radius 1, sondern die Menge (ct, x):

\( 1 = {ct}^2 – x^2 \)

Das ist eine Hyperbel im Minkowski-Diagramm. Dort liegen also alle Punkte im ursprünglichen Bezugssystem (ct,x), die eine Abstand 1 vom Koordinatenursprung haben.

Da dieser Anstand invariant ist, liegt dort also auch für jedes Lorenz-transformierte Bezugssystem (ct’, x’) der Punkt auf der transformierten Raum-Achse, der einen Abstand 1 vom Ursprung hat.

Wir müssen also immer daran denken, dass im Minkowski-Raum nicht die vom Diagramm “vorgegaukelte” Euklidische Geometrie gilt, sondern der Minkowski-Abstand.

Abbildung 6: Minkowski-Abstand (Github: hyperbel.svg)

Hyperbel.svg

Minkowski-Metrik

Vierer-Vektoren

Im Raum-Zeit-Diagramm ist ein Punkt ein Ereignis, beschrieben durch seinen Ort im Raum und den Zeitpunkt; man benötigt im dreidimensionalen Raum also 4 Koordinaten (siehe Koordinatensysteme). Man spricht deswegen auch von einem Vierer-Vektor:

\( \vec{S} =  \left[ \begin{array}{c} ct \\\ x \\\ y \\\ z  \end{array} \right] \)

Mit der Vektor-Basis ausgedrückt ist das:
\( \vec{S} = ct \cdot \vec{e_t} +  x \cdot \vec{e_x}  + y \cdot \vec{e_y} + z \cdot \vec{e_z} \\ \)

Entsprechend hätte man Vierer-Geschwindigkeit, Vierer-Impuls, Vierer-Beschleuigung etc. Der springende Punkt bei diesen “Vierer-Vektoren” ist aber nicht die eigentlich triviale Tatsache, dass die Vektoren vier Komponenten haben, sondern die Art und Weise, wie nach der Zeit differenziert wird. Die Zeit-Koordinate (“Koordinatenzeit”) ist ja in jedem Interialsystem eine andere, weshalb für die Vierer-Vektoren die sog. Eigenzeit (engl. proper time, Symbol τ) genommen wird.

Bei einer genaueren Definition des Begriffs “Vier-Vektor” würde man die Invarianz der Vektor-Länge bei Lorenztransformationen fordern. Die Länge eines Vierer-Vektors ergibt sich dabei durch die Metrik.

Siehe auch: http://walter.bislins.ch/blog/index.asp?page=Bewegungsgleichung+der+Speziellen+Relativit%E4tstheorie

Eigenzeit in der Minkowski-Metrik

Als Eigenzeit (Symbol τ) eines bewegten Objekts (entlang einer beliebigen Weltlinie) bezeichnet man die Zeit, die eine “mitbewegte” Uhr  zeigt. Jede Weltlinie hat eine eigene Eigenzeit.
Wir werden sehen: Die Eigenzeit ist die auf einer Weltlinie gemessene Länge in der Minkowski-Metrik und deshalb auch Lorenz-invariant.

Im Gegensatz dazu ist die Zeitkoordinate (auch Koordinatenzeit) eben eine von vier Koordinaten im verwendeten Koordinatensystem und transformiert sich, wenn wir auf ein anderes Koordinatensystem übergehen.

Für den einfachen Fall eines Objektes, dass sich geradlinig mit konstanter Geschwindigkeit \( \vec{v} \) bezüglich unseres Bezugssystems (ct, x) bewegt, ist das ganz einfach. Dann ist die Weltlinie dieses Objekts eine Gerade in unserem Koordinatensystem und wir häten die Bewegung:

\(  x(t) = ||\vec{v}|| \cdot t \)

Wir können an ein solches Objekt dann ein Koordinatensystem (ct’, x’) “anheften”, was wieder ein Intertialsystem wäre. Man spricht vom “mitbewegten” System. Den Zusammenhang liefert die Lorenz-Transformation. Wenn wir jetzt einen Zeitabschnitt von \(\Delta t \) (in unserem Bezugssystem) betrachten, wäre die Frage. welche Zeit im mitbewegten Bezugssystem dann vergeht.

\( \Delta t^{\prime} = \sqrt{1-\frac{||v||^2}{c^2}} \cdot \Delta t \)

Wenn wir nun ein Objekt betrachten, dass sich nicht auf einer Geraden als Weltlinie bewegt, wäre ein mitbewegtes Bezugssystem kein Inertialsystem mehr. Die dort vergangene Zeitspanne von ta bis te, also die Eigenzeit, ergibt sich dann aufintegriert als:

\(  \tau =  \displaystyle\int\limits_{t_a}^{t_e} \sqrt{1-\frac{||v(t)||^2}{c^2}} \, dt \)

Diese Eigenzeit τ würde dann von allen Intertialsystemen aus gesehen gleich sein d.h. Lorenz-invariant.

Euklidische Vektoren

Im klassischen Eukidischen Raum (soll heissen ohne die SRT) haben wir es generell mit 3er-Vektoren zu tun:

Ortsvektor: \( \vec{r} = x \cdot  \vec{e_x} + y \cdot \vec{e_y} + z \cdot \vec{e_z} \)

Geschwindigkeit: \( \vec{u} = \frac{d \vec{r}}{d t} \)

Impuls: \( \vec{p} = m \cdot \vec{u} \)

Beschleunigung: \( \vec{a} = \frac{d^2 \vec{r}}{d t^2} = \frac{d \vec{u}}{d t} \)

Kraft: \( \vec{f} = \frac{d \vec{p}}{d t} = m \cdot \vec{a} \)

Minkowski-Vektoren

Wenn wir das Obige nun nach SRT und in beliebigen Inertialsystemen betrachten wollen, haben wir gleich ein Problem mit den Ableitungen nach der Zeit. In jedem Inertialsystem verläuft die Zeit (auch Koordinatenzeit genannt)  anders; d.h. die o.g. Größen sind nicht mehr Lorenz-invariant.

Lorenz-invariant sind zunächst:

  1. Die Lichtgeschwindigkeit: c
  2. Der Minkowski-Abstand zweier Ereignisse: \( S = c \cdot (t_2 – t_1) – (x_2 – x_1)^2 – (y_2 – y_1)^2 – (z_2 -z_1)^2   \)

Einerseits ist die Zeit eine Koordinate in der vierdimensionalen Raumzeit, andererseits können wir zeitliche Abstände zwischen zwei Ereignissen messen.

Anstelle der Zeit (Koordinatenzeit), die in allen Inertialsystem verschieden sein kann, definieren wir eine sog. Eigenzeit τ, die invariant sein soll. Danach können die das differenzieren und kämen zu invarianten Größen….

Bei den Minkowski-Vektióren (Vierervektoren) gehen wir aus vom Ortsvektor, der die Bewegung eines Massepunkts m in seiner Eigenzeit beschreibt (Weltlinie):

\( \vec{S} = ct \cdot \vec{e_t} +  x \cdot \vec{e_x}  + y \cdot \vec{e_y} + z \cdot \vec{e_z} \\ \)

Durch Differenzieren nach der Eigenzeit kommen wir dann zu:

Vierer-Geschwindigkeit: \( \vec{U} = \Large \frac{d\vec{S}}{d\tau} \)

Vierter-Impuls: \( \vec{P} = m \cdot \vec{U}  \)

Vierer-Beschleunigung: \( \vec{A} = \Large \frac{d^2\vec{S}}{d\tau^2} = \frac{d\vec{U}}{d\tau} \)

Vierer-Kraft: \( \vec{F} = \Large \frac{d\vec{P}}{d\tau} = m \cdot \vec{A} \)

Wie differenziere ich nun nach der Eigenzeit?

Vierer-Geschwindigkeit:

\( \Large \vec{U} =\frac{d\vec{S}}{d\tau} = \frac{d}{d\tau}(   ct \cdot \vec{e}_t +  x \cdot \vec{e}_x  + y \cdot \vec{e}_y + z \cdot \vec{e}_z    ) \)

In einem Inertialsystem sind die Basisvektoren konstant; d.h. die Ableitungen auch nach τ sind Null. Damit vereinfacht sich die Produktregel und wir erhalten:

\( \Large \vec{U} = \frac{d\vec{S}}{d\tau} = c \frac{dt}{d\tau} \vec{e}_t + \frac{dx}{d\tau} \vec{e}_x + \frac{dy}{d\tau} \vec{e}_y + \frac{dz}{d\tau} \vec{e}_z \)

 

 

 

Physik: Quantenmechanik

dkracht

Gehört zu: Physik
Siehe auch: Kosmologie, Teilchenphysik, Von Pythagoras bis Einstein, Lineare Algebra, Bra-Ket-Notation
Benötigt: WordPress Latex-Plugin, Fotos von Wikipedia

Stand: 08.04.2022   (h quer, Strahlungsspektrum Grafik)

Prinzipien der Quantenmechanik

Im Jahr 1900 formulierte Max Planck (1858-1947) sein Strahlungsgesetz und seine Quantenhypothese. Erst um 1925 entwickelte sich daraus eine Quantentheorie/Quantenmechanik, die die physikalische Systeme im Kleinen (z.B. Elementarteilchen, Atome,…). gut beschreibt. Wesentliche Punkte sind:

Verständnis der Quantenmechanik

Die Formalismen der Quantenmechanik dienen lediglich als Mittel zur Vorhersage der relativen Häufigkeit von Messergebnissen; diese werden als die einzigen Elemente der Realität angesehen.

Eine wirkliches “inneres” Verständnis der Quantenmechanik ist heute noch nicht vorhanden. Man kann zwar damit “rechnen”, weiss aber eigentlich nicht, was da “im Inneren” passiert. Link: https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics

Zitat Richard Feynman (1918-1988): “I think I can safely say that nobody understands quantum mechanics.”
Link: https://www.researchgate.net/post/I_think_I_can_safely_say_that_nobody_understands_quantum_mechanics_R_Feynman_If_that_statement_is_true_how_can_we_know_if_QM_is_true

Abbildung 1: Flammarion Holzschnitt (Wikipedia: FlammarionWoodcut.jpg)

Flammarion Holzschnitt (Wikipedia)

Das Plancksche Strahlungsgesetz

Bestimmte phsikalische Größen kommen nur in ganzzahligen Vielfachen eines “kleinsten” Wertes vor. Das nennt man Quantelung. Der Ursprung dieser Idee “Quantenhypothese” soll das Plancksche Strahlungsgesetz sein.

Max Planck (1858-1947) beschäftigte sich mit die Strahlung eines sog. “Schwarzen Strahlers”. Speziell ging es ihm darum, wie sich in Abhängigkeit von der Temperatur die abgestrahlte Energie über die Wellenlängen hin verteilt. Man kannte damals schon die abgestrahlte Gesamt-Energie (Stefan-Boltzmann-Gesetz) und auch die Wellenlänge bei der das Maximum an Energie abgestrahlt wird (Wiensches Verschiebungsgesetz). Die früheren Formeln zur Verteilung über die Wellenlängen z.B. von Rayleigh-Jeans waren nur Teilerfolge, da sie in der sog. “Ultraviolettkatastrophe” endeten.

Max Planck konnte im Jahre 1900 ein Strahlungsgesetz entwickeln, das zeigt welche Strahlungsenergie ein “Schwarzer Strahler” einer bestimmten Temperatur (T) in Anhängigkeit von der Wellenlänge (oder Frequenz “ν”) der Strahlung aussendet. Plancks Strahlungsgesetz ist eigentlich nur eine Formel wie viele andere in der Physik auch, die endlich die Verteilung der Strahlungsenergie in Abhängigkeit von der Wellenlänge/Frequenz der Strahlung “richtig” darstellt.

\( \Large \frac{8 \cdot \pi  \cdot h \cdot \nu^3}{c^3} \cdot \frac{1}{e^\frac{h \nu}{k T} – 1}\)

Abbildung 2: Verteilung der Stahlungsenergie

Planksches Strahlungsspektrum (Wikipedia)

Wir sehen, dass je nach Temperatur, das Maxium der Strahlung bei einer anderen Wellenlänge (einer anderen Farbe) liegt.

Das nach Wilhelm Wien (1864-1928) benannte Wiensche Verschiebungsgesetz besagt, dass  ein Schwarzer Körper der absoluten Temperatur T die intensivste Strahlung bei einer Wellenlänge λmax abgibt, die umgekehrt proportional zu seiner Temperatur ist; als Formel:

\( \lambda_{max} = 2897,8 \mu m \cdot \frac{1}{T}\)   (T in Kelvin)

Aus der Farbe eines thermischen Strahlers kann so auf seine Temperatur zurückgeschlossen werden. Zum Beispiel teilt man die Sterne gemäß ihrer Farbe in Spektralklassen ein, denen eine Temperaturskala entspricht.

In Plancks Formel kommt eine vom ihm so genannte “Hilfskonstante” h vor, die später als das legendäre Plancksche Wirkungsquantum interpretiert wurde. Die physikalische Größe “Wirkung” bezeichnet eine Energie (Joule), die in einer bestimmten Zeit  (Sekunden) etwas “bewirkt”. Die Planck’sch Hilfskonstante ist:

h = 6,626069 ⋅ 10-34 J ⋅ s

h = 6,626   069 ⋅ 10 − 34   J ⋅ s

Dieses Youtube-Video von Rene Matzdorf  an der Uni Kassel versucht, die Herleitung der Planck’schen Formel (Strahlungsgesetz) über die Strahlung den schwarzen Körpern, sog. Hohlraumstrahlung und darin existierenden stehenden Wellen (Hohlraum-Resonator) herzuleiten:

Der Zusammenhang ist für mich nicht so leicht nachvollziehbar. Aber man muss das Placksche Schrahlungsgesetz ja überhaupt nicht “herleiten” – hat Newton bei seiner Gravitationstheorie ja auch nicht gemacht.

In physikalischen Formeln wird auch häufig ein sog. “Reduziertes Plancksches Wirkungsquantum” mit dem Symbol “h quer” verwendet. Es ist definiert als: \( \hbar = \frac{h}{2\pi} \)

Quelle: http://www.quantenwelt.de/quantenmechanik/historisch/schwarze_korper.html

Plancks Quantenhypothese

Häufig hört man, dass aus Plancks Formel angeblich die Aussendung der Energie in sog. Quanten (ganzzahlige Vielfache  von h mal ν) folgt. Das kann man aber aus der Formel selbst überhaupt nicht ableiten. Vielmehr ist es so, dass Planck (angeblich) auf diese Formel kam indem er elektromagnetische Strahlung (das Licht) als Teilchen modellierte, die sich wie ein Gas verhalten sollten. Die unterschiedlichen Geschwindigkeiten solcher Teilchen modelliert Planck als unterschiedliche Wellenlängen der Strahlung…

Ein solches Teilchen sollte eine von der Frequenz seiner Strahlung abhängige Energie haben. Das ist die zentrale Formel (Quantenhypothese) von Planck:   \(E = h \cdot \nu \)

Die Formeln für das Strahlungsgesetz hat Planck zunächst durch Probieren herausgefunden und dann später eine Herleitung auf Basis seiner Quantenhypothese gefunden. Planck glaubte jedoch damals noch nicht an eine allgemeine Quantelung, diese war nur eine Annahme, um die Theorie in Einklang mit den Messungen bringen zu können.

Später versuchte Planck sein Strahlungsgesetz nicht durch eine “Hohlraumstrahlung” sonden durch Atome als Oszillator zu interpretieen.

Der Photoelektrische Effekt

Einfacher für mich ist die Erklärung mit dem photoelektrischen Effekt. Einstein (1879-1955) benutzte gequantelte Photonen mit der Energie \(E = h \cdot \nu \), um den photoelektrischen Effekt zu erklären.

Nach Einstein nimmt die Intensität von Licht dadurch zu, dass mehr Photonen mit der gleichen Energie pro Zeiteinheit abgestrahlt werden. Der photoelektrische Effekt wirkt aber erst dann, wenn das einzelne Photon die erforderliche Energie hat, um Elektronen aus dem Basismaterial herauszulösen. Es ist also nicht eine bestimmte hohe Intensität des Lichts erforderlich, sondern eine bestimmte hohe Frequenz, um die Auslösearbeit zu leisten…

Das Bohrsche Atommodell

Der Erfolg dieser Theorien brachte Niels Bohr (1885-1962) dazu, so eine Quantelung auch für die Enegieniveaus der Elektronen-Orbitale in seinem Atommodell anzunehmen.

Man stellt sich dabei so ein Orbital als eine stehende Welle (s. Schrödinger-Gleichung) vor.

Quantelung

Welche physikalischen Größen sollen den nun “gequantelt” sein; d.h. nur in ganzzahligen Vielfachen einer (kleinen) Elementargröße (=Quanten) vorkommen? Kommt jede physikalische Größe in “Quanten” oder nur bestimmte?

Ich habe in Heidelberg gehört, dass die Quantelung nur für physikalische Größen zutrifft, die konjugiert zu einer periodischen Größe sind. Was immer das heissen mag…

Das Plancksche Wirkungsquantum

Das Plancksche Wirkungsquantum als Naturkonstante wird heute zur Definition der SI-Einheit Kilogramm benutzt.

Im Zusammenhang mit dem Wirkungsquantum spricht man auch von einer einer “Planck-Länge”, einer “Planck-Zeit” etc., denn Planck hatte herausgefunden, dass man aus den Naturkonstanten G, c, h eine ganze Schaar von Einheiten ableiten kann (durch Probieren und Beachten der Dimensionen):

Planck-Länge:

\(  \Large l_p = \sqrt{\frac{\hbar \cdot G}{c^3}} = 6.616 10^{-35}m\\ \)

Was diese Planck-Länge bedeutet, ist zunächst völlig offen. Es ist “nur” eine ausprobierte Formel, die als Dimension eine Länge hat.

Im Zusammenhang mit der Heisenbergschen Unschärferelation versucht man, diesen Planck-Größen eine physikalische Bedeutung beizumessen.

 

 

 

 

Physik

dkracht

Gehört zu: Physik
Siehe auch: Quantenmechanik, Thermodynamik, Elektrodynamik

Stand: 01.10.2022

Physik

Am Rande (neben der Astronomie und der Computerei) beschäftige ich mich auch mit Teilaskepten der Physik.

Klassischerweise teilt man das Gebiet der Physik ein in:

  • Mechanik (Klassiker: Galilleo, Newton,…)
  • Thermodynamik (Wärmelehre) (Dampfmaschinen)
  • Elektrodynamik (Elektrizität, Magnetismus)

Geschrieben habe ich folgende Beiträge:

….

 

Astronomie: Physikalische Größen

dkracht

Gehört zu: Astronomie, Physik
Siehe auch: Scheinbare Helligkeit, Entfernungsbestimmung, Zeitmessung, Thermodynamik, Energie, Elektrisches Feld, Magnetisches Feld

Stand: 21.04.2023

Physikalische Größen: SI-Basiseinheiten

Die französische Akademie der Wissenschaften erhält 1790 von der französischen Nationalversammlung den Auftrag, ein einheitliches System von Maßen und Gewichten zu entwerfen. Sie folgt dabei den Prinzipien, die Grundeinheiten aus naturgegebenen Größen abzuleiten, alle anderen Einheiten darauf zurückzuführen und alle, mit Ausnahme der Zeit, dezimal zu vervielfachen und zu unterteilen. Als Grundeinheiten wurden Meter, Gramm und Sekunde gewählt.

1889 Gründung der Generalkonferenz für Maß und Gewicht (CGPM = Conférence Générale des Poids et Mesures)

Aktuell (im Jahre 2020) sind als sog. SI-Basiseinheiten (französisch Système international d’unités) international definiert:

  1. Meter (m)  – Länge
  2. Sekunde (s) –  Zeit
  3. Kilogramm  (kg) –  Masse
  4. Ampere (A) –  Stromstärke  (1948)
  5. Kelvin (K) –  Temperatur  (1954, 1968)
  6. Mol (mol) –  Stoffmenge  (1971)
  7. Candela (cd)  –  Lichtstärke   (1979)

Länge: Meter

1790: Erste Definition des Meters als zehnmillionster Teil des Erdmeridianquadranten

1960 wurde dieses “Urmeter” abgelöst durch eine neue Definition des Meters als Vielfaches der Wellenlänge eines Kyrpton-Lasers zu definieren.
Die Wellenlänge einer elektromagnetischen Strahlung, die vom Kryptonisotop 86Kr ausgestrahlt wird, wurde 1960 als Grundlage für die Definition des Meters gewählt.  Ein Meter wurde als das 1.650.763,73fache der Wellenlänge der vom Nuklid 86Kr beim Übergang vom 5d5 in den 2pl0-Zustand ausgesandten und sich im Vakuum ausbreitenden Strahlung definiert.

1983 hat die  17. Generalkonferenz für Maß und Gewicht das Verhältnis zwischen Lichtgeschwindigkeit und Meterdefinition umgekehrt.
Dabei wurde die Lichtgeschwindigkeit als Naturkonstante definiert zu 299 792 458 m/s und das Meter definiert als “Die Strecke, die Licht im Vakuum während der Zeit von 1/299 792 458 Sekunden zurücklegt”.

Zeit: Sekunde

1790:  Erste Definition der Sekunde als 1/86 400ster Teil des mittleren Sonnentages

1967 hat man der Sekunde eine atomphysikalische Definition gegeben: “Die Sekunde ist das 9 192 631 770-fache der Periodendauer der dem Übergang zwischen den beiden Hyperfeinstrukturniveaus des Grundzustandes von Atomen des Nuklids Cs-133 entsprechenden Strahlung.”

Masse: Gramm / Kilogramm

Ursprünglich sollte ein Kilogramm der Masse von einem Liter Wasser entsprechen.

1790: Erste Definition des Gramms als Gewicht, später als Masse von 1 cm3 reinem Wasser bei 4 °C und einem Druck von 760 mm Quecksilbersäule

1890: Das Urkilogramm als ein Zylinder aus Platin-Iridium

2019: 20. Mai 2019: Mit Hilfe einer Siliziumkugel wird die Masse eines Si-Atoms bestimmt und damit die Größe des Planckschen Wirkungsquantums h. Danach dreht man den Spieß um und legt die Größe des Planckschen Wirkungsaunatums als Naturkonstante so wie gerade gemessen fest (so wie es früher schon mit der Lichtgeschwindigkeit geschah). Nun kann man definieren:  Das Kilogramm, Einheitenzeichen kg, ist die SI-Einheit der Masse. Es ist definiert, indem für die Planck-Konstante h der Zahlenwert 6.62607015*10–34 Js festgelegt wird, Wobei ja  \( 1 Js =  1 \frac{kg \cdot m^2}{s} \) ist, wobei der Meter und die Sekunde unabhängig als SI-Einheiten definiert sind.

Stromstärke: Ampere

1898 wurde 1 Ampere im „Gesetz, betreffend die elektrischen Maßeinheiten des Deutschen Kaiserreichs” als die Stärke desjenigen Stromes definiert, der aus einer wässrigen Silbernitrat-Lösung mittels Elektrolyse in einer Sekunde 1,118 mg Silber abscheidet. Das so definierte Ampere ist später als internationales Ampere bezeichnet worden; das mit den restlichen Basiseinheiten kompatible dagegen als absolutes Ampere.

1948 wurde das Ampere über die Lorentzkraft zweier Leiter aufeinander definiert: 1 A ist die Stärke des zeitlich konstanten elektrischen Stromes, der im Vakuum zwischen zwei parallelen, unendlich langen, geraden Leitern mit vernachlässigbar kleinem, kreisförmigem Querschnitt und dem Abstand von 1 m zwischen diesen Leitern eine Kraft von 2 · 10−7 Newton pro Meter Leiterlänge hervorrufen würde.

2019 Auf der 26. Generalkonferenz für Maß und Gewicht beschlossen, das Ampere und andere SI-Basiseinheiten mit Wirkung zum 20. Mai 2019 neu zu definieren. Mit dieser Neudefinition des Internationalen Einheitensystems basiert das Ampere auf der Elementarladung, der ein fester Zahlenwert zugewiesen wurde: 1.602176634 * 10–19  C. Seitdem hängt die Definition des Amperes nur mehr von der Definition der Sekunde ab, nicht mehr jedoch vom Meter und vom Kilogramm.

Temperatur: Kelvin

1948 wurde durch die 9. Generalkonferenz für Maß und Gewicht (CGPM) festgelegt, dass eine absolute thermodynamische Skala den Tripelpunkt des Wassers als einzigen fundamentalen Fixpunkt haben sollte. Vor allem die starke Abhängigkeit des Siedepunkts vom Luftdruck hatte die Temperatureichung über die bisherigen Fixpunkte schwierig gemacht. Der Tripelpunkt hingegen war leicht und eindeutig reproduzierbar.

1954 wurde das Kelvin von der CGPM in der bis zum 19. Mai 2019 gültigen Form definiert und zur Basiseinheit erklärt. Dadurch bekam zugleich das Grad Celsius eine neue Definition. Die Bezeichnung war zunächst „Grad Kelvin (°K)“ und wurde 1967 auf „Kelvin (K)“ geändert. Die Definition lautete seitdem: „Das Kelvin, die Einheit der thermodynamischen Temperatur, ist der 273,16-te Teil der thermodynamischen Temperatur des Tripelpunktes des Wassers.“.

2019: Anbindung an die thermische Energie: Die thermodynamische Temperatur eines Systems ist direkt proportional zu der mittleren kinetische Energie der ungeordneten Bewegung seiner mikroskopischen Teilchen. Die thermische Energie (Formelzeichen: Q) eines Systems ist Teil der sog. “Inneren Energie” (Formelzeichen: U) des Systems.

Die Boltzmann-Konstante ist der Proportionalitätsfaktor  (1.380649 * 10–23 Joule/Kelvin). Solange die Einheiten von Energie (Joule) und Temperatur (Kelvin) unabhängig voneinander definiert waren, musste die Boltzmann-Konstante experimentell bestimmt werden. Diese Messungen wurden im Laufe der Zeit immer präziser und erreichten schließlich die Genauigkeit der Realisierung des Kelvin über den Tripelpunkt des Wassers. Damit war die Existenz zweier konkurrierender Definitionen nicht mehr zu rechtfertigen. Der Boltzmann-Konstanten wurde ein fester Wert in der Einheit J/K zugewiesen und das Kelvin dadurch direkt an das Joule gekoppelt. Der Wert der Boltzmann-Konstanten, die seitdem ein nur durch Konvention festgelegter Skalierungsfaktor ist, wurde so gewählt, dass das neue Kelvin möglichst genau mit dem alten übereinstimmte. Diese Änderung trat mit der Revision des Internationalen Einheitensystems am 20. Mai 2019 in Kraft.

Stoffmenge: Mol

Die Maßeinheit der Stoffmenge ist das Mol, eine SI-Basiseinheit.

1971: Ein Mol ist die Menge einer Substanz, in der gleichviel Moleküle sind, wie in 12 g von Kohlenstoff 12C.

2019: Eine Stoffmenge von 1 Mol (= 1 mol) enthält die durch die Avogadro-Konstante (NA = 6.02214076 * 1023 mol−1) festgelegte Teilchenzahl. Die Avogadro-Konstante ist der Proportionalitätsfaktor zwischen der Stoffmenge und der Teilchenzahl N(X). Teilchen können hier Atome, Ionen, Moleküle oder auch Elektronen sein. Formelzeichen und Teilchenart X werden zusammen als nX oder n(X) angegeben.

Lichtstärke: Candela

Für die Messung der Himmelshelligkeit ist die Lichtstärke (intensity) gemessen in Candela interessant. Wobei die SI-Definition besagt:

Eine Lichtquelle hat die Lichtstärke Iv = 1 cd, wenn sie monochromatisches Licht der Frequenz 540 x 1012 Hertz (555 nm) aussendet und dabei in einen Raumwinkel von 1 sr (Steradiant) eine Leistung von 1/683 Watt abgibt.

Von Candela abgeleitete Einheiten:

  • Lichtstrom  Φv , gemessen in Lumen (lm): Eine Lichtquelle der Lichtstärke Iv = 1 cd strahlt in einen Raumwinkel von 1 sr einen Lichtstrom von 1 lm (Lumen) ab. Also lm = cd sr
  • Leuchtdichte  Lv , gemessen in Candela pro Qudratmeter  (cd m-2 oder lm m-2 sr-1)
  • Beleuchtungsstärke E, gemessen in Lux (lx):  Lichtstrom pro m². Also lx = lm m-2

Bei all diesen Größen handelt es sich darum, wie die Licht-Intensität vom menschliche Auge als Helligkeiten etc. wahrgenommen wird. Für die Beleuchtungsindustrie ist es wichtig, so etwas zu messen.
Physikalisch ist aber nicht die menschlich wahrgenommene Licht-Intensität sondern die Energieabgabe im gesamten Spektralbereich (also über alle Wellenlängen) relevant. Beispielsweise wird die Intensität einer Strahlungsquelle in Joule pro Sekunde  (Watt) gemessen. Dafür benötigt man keine solchen Maßeinheiten wie Candela etc.

Abgeleitete SI-Einheiten

Als sog. abgeleitete SI-Einheiten (mit eigenem Namen) sind festgelegt:

  • Kraft: Newton:  1 N = 1 kg m/s2
  • Energie: Joule = 1 J = 1 N m = 1 kg m2 / s2
  • Leistung: Watt: 1 W = 1 J/s = 1 kg m2 / s3
  • Elektrische Ladung: Coulomb: 1 C = 1 A s
  • Elektrische Spannung: Volt: 1 V = 1 W / A = 1 kg m2 / (A * s3)
  • Magnetische Flußdichte: Tesla: 1 T = 1 N / A m = 1 kg / (A * s2)
  • Lichtstrom: Lumen: 1 lm = 1 cd * sterad
  • …