Wissen

Physik: Wellengleichung

dkracht

Gehört zu: Physik
Siehe auch: Von Phythagoras bis Einstein, Schroedinger

Stand: 27.9.2024

Die Wellengleichung von D’Alembert

Die Wellengleichung, auch D’Alembert-Gleichung nach Jean-Baptiste le Rond d’Alembert (1717-1783), bestimmt die Ausbreitung von Wellen wie etwa Schall oder Licht.

Wenn das Medium oder Vakuum die Welle nur durchleitet und nicht selbst Wellen erzeugt, handelt es sich genauer um die homogene Wellengleichung, die lineare partielle Differentialgleichung zweiter Ordnung

\(\Large  \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} – \sum \limits_{i=1}^{n} \frac{\partial^2 u}{\partial x^2_i} = 0 \)

für eine reelle Funktion u (t, x1, x2,…,xn) der Raumzeit.

Hierbei bedeutet u die Auslenkung der Welle zur Zeit t am Ort x=(x1, x2,…,xn) und  n die Dimension des Raumes.
Der Parameter c ist die Ausbreitungsgeschwindigkeit der Welle, also bei Schall (im homogenen und isotropen Medium) die Schallgeschwindigkeit und bei Licht die Lichtgeschwindigkeit.

Die eindimensionale Wellengleichung

Im einfachen Fall nur einer Raumdimension (n=1) bekommen wir als Wellengleichung:

\(\Large  \frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} –  \frac{\partial^2 u}{\partial x^2} = 0 \\\)

Und als Lösung  für harmonische Schwingungen bekommen wir als Wellenfunktion:

\( u(t,x) = A \sin (2\pi (\frac{c t}{\lambda} – \frac{x}{\lambda})) \\\)

Wobei A die Amplitude und λ die Wellenlänge sein soll.

Manchmal benutzt man auch die sog. Wellenzahl \( k = \frac{1}{\lambda} \).

Eine einfache Lösung der Wellengleichung im eindimensionalen Raum wäre (mit A=1, λ = 2π):

\( u(t,x) = \sin(x + ct) \)

Also eine eindimensionale Wellenfunktion.

Ebene Wellen

Eine ebene Welle ist eine Welle im dreidimensionalen Raum, deren Wellenfronten (d.h. Flächen gleichen Phasenwinkels) parallele Ebenen bilden. Die Ausbreitungsrichtung der Welle steht senkrecht dazu. Diese Richtung ist also räumlich konstant.

Siehe auch: Kugelwelle

Transversal – Longitudinal – Polarisierung

Eine Transversalwelle (Quer-, Schub- oder Scherwelle) ist eine Welle, bei der die Schwingung senkrecht zu ihrer Ausbreitungsrichtung erfolgt. Das Gegenteil ist eine Longitudinalwelle (Längswelle), bei der die Schwingung in Richtung der Ausbreitungsrichtung stattfindet.

Transversalwellen sind polarisierbar, da die Schwingung in der gesamten Ebene möglich ist, die senkrecht auf ihrer Ausbreitungsrichtung steht.

Stehende Wellen

Ein wichtiger Spezialfall sind sog. “Stehende Wellen”. Sie haben Knoten und Bäuche.

An einem festen Ende ist immer ein Knoten (Auslenkung Null) und an einem offenen Ende ist immer das Maximum eines Bauches.

Betrachten wir zwei feste Enden, so ist für die Gundschwingung: \( \frac{\lambda}{2} = L  \) und die Oberschwingungen ungerade Vielfache von lambda/2.

Weiterführendes

Stehende Wellen spielen eine Rolle

Physik: Thermodynamik – Wärmelehre

dkracht

Gehört zu: Physik
Siehe auch: Quantenmechanik, Physikalische Größen, Ideale Gase
Benutzt: WordPress-Plugin Latex

Stand: 29.06.2023   (neu: Zustandsgrößen)

Die Thermodynamik

Die Thermodynamik oder Wärmelehre ist eine natur- und ingenieurwissenschaftliche Disziplin. Das hauptsächliche Thema ist das Studium der Dampfmaschinen und die Frage, wie man Wärme in mechanische Arbeit umwandeln kann.

In der Thermodynamik (=Wärmelehre) werden wir erstmals irreversible Prozesse sehen. So etwas gab es in der klassischen Mechanik nicht.

Es gibt zwei Ansätze in der Thermodynamik: die statistische Sicht und die phänomenologische Sicht.  Statistisch werden ganz viele “Mikrozustände” betrachtet – Phänomenologisch geht es um die nach außen sichtbaren “Makrozustände”. Generell geht man davon aus, das sich die Mikrozustände in gewisser Weise vollkommen ungeordnet, eben stochastisch, verhalten.

Die physikalische Größe “Temperatur” wird in der Thermodynamik neu in die Physik eingeführt und ist eben eine “makroskopische” Größe.
Ausserdem wird eine weitere physikalische Größe, die “Entropie” eingeführt, die sehr schwer zu verstehen ist (dazu weiter unter: Zweiter Hauptsatz der Thermodynamik).

Phänomenologisch beschreiben wir den Zustand eines Systems oft durch die physikalischen Größen  Volumen, Druck und Temperatur (sog. Zustandsgrößen). Ein und der gleiche so beschriebene phänomenologischer Zustand kann dann aber durch viele unterschiedliche “mikroskopische” Zustände zustande kommen – eben statistisch.

Zustandsgrößen

Eine Zustandsgröße ist eine physikalische Größe, die – ggf. zusammen mit anderen – den Zustand eines physikalischen Systems zu einem gegebenen Zeitpunkt beschreibt und zwar unabhängig davon, auf welchem Wege er zustande gekommen ist; also unabhängig von der “Vorgeschichte” des Systems.

So sind beispielsweise Druck und Temperatur klassische Zustandsgrößen, aber die physikalische Größe “Arbeit” nicht. Letztere bezeichnet man dann als  sog. “Prozessgröße”.

Links:

Stichworte:

  • Wärme, Temperatur, Entropie
  • Ideales Gas
  • Irreversible Prozesse
  • Perpetuum mobile
  • Dampfmaschine
  • Thermodynamisches Gleichgewicht
  • Freiheitsgrade
  • Phasenraum

Temperatur – Thermodynamisches Gleichgewicht

Bringt man zwei Körper unterschiedlicher Temperatur zueinander in Kontakt, so stellt sich nach einer gewissen Zeit ein sog. “thermodynamisches Gleichgewicht” ein. Dann sind die Temperaturen beider Körper gleich.

So können wir schon einmal sagen, wann zwei Temperaturen gleich sind, aber haben noch keine Messskalen.

Temperatur – Messung der Temperatur

Die Temperatur ist eine Basis-Einheit des SI-Systems. Historisch wurde die Temperaturskala durch bestimme Fixpunkte festgelegt zwischen denen man dann interpolieren musste.

Als solche Fixpunkte hatte man benutzt Schmelzpunkte bzw. Gefrierpunkte von Wasser, Wasserstoff, Gold etc. Später ging man auch dazu über sog. Trippelpunkte als Fixpunkte zu benutzen.

Zur Interpolation zwischen solchen Fixpunkten nutzt man temperaturabhängege Eigenschaften von Körpern; wie z.B. die Längenausdehnung eines Metallstabes oder die Volumenausdehnung von Flüssigkeiten.

1948 wurde durch die 9. Generalkonferenz für Maß und Gewicht (CGPM) festgelegt, dass eine absolute thermodynamische Skala den Tripelpunkt des Wassers als einzigen fundamentalen Fixpunkt haben sollte. Vor allem die starke Abhängigkeit des Siedepunkts vom Luftdruck hatte die Temperatureichung über die bisherigen Fixpunkte schwierig gemacht. Der Tripelpunkt hingegen war leicht und eindeutig reproduzierbar.

1954 wurde das Kelvin von der CGPM in der bis zum 19. Mai 2019 gültigen Form definiert und zur Basiseinheit erklärt. Dadurch bekam zugleich das Grad Celsius eine neue Definition. Die Bezeichnung war zunächst „Grad Kelvin (°K)“ und wurde 1967 auf „Kelvin (K)“ geändert. Die Definition lautete seitdem: „Das Kelvin, die Einheit der thermodynamischen Temperatur, ist der 273,16-te Teil der thermodynamischen Temperatur des Tripelpunktes des Wassers.“.

2019: Anbindung an die thermische Energie: Die thermodynamische Temperatur ist direkt proportional zur thermischen Energie, mit der Boltzmann-Konstanten als Proportionalitätsfaktor  (1.380649 * 10–23 Joule/Kelvin). Solange die Einheiten von Energie (Joule) und Temperatur (Kelvin) unabhängig voneinander definiert waren, musste die Boltzmann-Konstante experimentell bestimmt werden. Diese Messungen wurden im Laufe der Zeit immer präziser und erreichten schließlich die Genauigkeit der Realisierung des Kelvin über den Tripelpunkt des Wassers. Damit war die Existenz zweier konkurrierender Definitionen nicht mehr zu rechtfertigen. Der Boltzmann-Konstanten wurde ein fester Wert in der Einheit J/K zugewiesen und das Kelvin dadurch direkt an das Joule gekoppelt. Der Wert der Boltzmann-Konstanten, die seitdem ein nur durch Konvention festgelegter Skalierungsfaktor ist, wurde so gewählt, dass das neue Kelvin möglichst genau mit dem alten übereinstimmte. Diese Änderung trat mit der Revision des Internationalen Einheitensystems am 20. Mai 2019 in Kraft.

Erster Hauptsatz der Thermodynamik

Der 1. Hauptsatz der Thermodynamik ist eine besondere Form des Energieerhaltungssatzes aus der Mechanik. In Worten bedeutet dies: Die Änderung der inneren Energie eines geschlossenen Systems ist gleich der Summe der Änderung der Wärmemenge und der Änderung der Arbeit.

In Formeln kann man das so ausdrücken:

\( \Delta U = \Delta Q + \Delta W \)

wobei:

  • U innere Energie des Systems
  • Q der Wärmeinhalt (Wärmemenge) des Systems – positiv, wenn dem System zugeführt – negativ, wenn aus dem System abgeführt
  • W die vom System geleistete mechanische Arbeit – positiv, wenn dem System zugeführt – negativ, wenn nach außen geleistet

Zweiter Haupsatz der Thermodynamik

Vorzugsrichtung von Prozessen. Der zweite Hauptsatz der Thermodynamik in der Formulierung von Rudolph Clausius (1822-1888) lautet: „Es gibt keine Zustandsänderung, deren einziges Ergebnis die Übertragung von Wärme von einem Körper niederer auf einen Körper höherer Temperatur ist.

Zustandsveränderungen können reversibel (wie in der klassischen Mechanik) oder irreversibel sein. Irreversible Prozesse laufen nur in einer Richtung ab und nicht umgekehrt. Bei reversiblen Prozessen bleibt die Entropie gleich, bei irreversiblen Prozessen nimmt die Entropie zu.

Der Zweite Hauptsatz der Thermodynamik kann mit Hilfe des Begriffs der Entropie auch so formuliert werden, dass die Entropie (eines geschlossenen Systems) niemals abnehmen kann.

Damit bekommt die Zeit eine Richtung.

Ideale Gase

Das Einfachste, mit dem sich die Thermodynamik gern befasst, sind die sog. Idealen Gase.

Boltzmann

Der österreichische Physiker Ludwig Boltzmann (1844-1906) beschreibt mit seiner “Boltzmann-Gleichung” die Dynamik eines idealen Gases und definiert die physikalische Größe Entropie über Mikro- und Makro-Zustände…

Thermodynamische Zustandsänderungen

Ein thermodynamischer Prozess kann zu einer thermodynamischen Zustandsänderung führen. Solche Zustandsänderungen (Prozesse) können reversibel oder irreversibel sein.

Zustandsgrößen beschreiben den Zustand eines thermodynamischen Systems; wobei es egal ist, auf welchem Wege man den betreffenden Zustand erreicht.

Typische Zustandsgrößen sind:

  • Volumen: V
  • Druck: p
  • Innere Energie: U
  • Entropie: S

Zustandsänderungen eines thermodynamischen Systems werden durch die Veränderung von Zustandsgrößen beschrieben.

  • Isotherme Zustandsänderung: Keine Temperaturänderung, also T=const. bzw. Δ U = 0
  • Adiabatische Zustandsänderung: Kein Wärmeaustausch, also Δ Q = 0

Veranschaulichen kann man sich solche Zustandsänderungen gut an einem p-V-Diagramm.

Klassische Definition der Entropie

Schon früher haben wir physikalische Größen kennengelernt, die “unabhängig vom Weg”  waren: In einem konservativen Kraftfeld war die Arbeit, die nötig ist, um von A nach B zu kommen weg-unabhängig. Deshalb konnen wir da die potentielle Energie und das Potential einführen.

Analoges macht in der Thermodynamik Rudolf Clausius (1822-1888) mit seiner klassischen Definition der Entropie (Formelzeichen: S). Die Entropie stellt so etwas wie ein Maß für die “Irreversibilität” dar. Die SI-Maßeinheit der Entropie ist Joule/Kelvin.

Zunächst betrachten wir nur Zustandsveränderungen – also Deltas. Damit definieren wir Entropieveränderungen als:

\( \Large \Delta S = \frac{\Delta Q}{T} \)

Der bekannte Carnot’schen Kreisprozess beschreibt im p-V-Diagramm ja eine geschlossene Kurve und ist insgesamt auch reversibel, da er ja aus vier Prozessschritten besteht, wovon jeder einzelne reversibel ist. Unsere Berechnungen des Carnot’schen Kreisprozesses hatten ja für die zwei isothermen Prozessschritte (w=warm, k=kalt) ergeben:

\( \Large\frac{\Delta Q_w}{T_w} + \frac{\Delta Q_k}{T_k} = 0  \)

Was uns zu einer generellen Formel (ohne Beweis) führt:

\( \Large \oint_\alpha \frac{d Q}{T} = 0 \)

für reversible Prozesse, die im p-V-Diagramm eine geschlossene Kurve “α” bilden.

In Analogie zum Potentialbegriff in einem Kraftfeld können wir auch hier ein “Potential” definieren, das wir “Entropie S(A)” am Aufsetzpunkt “A” nennen:

\( \Large S(A) = \int_O^A \frac{d Q}{T} \)

Mit einem festzusetzenden Referenzpunkt “O” .
Die physikalische Größe Entropie kann man in diesem Sinne sehr abstrakt definieren. Der Vorteil ist, dass die Entropie nun tatsächlich eine Zustandsgröße ist.

Statistische Definition der Entropie

Ludwig Boltzmann wird 50 Jahre nach Clausius eine schöne statistische Definition der physikalischen Größe Entropie geben.

Ein thermodynamischer Makrozustand (z.B. Druck eines Gases) kann durch sehr viele Mikrozustände der Gas-Moleküle (also Orte und Impulse) realisiert werden. Da wir es mit gigantisch großen Anzahlen von Molekülen zu tun haben setzen wir die Statistik ein und kommen zu Aussagen über Wahrscheinlichkeiten von Anordnungen (oder Unordnungen).

Die klassische Definition der Größe Entropie ist:

\( \Large S = k_B \log{P} \)

Wobei kB die Boltzmann-Konstante ist und P die Wahrscheinlichkeit mit der ein Makrozustand durch Mikrozustände eigenommen wird.

Durch die Benutzung des Logarithmus’ wird die Entropie zu einer richtigen extensiven (d.h. mengenartigen) physikalischen Größe. Wir können Entropie-Mengen sinnvoll addieren.

Die Frage ist dann noch, wo wir den Nullpunkt der Entropie setzen. Dazu hat Max Planck vorgeschlagen dass der Nullpunkt da liegen soll, wo es nur noch einen einzigen Mikrozustand gibt, durch den der Makrozustand realisiert werden kann. Das wäre ein ideales Kristallgitter in absoluter Ruhe. Also bei T=0 soll auch S=0 sein. Statt der Wahscheinlichkeit P benutzen wir dann also die Anzahl Mikrozustände Ω, die den Makrozustand realisieren. Max Planck war es auch, der vorgeschlagen hatte, die in der Formel vorkommende Konstante “Boltzmann-Konstante” zu nennen.

Damit kommen wir zu der berühmten Folmel, die auch auf Boltzmanns Grabstein auf dem Wiener Zentralfriehof steht:

\(\Large S = k_B \ln{\Omega} \)

 

 

 

Physik: Gravitation

dkracht

Gehört zu: Himmelsmechanik
Siehe auch: Die Keplerschen Gesetze, Schwarzes Loch, Newton, Langrange-Punkte, Ebbe und Flut, Kraftfeld und Potential
Benutzt: WordPress-Plugin MathJax-Latex

Stand: 25.2.2022

Kraftfelder und Potential

Kraftfelder, wie das der Gravitation, können wir durch das zugehörige Potential-Feld beschreiben.

In einem sog. “konservativen” Kraftfeld \( \vec{F}(r) \) können wir eine Potentielle Energie (bzw. ein Potential) definieren.  Der Begriff konservativ bedeutet dabei, dass der Energieerhaltungssatz gilt. Die entlang eines Weges im Kaftfeld geleistete Arbeit ist unabhängig von Weg und nur vom Anfangs- und Endpunkt des Weges abhängig. So kann eine skalares Feld, das Potential, definiert werden.

Ist das betrachtete Kraftfeld das Gravitationsfeld einer ruhenden Masse M, so ist das “Gravitationspotential” einfach:

\(  \Large V(r) = \space – G  \frac{M}{r}  \\ \)

Ist das betrachtete Kraftfeld das Elektrische Feld einer ruhenden elektrischen Ladung Q, so ist das “Coulomb-Potential” einfach:

\(  \Large V(r) = \space – \frac{1}{4\pi\epsilon_0}\frac{Q}{r}  \\ \)

Und umgekehrt ist das Kraftfeld \( \vec{F}(r) \) einfach der Gradient des Potentials. Also:

\( \vec{F}(r) = \enspace – k \enspace \nabla V(r) \)   (wobei k die Ladung bzw. Masse ist)

Das Gravitationsgesetz

Die Gravitation ist eine der vier Gundkräfte (Wechselwirkungen) im Standardmodell der Teilchenphysik.

Im Jahre 1668, formulierte Isaac Newton (1642-1727) das berühmte Gravitationsgesetz:

\( \Large F = G \frac{m \cdot M}{r^2}  \)

aus dem sich die Keplerschen Gesetze herleiten lassen…

Das Besondere der Erkenntnis von Newton ist nicht nur die Formulierung als eine einzige Formel, sondern auch, dass die Gravitationskraft zwischen allen Körpern im Universum wirkt. Beispielsweise kreisen die Jupitermonde gemäß diesem Gesetz um den Jupiter und ebenfalls kreisen Doppelsterne etc. aufgrund der Gravitation umeinander…

Zu den Zeiten Newtons beschäftigte sich die Physik in der Hauptsache und fast ausschließlich mit Mechanik. Newton (und Leibnitz) entwickelten die Infenitesimalrechung (engl. Calculus) mit der die Bewegung mechanischer Systeme durch die Wirkung von Kräften berechenbar gemacht werden konnte. Siehe dazu mein separater Artikel Newtonsche Mechanik.

Isaac Newton hat auch sehr viel über das Licht geforscht. Stichworte dazu wären: Teilreflektion, Newtonsche Ringe,…

Die Größe der Gravitationskonstante G wurde erst viel später durch das berühmte Experiment “Gravitationswaage” von Henry Cavendish (1731-1810) bestimmt.

In der Wikipedia finden wir:

\( \Large G = (6{,}674\,30\pm 0{,}000\,15)\cdot 10^{-11}\,\mathrm {\frac {m^{3}}{kg\cdot s^{2}}} \)

Eine ähnliche Formel wie hier für die Gravitationskraft zwischen zwei Massen haben wir in der Elektrostatik für die Elektrische Kraft zwischen zwei elektrischen Ladungen: Das Coulomb-Gesetz.

Die Gezeitenkraft

Ein ausgedehner Körper wird in einem Gravitationsfeld auseinander gezogen, weil die Gravitationskraft ja mit der Entfernung abnimmt. Die “Vorderseite” eines Körpers wird stärker angezogen als die “Hinterseite”. Je größer die Abmessung des Körpers in Richtung Vorderseite/Hinterseite ist, desto größer die auseinanderziehende “Gezeitenkraft” als Differenz der Kräfte vorne/hinten..

Die Erdanziehung

Wie wir alle aus der Schule wissen, haben wir auf der Erdoberfläche eine Gravitationsbeschleunigung von ca. 9,81 m/s2

Das Gravitationsgesetz (s.o.) können wir auch schreiben als:

\( \Large a = G \frac{M}{r^2}  \)

Wenn wir Kraft = Masse mal Beschleuigung, also F = m * a, benutzen.

Wenn wir den mittleren Erdradius als 6371 km annehmen, sind wir auf der Erdoberfläche also im Mittel 6371 km vom Erdmittelpunkt entfernt.
Die Erdmasse beträgt laut Wikipedia ca. 5,9772 * 1024 kg

Bei bekanntem Erdradius, bekannter Erdmasse und bekannter Gravitationskonstante kann man sich die mittlere Gravitationsbeschleunigung an der Erdoberfläche also ausrechnen:

\( \Large a = G \frac{5,9772 \cdot 10^{24}}{6371000^2} = 9,82  \)

Oder andersherum: Wenn man die Gravitationsbeschleunigung gemessen hat, den Erdradius kennt und die Gravitationskonstante misst (wie Henry Cavendish s.o.), kann man die Erdmasse bestimmen…

Die Kreisbahn (Kreisbewegung)

Für eine Kreisbahn mit dem Radius R wäre eine Zentripedalkraft erforderlich von:

\( F_Z = m \cdot \frac{v^2}{R}\)

So eine Zentripedalkraft soll durch die Gravitation des Zentralkörpers der Masse M bewirkt werden. Diese Gravitationskraft ist:

\( F_G = G \cdot \frac{m \cdot M}{R^2}\)

Rechnerisch ergibt sich daraus als Kreisbahngeschwindigkeit (sog. Erste kosmische Geschwindigkeit):

\( v_1 = \sqrt{\frac{G \cdot M}{R}}  \)

Was bei der Erde bedeuten würde: 7,91 km/s.
Das wäre eine (theoretische) Keisbahn mit dem Radius R; also einer Höhe von  Null Metern über der Erdoberfläche. Nehmen wir mal ein realistisches Beispiel: die ISS. Diese fliegt in ungefähr 400 km Höhe. Da kämen wir auf eine Geschwindigkeit von

\(\Large v = \sqrt{\frac{6.6743 \cdot 10^{-11} \cdot 5.9772 \cdot 10^{24}}{6371000 + 400000}} = 7.94 \enspace km/s \\ \)

Weiter draussen z.B. beim Mond ist die Kreisbahngeschwindigkeit kleiner. Da liegt die Kreisbahngeschwindigkeit nämlich so um 1 km/s.

Die Fluchtgeschwindigkeit

Damit ein Körper der Masse m von der Erdoberfläche entweichen kann, benötigt er eine kinetische Energie, die mindestens so groß ist wie seine potentielle Energie:

\( E_{kin} = \frac{m}{2} \cdot v^2 \)

Das Gravitationspotential auf der Erdoberfläche ist:

\( E_{pot} = \int\limits_{-\infty}^{R} G \cdot \frac{m \cdot M}{r^2} dr = G \cdot m \cdot M \cdot \left[ -\frac{1}{r} \right]_{-\infty}^R  =  -G \cdot m \cdot M \cdot \frac{1}{R}\)

Rechnerisch ergibt sich die Fluchtgeschwindigkeit (sog. Zweite kosmische Geschwindigkeit) zu:

\( v_2 = \sqrt{\frac{2 \cdot G \cdot M}{R}}  \)

Was bei der Erde bedeuten würde: 11,2 km/s

Diese Zahl beruht ausschließlich auf der Gravitation der Erde; soll heissen andere Einflüsse wie Erdrotation oder etwaige Swing-By-Manöver könnten diese erforderliche Geschwindigkeit reduzieren – wie etwa bei den Mondflügen oder Voyager Raumsonden…

Siehe auch: https://de.wikipedia.org/wiki/Fluchtgeschwindigkeit_(Raumfahrt)

Ein Schwarzes Loch

Bei einem Schwarzen Loch wäre die Fluchtgeschwindigkeit die Lichtgeschwindigkeit c.  Wenn wir v2 = c setzen ergibt sich:

\( c = \sqrt{\frac{2 \cdot G \cdot M}{R}}  \)

Aufgelöst nach dem Radius R ergibt sich:

\( R = \frac{2 \cdot G \cdot M}{c^2} \)

Bei einem solchen Radius könnte also kein Licht entkommen; deshalb werden solche Objekte “Schwarze Löcher” genannt. Bei einem kleineren Radius wäre die Fluchtgeschwindigkeit größer als die Lichtgeschwindigkeit; bei einem größeren Radius wäre die Fluchtgeschwindigkeit kleiner als die Lichtgeschwindigkeit. Man nennt diesen Radius den “Schwarzschild-Radius” oder auch den Ereignishorizont.

Genaugenommen müsste man hier die Gleichungen der Allgemeinen Relativitätstheorie (ART) verwenden, da wir hier mit Sicherheit relativistische Effekte wegen der starken Raumkrümmung hätten. Interessanterweise ist die Formel für den Ereignishorizont (Schwarzschild-Radius) aber bei der ART die gleiche wie hier in der “Milchmädchenrechnung”.

 

Mathematik: Komplexe Zahlen

dkracht

Gehört zu: Mathematik
Siehe auch: Quantenmechanik, Von Pytharoras bis Einstein, Schrödinger-Gleichung
Benutzt: WordPress-Plugin Latex

Stand: 29.7.2022

Die komplexen Zahlen

Ausgangspunkt ist die berühmte imaginäre Einheit: i2 = -1

Eine komplexe Zahl schreibt man gerne als Realteil und Imaginärteil:

z = x + i*y      x = Re(z)   und   y = Im(z)

Wobei x und y reelle Zahlen sind.

Mit den Komplexen Zahlen kann man auch die vier Grundrechnungsarten, so wie wir sie von den “normalen” d.h. reellen Zahlen her kennen, ausführen – Die komplexen Zahlen bilden, mathematisch gesagt, einen “Körper”.

Zu jeder Komplexen Zahl gibt es die “komplex konjugierte“, die mit gern mit einem Sternchen als Superskript schreibt:

zur komplexen Zahl: z = x + i*y
ist die konjugierte:   z* = x – i*y

Manchmal schreibt man die komplex konjugierte auch mit einem Strich über der Zahl. Also:

\( \overline{x + y \cdot i} = x – y \cdot i \)

 

Jede Komplexe Zahl hat auch einen “Betrag” (kann man sich als Länge vorstellen):

|z|2 = x2 + y2

Interessanterweise ist der Betrag (Länge) einer Komplexen Zahl auch:

|z|2 = z z*

Darstellung der komplexen Zahlen mit kartesischen Koordinaten

Die Reellen Zahlen konnte ich mir ja durch die sog. Zahlengerade gut veranschaulichen. Die Komplexen Zahlen würde ich mir dann durch die Punkte in einer Ebene veranschaulichen.

Polar-Darstellung der komplexen Zahlen

Wenn komplex Zahlen einfach als Punkte in der Ebene verstanden werden können, kann ich sie anstelle von kartesischen Koordinaten, alternativ auch in durch sog. Polarkoordinaten darstellen; d.h. durch die Entfernung vom Nullpunkt r und den Winkel mit der reellen Achse φ.

Für eine Komplexe Zahl z = x + i*y  gilt:

r² = x² + y²

tan φ = x/y

\(\displaystyle \tan{ \phi} = \frac{x}{y} \)

Exponential-Darstellung der komplexen Zahlen

Die Eulerschen Formel ist:

\(\Large  e^{i  \cdot \phi} = \cos \phi+i \cdot \sin \phi \\\)

Damit können wir jede komplexe Zahl auch in sog. Exponential-Darstellung schreiben:

\(\Large z ={r} \cdot e^{i  \cdot \phi} \\ \)

Das funktioniert so gut, weil die Multiplikation von Potenzen der Addition der Exponenten entspricht und das mit den Summenformeln der Trigonometrie übereinstimmt.

Den Winkel φ nennt man auch “die Phase”.

Wenn die Komplexen Zahlen den Betrag 1 haben, also auf dem Einheitskreis liegen, hat man:

\( e^{i \phi} = cos{\phi} + i sin{\phi} \)

und man spricht von einer “reinen Phase”.

In der Quantenmechanik wird diese Exponentialdarstellung gerne benutzt, u.a. weil man damit die Multiplikation komplexer Zahlen sehr anschaulich darstellen kann:

\(\Large z_1 \cdot z_2 = {r_1 \cdot r_2} \cdot e^{i  \cdot (\phi_1 + \phi_2)} \\ \)

Sie auch Youtube-Video:

Die Eulersche Zahl

Definition der Eulerschen Zahl

Die Zahl e wurde von Leonhard Euler (1707-1783) als Grenzwert der folgenden unendlichen Reihe definiert:

\(\displaystyle e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} +  \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} + …   \)

Oder:

\(\displaystyle e = \sum_{n=0}^{\infty} \frac{1}{n!} \)

Die Exponentialfunktion

Potenzen zur Basis e bilden die Exponentialfunktion, auch e-Funktion genannt:

f(x) = ex

Die Ableitung (Differentialquotient) der e-Funktion ist wiederum die e-Funktion:

f'(x) = ex

Damit ergibt sich als Taylorsche Reihenentwicklung um den Entwicklungspunkt x0 = 0

\(\displaystyle f(x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}  + …  + \frac{x^n}{n!} + …   \)

Allgemein wäre die Taylor-Reihe ja:

\( \displaystyle T_\infty(x;x_0) = \sum_{k=0}^{\infty} \frac{f^(k)(x_0)}{k!} (x-x_0)^k \)

Da der Funktionswert und alle Ableitungen der e-Funktion an der Stelle x0 = 0 sämtlich 1 sind, vereinfacht sich die Darstellung wie oben gezeigt.

Physik: Teilreflektion

dkracht

Gehört zu: Physik, Quantenmechanik

Teilreflektion

Die Teilreflektion von Licht an einer Oberfläche hat schon Isaac Newton, der ja von einer Teilchennatur des Lichtes ausging, beschäftigt. Dies ist eines der Paradebeispiele der Quantenmechanik, die ja Aufenthaltswahrscheinlichkeiten für Teilchen ausrechnen will.

Wenn ein monochromatischer Lichtstrahl auf eine Glasplatte scheint, haben wir das Phänomen der Teilreflektion.

Das Ereignis “Reflektion eines Photons an der Grenzschicht Luft/Glas”  habe die Wahrscheinlichkeit von 4% = 4/100 = 1/25. Die Wellenfunktion dieses Ereignisses wäre also ein Vektor der Länge Sqrt{1/25} = 1/5 = 0.2.

Die Drehung des Vektors wäre proportional der Zeit, die das Licht braucht um den Weg zurückzulegen. Wenn wir die Teilreflektion an der dünnen Glasschicht betrachten, spielt nur die Differenz der Laufzeiten eine Rolle, wenn wir die Differenz der Drehwinkel bestimmen wollen..

So bekommen wir gute Beispiele an denen sich Auswirkungen der Quantenphysik in alltälichen Phänomenen demonstieren lassen.

 

 

Physik: Kreisbahn – Zentrifugalkraft – Zentripedalkraft – Drehimpuls

dkracht

Drehimpuls gehört zu: Astronomie, Physik, Himmelsmechanik
Siehe auch Keplersche Gesetze, Sonnensystem, Gravitation, Bohrsches Atommodell
Benutzt: WordPress-Plugin Latex

Stand: 16.12.2024

Zentrifugalkraft in einer Kreisbahn

Wenn ein Körper der Masse m (z.B. Planet oder ein Elektron im Bohrschen Atommodell) eine Kreisbahn mit dem Radius r beschreibt, so muss aus Sicht des Körpers eine Kraft in Richtung vom Mittelpunkt der Kreisbahn weg wirken:

\( F = \frac{m \cdot v^2}{r} \)

Diese Kraft nennt man “Zentrifugalkraft“. Das Bezugssystem des auf einer Kreisbahn befindlichen Planeten ist kein Inertialsystem. Die Zentrifugalkraft ist eine “Trägheitskraft” (auch Scheinkraft genannt). Die Kreisbahn kommt dadurch zustande, dass eine Kraft gleicher Größe in entgegengesetzter Richtung (Zentripedalkraft genannt) wirkt.

Kreisbahnen im Sonnensystem

Im Sonnensystem wirkt die Anziehungskraft (Graviationskraft) des Zentralkörpers Sonne (Masse M) als Zentripedalkraft auf einen Planeten (Masse m)  man hat also:

\(\frac{m \cdot v^2}{r} = G \cdot \frac{m \cdot M}{r^2}\)

Für die Kreisbahngeschwindigkeit im Sonnensystem gilt also:

\( v = \sqrt{\frac{ G \cdot M} {r}} \)

Dies ist auch ein Ausgangspunkt der Forschungen von Vera Rubin (1928-2016), die die Rotationsgeschwindigkeit in Galaxien bei unterschiedlichen Abständen vom Zentrum untersucht hat und dadurch die Existenz von sog. Schwarzer Materie bekräftigtigen konnte.

Mit den Mitteln der Vektoralgebra ausgedrückt ergibt sich die Bahngeschwindigkeit bei einer Kreisbewegung zu:

\( \vec{v} = \vec{\omega} \times \vec{r} \\ \)

Die kinetische Energie eines Planeten auf einer Kreisbahn mit dem Radius R ist:

\( E_{kin}(R) = \Large\frac{m}{2} \cdot v^2 = \frac{m}{2} \cdot \frac{G \cdot M}{R}\\\)

Die potenzielle Energie ist:

\( E_{pot}(R) = \Large \int\limits_{-\infty}^R m G M r^{-2} dr = m G M \left[-\frac{1}{r}\right]_{-\infty}^R = -m\frac{GM}{R}\)

Wasserstoffatom

Im Wasserstoffatom wirkt die elektrostatische Kraft (Elektrisches Feld) des Atomkerns  (Ladung q1) auf ein Elektron (Ladung q2) als Zentripedalkraft; man hat also:

\(\Large \frac{m \cdot v^2}{r} =   \frac{1}{4 \pi \epsilon_0} \frac{q_1 \cdot q_2}{r^2}  \\\)

Für die Kreisbahngeschwindigkeit im Bohrschen Atommodell gilt also:

\( v^2 = \Large \frac{1}{4 \pi \epsilon_0 m} \frac{q_1 \cdot q_2}{r} \\ \)

Definition des Drehimpulses

Klaro: Bei einer Rotation eines Systems vom Trägkeitsmoment J mit einer Winkelgeschwindigkeit ω habe ich einen Drehimpuls:

\( L = \omega \cdot J \\ \)

Da erhebt sich die Frage, was eigentlich ein “Trägheitsmoment” sein soll…

Im einfachen Fall von Körpern der Masse m (z.B. ein Planet) auf einer Kreisbahn vom Radius r (z.B. Sonnensystem) folgt aus der allgemeinen Definition des Trägheitsmoments J:

\( J = m \cdot r^2 \\\)

Damit wäre der Drehimpuls:

\( L = \omega \cdot m \ r^2 \\\)

Wenn wir dies mit der Bahngeschwindigkei \( v = \frac{2 \pi \cdot r}{T}  \) ausdrücken wollen, benutzen wir die Beziehung:
\( \omega = \frac{v}{r} \) und erhalten:

\(L = v \cdot m \cdot r \\\)

Gemessen wird der Drehimpuls also in den SI-Einheiten: \( \Large \frac{m^2 kg}{s} \)

Drehimpuls und die Keplerschen Gestze

Wenn der Drehimpuls eine Erhaltungsgröße ist, folgt aus obiger Gleichung sofort das 2. Keplersche Gesetz.

Beispiele der Erhaltung des Drehimpulses

Wir alle kennen das Beispiel der Pirouette einer Eistänzerin. Wenn die Arme angezogen werden, verringert sich das Trägheitsmoment und die Winkelgeschwindigkeit steigt an, da der Drehimplus erhalten bleibt.

 

Physik: Relativitätstheorie, Raum-Zeit-Diagramme, Lorentz-Transformation, Minkowski-Metrik und Eigenzeit

dkracht

Gehört zu: Physik
Siehe auch: Kosmologie, Tensoren, Lineare Algebra, Metrik, Allgemeine Relativitätstheorie, Quantenfeldtheorie, Schwarzes Loch
Benutzt: WordPress-Plugin Latex, Grafiken von Github, Grafiken von Wikipedia

Stand: 08.12.2024  (Vierer-Vektor, Minkowski-Metrik ausführlicher, Weltlinie, Eigenzeit, Loedel, Lorentz-Faktor, Penrose)

Überschneidungen mit: Relativitätstheorie

Was ist mit “Relativität” gemeint?

Der Begriff der “Relativität” von physikalischen Vorgängen dreht sich darum, dass ein und dieselbe Beobachtung von verschiedenen Beobachtern in verschiedenen Koordinatensystemen gemacht wird. Bei den oben genannten “physikalischen Vorgängen” handelt es sich um die Messung physikalischer Größen wie:

  • Zeit
  • Ort
  • Geschwindigkeit
  • Impuls
  • Beschleunigung
  • Kinetischen Energie
  • Elektromagnetische Kaft
  • Maxwell-Gleichungen
  • …

Dabei könnten zwei Beobachter immer zu übereinstimmenden Ergebnissen kommen (so etwas nennt man dann “invariant”) oder es ergeben sich manchmal unterschiedliche Ergebnisse (“variant”). Im letzteren Fall kommt es also darauf an, welcher Beobachter diese Messung gemacht hat. Somit sind die Ergebnisse also “relativ” zu einem bestimmten Beobachter zu sehen.

Im Falle einer solchen Relativität möchte man die Messergebnisse zwischen Beobachtern formelmäßig “transformieren” können.
Dafür betrachten wir zunächstmal den einfachen Fall, dass sich die Beobachter, gleichförmig und gradlinig zu einander bewegen, also ohne Beschleunigung. Solche Beobachter bzw. deren Koordinatensysteme (Ort und Zeit) nennen wir “Inertialsysteme“.
Ein Beobachter beobachtet Ereignisse, denen er jeweils Ort und Zeit zuordnet.

Raum-Zeit-Diagramm

Solche Ereignisse kann man sich als Punkte in einem sog. Raum-Zeit-Diagramm veranschaulichen, wo die auf der einen Achse die drei Raum-Dimensionen x, y, z auf eine Dimension vereinfacht werden: x. Es bleibt als zweite Achse die Darstellung der Zeit, wobei es sich später als elegant erweisen wird, statt der “echten” Zeit das Produkt aus Lichtgeschwindigkeit und der Zeit, also c · t abzutragen.

Ein Minkowski-Diagramm ist eine ganz einfache grafische Darstellung, nämlich ein rechtwinkliges zweidimensionales Koordinatensystem mit einer Zeitachse und einer Raumachse (also der dreidimensionale Raum auf eine Dimension vereinfacht). Ein Punkt im Minkowski-Diagram wird auch Ereignis genannt, denn der Punkt beschreibt Ort und Zeit. Die Bewegung eines Punktes ist eine Linie im Raum-Zeit-Diagramm und wird seine Weltlinie genannt.

Punkte, die sich gleichförmig und gradlinig bewegen, haben dann als Weltlinie eine Gerade im Raum-Zeit-Diagramm.

Abbildung 1: Minkowski-Diagramm: Weltlinie eines Photons (Github: Minkowski_Diagram_Photon.svg)

Weltlinie eines Photons

Die Weltlinien von Teilchen mit konstanter Geschwindigkeit sind Geraden im Minkowski-Diagramm. Üblicherweise wählt man die Einheiten auf den Achsen so, dass die Weltlinien von Licht (Photonen) eine Steigung von 45 Grad haben.

Mit so einem Raum-Zeit-Diagramm stellen wir also einen 2-dimensionalen Vektorraum dar und suchen nach Transformationen, die Koordinaten eines Punktes (Ereigniss genannt) von einem Koordinatensystem in ein anderes transformieren. Da es sich bei den Koordinatensystemen um Intertialsystem handeln soll, könnten wir vermuten, dass die Transformationen auch ganz einfache sind z.B. Linerare Transformationen, die dann als Matrix dargestellt werden könnten.

Relativität bei Galileo

Bei Galileo (1564-1642) sind die die physikalischen Gesetze, speziell die Bewegungsgleichungen, identisch in allen Inertialsystemen. Es gibt kein bevorzugtes System, was etwa “in Ruhe” wäre. Jede Bewegung muss relativ zu einem Bezugspunkt gemessen werden.

Speziell für Geschwindigkeiten gilt nach Galileo das auch intuitiv einleuchtende “Additionsgesetz” d.h. wenn ein Beobachter in seinem System ein Objekt mit der Geschwindigkeit v1 misst, dann wird ein anderer Beobachter, der sich relativ zum ersten Beobachter mit der Geschwindigkeit v bewegt, die Geschwindigkeit desselben Objekts zu v2 = v1 + v messen. Wobei da noch die Richtungen berücksichtigt werden müssen, also: \( \vec{v_2} = \vec{v_1} + \vec{v} \)

Auch die Lichtgeschwindigkeit wäre in unterschiedlichen Inertialsystemen unterschiedlich.

Die Galilieo-Transformationsgleichungen wären demnach:

\(  \tilde{t} = t \\ \tilde{x} = -v \cdot t + x \\ \)

Was als Galileo-Transformationsmatrix ergibt:

\( F = \left[ \begin{array}{rr} 1 & 0 \\  -v & 1 \\  \end{array} \right] \\ B = \left[ \begin{array}{rr} 1 & 0 \\  v & 1 \\  \end{array} \right] \)

Wobei F (=foreward) und B (=backward) wieder die Identität ergeben.

Youtube Video eigenchris 103d: https://youtu.be/ndjiLM5L-1s

Abbildung 2: Galilio-Transformation (Github: Gallileo.svg)

Gallilieo.svg

Gallileo/Newton-Transformation (blau -> rot)

Bei der Koordinatentransformation nach Gallileo/Newton verschiebt sich “nur” die x-Achse, die Zeit (t) ist in jedem bewegten Inertialsystem gleich. Deswegen würde jede Geschwindigkeit (also auch die Lichtgeschwindigkeit) verändert.

Lorentz & Co.

Die sog. Lorentz-Transformationen entstanden nach 1892 um zunächst die damals vorherrschende Äthertheorie in Einklang mit den Ergebnissen des Michelson-Morley-Experiments zu bringen. (Albert A. Michelson 1881 in Potsdam). Die Lorentz-Transformationen wurden erst 1905 von Heny Poicaré (1854-1912)  so formuliert, wie wir sie heute kennen:

\(  c \cdot \tilde{t} = \gamma (ct – \beta x) \\ \tilde{x} = \gamma ( -\beta c t + x) \)

wobei \( \beta = \frac{v}{c}  \) und \( \gamma = \frac{1}{\sqrt{1-\beta^2}} \)

Wobei diese Faktoren so bestimmt sind, dass die Lichtgeschwindigkeit in allen Intertialsystemen gleich ist.

Als Lorentz-Transformationsmatrix ergibt sich:

\( F = \gamma \left[ \begin{array}{rr} 1 & -\beta \\  -\beta & 1 \\  \end{array} \right] \\ B = \gamma \left[ \begin{array}{rr} 1 & +\beta \\  +\beta & 1 \\  \end{array} \right] \)

Youtube Video eigenchris 104b: https://youtu.be/240YGZmV1b0

Abblidung 3: Lorentz-Transformation (Github: Lorentz.svg)

Lorentz Transformation

Lorentz-Transformation (blau -> rot)

Bei der Lorentz-Transformation werden beide Achsen in Richtung auf die Diagonale gedreht. Dadurch werden die ursprünglichen Quadrate zu Rhomben und die Lichtgeschwindigkeit beibt gleich (die Diagonale). Damit bleibt die Skalierung (also die Achsenteilungen) bei der Lozenz-Transformation so, dass die Flächen der Rhomben gleich den Flächen der ursprünglichen Quadrate sind. Für diese Skalierung sorgt der sog. Lorentz-Faktor γ (siehe oben).

Wenn man in so einem Minkowski-Diagramm zwei Intertialsysteme darstellen will, ist das eine rechtwinklig (chartesisch) und die Achsen des anderen sind gemäß Lorentz-Transformation schief dazu – das stört bei Manchen das ästetische Empfinden. Deshalb greift man in so einem Fall auch manchmal zu einer Variante des Minkowsiki-Diagramms, dem Loedel-Minkowsik-Diagramm (nach Ernesto Palumbo Loedel 1901-1962).

Auch der Begriff der Gleichzeitigkeit wird relativ (https://en.wikipedia.org/wiki/Relativity_of_simultaneity)

Abbildung 4: Gleichzeitigkeit (Wikipedia: https://en.wikipedia.org/wiki/Relativity_of_simultaneity#/media/File:Relativity_of_Simultaneity_Animation.gif)
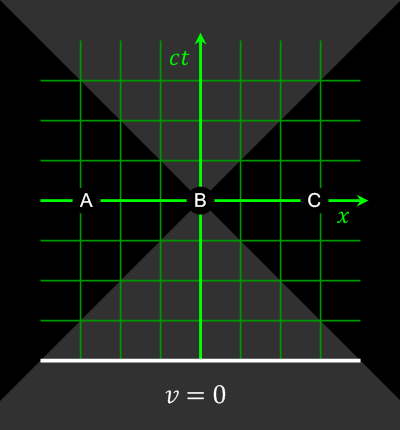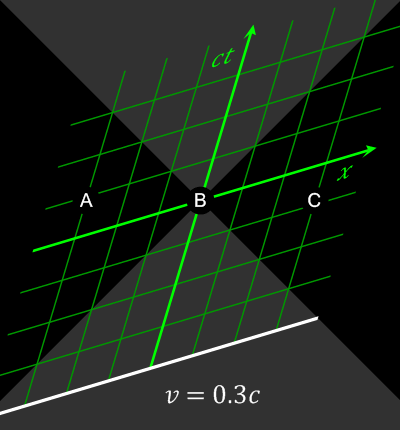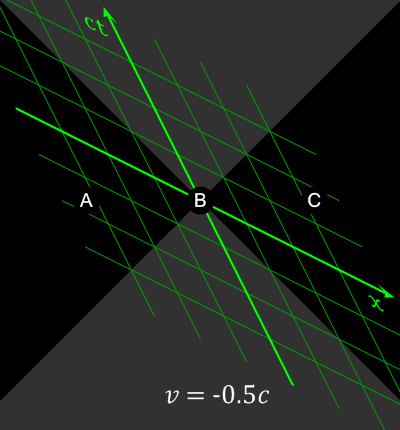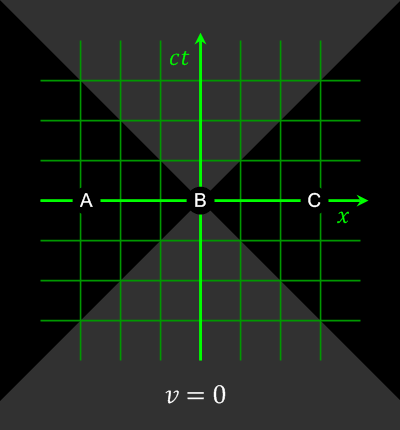
Relativity of Simultaneity (Copyright: Wikipedia)

Bei Ereignissen, die raumartig (s.u.) getrennt sind (|x| > ct) kann durch eine Lorentz-Transformation die Gleichzeitigkeit und damit die Kausalität relativiert werden.

SRT Einsteins Spezielle Relativitätstheorie

Dazu habe ich einen eigenen Blog-Artikel geschrieben: Spezielle Relativitätstheorie

SRT Minkowski-Raum – Minkowski-Metrik – Linienelement

Hermann Minkowski (1864-1909) war Mathematiker und lehrte an den Universitäten Bonn, Königsberg, Zürich und hatte schließlich einen Lehrstuhl in Göttingen. In Zürich war er einer der Lehrer von Albert Einstein.

Auf Minkowski geht die Idee zurück, die Welt (wie Lorenztranformation und Spezielle Relativitätstheorie) als einen nicht-euklidischen vierdimensionalen Raum zu verstehen. Wobei er mit  anschaulichen Bildern (grafischen Darstellungen) anstatt mit schwerer verständlichen Formeln arbeitete.

Zwei Begriffe kommen sofort bei “Minkowski” ins Gespräch:

  • Minkowski-Raum
  • Minkowski-Diagramm

Der Minkowski-Raum ist eine “größere Geschichte”: Ein vierdimensionaler Raum mit einer speziellen Metrik, denn in einem Raum möchte man ja Abstände zweier Punkte messen, Länge von Vektoren, Winkel und Flächen bestimmen.  Eine solche Metrik kann man beispielsweise durch ein Skalarprodukt von Vektoren definieren.
Eine einfache Definition der Metrik im Minkowski-Raum ist gegeben durch (“Linienelement”):

ds²  = c² dt² – (dx² + dy² + dz²)

Soetwas schreiben die Oberspezialisten gern als einen Tensor, auch “metrischer Tensor” genannt:  \( ds^2 = g_{\mu \nu} dx^{\mu} dx^{\nu}\) (bei einem Tensor wird “implizit” summiert.)

Wenn man unser Universum als Minkowski-Raum verstehen wollte, mit einer durch das Linienelement

ds²  = c² dt² – (dx² + dy² + dz²)

definierten Metrik, wäre das ein “flacher” Raum, also nicht gekrümmt (so zu sagen ohne Gravitation).

In so einem Minkowski-Raum, also mit der Minkowski-Metrik, lässt sich die Spezielle Relativitätstheorie (SRT) sehr einfach grafisch darstellen.

Das Linienelement der Minkowski-Metrik

Hermann Minkowski (1864-1909) war ein deutscher Mathematiker, der zeitweise auch Einsteins Lehrer in Zürich war.

Ein Minkowski-Diagramm ist ja relativ locker definiert (s.o.). Da haben wir eben die Zeit als weitere Dimension und beschreiben damit eine Ereignis in der Raumzeit durch einen Punkt mit vier Koordinaten:

Ereignis: e = (t, x, y, z)

Von einem Minkowski-Raum spricht man, wenn man auch noch eine Metrik hat, womit dann Abstände definiert werden. Allerdings wollen wir eine Metrik, die Lorentz-invariant ist; d.h. der Abstand zweier Ereingnisse (Punkte) soll in allen Inertialsystemen, die durch Lorentz-Transformation in einander übergehen, der gleiche sein. Mit einem einfach gedachten Linienelement:

ds²  = c² dt² + dx² + dy² + dz²

funktioniert das leider nicht (kann man ausrechnen).

Als sog. Minkowski-Metrik definiert man stattdessen das Linienelement:

ds²  = c² dt² – (dx² + dy² + dz²)

Die dadurch definierte Metrik ist tatsächlich Lorentz-invariant (kann man ausrechnen). Formal wird diese Minkowski-Metrik definiert durch einen Metrik-Tensor, den sog. Minkowski-Tensor (siehe dort).

So eine Metrik definiert zunächsteinmal die Länge eines Vektors \( \vec{S} = ( x^1, x^2, x^3, x^4 ) \) als:

\( || \vec{S} || = \sqrt{\vec{S} \cdot \vec{S}} = \sqrt{g_{ij} x^i x^j}  \)

Um den Abstand zweier Ereignisse in unserer Raumzeit  s1 = (t1, x1, y1, z1) und s2 = (t2, x2, y2, z2) zu ermitteln, nehmen wir die Länge des Differenz-Vektors:

\(  s^2 = || s_2 – s_1 || =  c^2 (t_2 – t_1)^2 – (x_2 – x_1)^2 – (y_2 – y_1)^2 – (z_2 – z_1)^2  \)

In so einem Minkowski-Raum, also mit der Minkowski-Metrik, lässt sich die Spezielle Relativitätstheorie (SRT) demnach sehr einfach grafisch darstellen eben weil diese Metrik Lorentz-invariant ist.

Man sagt auch: Wenn man unser Universum als Minkowski-Raum verstehen wollte, mit dieser Metrik,  wäre das ein “flacher” Raum, also nicht gekrümmt (so zu sagen ohne Gravitation).

Raumartig, Zeitartig, Lichtartig

Für den Abstand zweier Ereignisse können wir unterscheiden:

  • \( s^2 > 0 \) : Der Abstand wird “zeitartig” genannt – die Ereignisse sind zeitartig getrennt
  • \( s^2 < 0 \) : Der Abstand wird “raumartig” genannt – die Ereignisse sind raumartig getrennt
  • \( s^2 = 0 \) : Der Abstand wird “lichtartig” genannt

Auf eine Raum-Dimension vereinfacht, ist der Minkowski-Abstand: \( s^2 = c^2 t^2 – x^2 \). Damit ist dann:

  • Zeitartiger Abstand: \( x < ct \)
  • Raumartiger Abstand:   \( x > ct \)
  • Lichtartiger Abstand: \( x = ct \)

Abblidung 5: Minkowski-Metrik (Github: Minkowski-02.svg)

Minkowski-02.svg

Kurven als Weltlinie

Die Begriffe “raumartig” (space like) und “zeitartig” (time like) werden auch für Kurven im Minkowski-Diagramm verwendet.
Dabei betrachtet man infenitesimal kleine Kurvenstücke und fragt sich, ob diese als Intervall immer raumartig oder immer zeitartig sind.
Ein wichtiges Thema sind “closed timelike curves”…

Minkowski-Abstand

Man darf sich von der Optik des Minkowski-Diagramms nicht zu vereinfachten Schlüssen verführen lassen. Bei einem Minkowski-Abstand von: \( s^2 = c^2 t^2 – x^2 \) liegen beispielsweise alle Punkte (Ereignisse), die vom Koordinatenursprung den Minkowski-Abstand 1 haben, nicht auf der Kugelschale mit Radius 1, sondern die Menge (ct, x):

\( 1 = {ct}^2 – x^2 \)

Das ist eine Hyperbel im Minkowski-Diagramm. Dort liegen also alle Punkte im ursprünglichen Bezugssystem (ct,x), die eine Abstand 1 vom Koordinatenursprung haben.

Da dieser Anstand invariant ist, liegt dort also auch für jedes Lorenz-transformierte Bezugssystem (ct’, x’) der Punkt auf der transformierten Raum-Achse, der einen Abstand 1 vom Ursprung hat.

Wir müssen also immer daran denken, dass im Minkowski-Raum nicht die vom Diagramm “vorgegaukelte” Euklidische Geometrie gilt, sondern der Minkowski-Abstand.

Abbildung 6: Minkowski-Abstand (Github: hyperbel.svg)

Hyperbel.svg

Minkowski-Metrik

Vierer-Vektoren

Im Raum-Zeit-Diagramm ist ein Punkt ein Ereignis, beschrieben durch seinen Ort im Raum und den Zeitpunkt; man benötigt im dreidimensionalen Raum also 4 Koordinaten (siehe Koordinatensysteme). Man spricht deswegen auch von einem Vierer-Vektor:

\( \vec{S} =  \left[ \begin{array}{c} c t \\\ x \\\ y \\\ z  \end{array} \right] \\\)

Mit der Vektor-Basis ausgedrückt ist das:
\( \vec{S} = ct \cdot \vec{e_t} +  x \cdot \vec{e_x}  + y \cdot \vec{e_y} + z \cdot \vec{e_z} \\ \)

Entsprechend hätte man Vierer-Geschwindigkeit, Vierer-Impuls, Vierer-Beschleuigung etc.

In der Physik interessiert oft die Veränderung einer Größe mit der Zeit. Dazu müsten wir nach er Zeit differenzieren.

Der springende Punkt bei diesen “Vierer-Vektoren” ist aber nicht die eigentlich triviale Tatsache, dass die Vektoren vier Komponenten haben, sondern die Art und Weise, wie nach der Zeit differenziert wird. Die Zeit-Koordinate (“Koordinatenzeit”) ist ja in jedem Interialsystem eine andere, weshalb für die Differenzierung von Vierer-Vektoren nach der Zeit die sog. Eigenzeit (engl. proper time, Symbol τ) genommen wird. Wobei beim Differenzieren von dieser Vektoren genaugenommen die covariante Ableitung genommen wird.

Bei einer genaueren Definition des Begriffs “Vierer-Vektor” würde man noch die Invarianz der Vektor-Länge bei Lorenztransformationen fordern. Die Länge eines Vierer-Vektors ergibt sich dabei durch die Metrik.

Solche Vierervektoren spielen eine wichtige Rolle bei den Einsteinschen Feldgleichungen der ART.

Siehe auch: http://walter.bislins.ch/blog/index.asp?page=Bewegungsgleichung+der+Speziellen+Relativit%E4tstheorie

Eigenzeit in der Minkowski-Metrik

Als Eigenzeit (Symbol τ) eines bewegten Objekts (entlang einer beliebigen Weltlinie) bezeichnet man die Zeit, die eine “mitbewegte” Uhr  zeigt. Jede Weltlinie hat eine eigene Eigenzeit.
Wir werden sehen: Die Eigenzeit ist die auf einer Weltlinie gemessene Länge in der Minkowski-Metrik und deshalb auch Lorenz-invariant.

Im Gegensatz dazu ist die Zeitkoordinate (auch Koordinatenzeit) eben eine von vier Koordinaten im verwendeten Koordinatensystem und transformiert sich, wenn wir auf ein anderes Koordinatensystem übergehen.

Für den einfachen Fall eines Objektes, dass sich geradlinig mit konstanter Geschwindigkeit \( \vec{v} \) bezüglich unseres Bezugssystems (ct, x) bewegt, ist das ganz einfach. Dann ist die Weltlinie dieses Objekts eine Gerade in unserem Koordinatensystem und wir häten die Bewegung:

\(  x(t) = ||\vec{v}|| \cdot t \)

Wir können an ein solches Objekt dann ein Koordinatensystem (ct’, x’) “anheften”, was wieder ein Intertialsystem wäre. Man spricht vom “mitbewegten” System. Den Zusammenhang liefert die Lorenz-Transformation. Wenn wir jetzt einen Zeitabschnitt von \(\Delta t \) (in unserem Bezugssystem) betrachten, wäre die Frage. welche Zeit im mitbewegten Bezugssystem dann vergeht.

\( \Delta t^{\prime} = \sqrt{1-\frac{||v||^2}{c^2}} \cdot \Delta t \)

Wenn wir nun ein Objekt betrachten, dass sich nicht auf einer Geraden als Weltlinie bewegt, wäre ein mitbewegtes Bezugssystem kein Inertialsystem mehr. Die dort vergangene Zeitspanne von ta bis te, also die Eigenzeit, ergibt sich dann aufintegriert als:

\(  \tau =  \displaystyle\int\limits_{t_a}^{t_e} \sqrt{1-\frac{||v(t)||^2}{c^2}} \, dt \)

Diese Eigenzeit τ würde dann von allen Intertialsystemen aus gesehen gleich sein d.h. Lorenz-invariant.

Euklidische Vektoren

Im klassischen Eukidischen Raum (soll heissen ohne die SRT) haben wir es generell mit 3er-Vektoren zu tun:

Ortsvektor: \( \vec{r} = x \cdot  \vec{e_x} + y \cdot \vec{e_y} + z \cdot \vec{e_z} \)

Geschwindigkeit: \( \vec{u} = \frac{d \vec{r}}{d t} \)

Impuls: \( \vec{p} = m \cdot \vec{u} \)

Beschleunigung: \( \vec{a} = \frac{d^2 \vec{r}}{d t^2} = \frac{d \vec{u}}{d t} \)

Kraft: \( \vec{f} = \frac{d \vec{p}}{d t} = m \cdot \vec{a} \)

Minkowski-Vektoren

Wenn wir das Obige nun nach SRT und in beliebigen Inertialsystemen betrachten wollen, haben wir gleich ein Problem mit den Ableitungen nach der Zeit. In jedem Inertialsystem verläuft die Zeit (auch Koordinatenzeit genannt)  anders; d.h. die o.g. Größen sind nicht mehr Lorenz-invariant.

Lorenz-invariant sind zunächst:

  1. Die Lichtgeschwindigkeit: c
  2. Der Minkowski-Abstand zweier Ereignisse: \( S = c \cdot (t_2 – t_1) – (x_2 – x_1)^2 – (y_2 – y_1)^2 – (z_2 -z_1)^2   \)

Einerseits ist die Zeit eine Koordinate in der vierdimensionalen Raumzeit, andererseits können wir zeitliche Abstände zwischen zwei Ereignissen messen.

Anstelle der Zeit (Koordinatenzeit), die in allen Inertialsystem verschieden sein kann, definieren wir eine sog. Eigenzeit τ, die invariant sein soll. Danach können die das differenzieren und kämen zu invarianten Größen….

Bei den Minkowski-Vektióren (Vierervektoren) gehen wir aus vom Ortsvektor, der die Bewegung eines Massepunkts m in seiner Eigenzeit beschreibt (Weltlinie):

\( \vec{S} = ct \cdot \vec{e_t} +  x \cdot \vec{e_x}  + y \cdot \vec{e_y} + z \cdot \vec{e_z} \\ \)

Durch Differenzieren nach der Eigenzeit kommen wir dann zu:

Vierer-Geschwindigkeit: \( \vec{U} = \Large \frac{d\vec{S}}{d\tau} \)

Vierter-Impuls: \( \vec{P} = m \cdot \vec{U}  \)

Vierer-Beschleunigung: \( \vec{A} = \Large \frac{d^2\vec{S}}{d\tau^2} = \frac{d\vec{U}}{d\tau} \)

Vierer-Kraft: \( \vec{F} = \Large \frac{d\vec{P}}{d\tau} = m \cdot \vec{A} \)

Wie differenziere ich nun nach der Eigenzeit?

Vierer-Geschwindigkeit:

\( \Large \vec{U} =\frac{d\vec{S}}{d\tau} = \frac{d}{d\tau}(   ct \cdot \vec{e}_t +  x \cdot \vec{e}_x  + y \cdot \vec{e}_y + z \cdot \vec{e}_z    ) \)

In einem Inertialsystem sind die Basisvektoren konstant; d.h. die Ableitungen auch nach τ sind Null. Damit vereinfacht sich die Produktregel und wir erhalten:

\( \Large \vec{U} = \frac{d\vec{S}}{d\tau} = c \frac{dt}{d\tau} \vec{e}_t + \frac{dx}{d\tau} \vec{e}_x + \frac{dy}{d\tau} \vec{e}_y + \frac{dz}{d\tau} \vec{e}_z \)

Penrose-Diagramme

So ein Raum-Zeit-Diagramm nach Minkowski benutzt ja eine unendliche Ebene zur Darstellung. Durch eine geeignete Koordinatentransformation können wir so eine unendliche Ebene auf eine endliche Figur abbilden…

Roger Penrose (*1931)

Tangens

 

 

Mathematik: Was sind Tensoren?

dkracht

Gehört zu: Mathematik
Siehe auch: Quantenmechanik,  Vektorräume, Lineare Algebra, Koordinatensysteme, Metrik-Tensor, Kontravariante Ableitung
Benutzt: WordPress-Plugin Latex

Stand: 26.10.2021

Was sind Tensoren?

Eine der Voraussetzungen zum Verständnis vieler Dinge (z.B. in der Allgemeinen Relativitätstheorie und der Quantenmechanik) sind sog. Tensoren.

Der Begriff “Tensor” wurde im 19. Jahrhundert relativ unsystematisch bei verschiedenen physikalischen Berechnungen eingeführt.

Darüber gibt es schöne Youtube-Videos von “eigenchris”:  https://youtu.be/sdCmW5N1LW4

Als Vorbereitung dazu habe ich zuerst mal etwas zu Vektorräumen zusammengestellt.

Auffrischung

Wir hatten ja im Artikel über Vektorräume schon gesehen, dass Vektoren Objekte sind, die unabhängig von Koordinatensystemen exsistieren und auch gegenüber einem Wechsel von Koordinatensystemen “invariant” sind. Nur die Komponenten bzw. Koordinaten der Vektoren verändern sich dann, nicht aber die Vektoren selber.

Invarianz bedeutet allgemein gesagt, dass ein und dasselbe Objekt verschieden beschrieben (“repräsentiert”) werden kann von verschiedenen Standpunkten (Koordinatensystemen) aus.

Unsere Vektorkomponenten beruhen immer auf einer Menge von sog. Basisvektoren.

Wie verhalten sich dann Vektoren und ihre Komponenten bei einem Wechsel der Basisvektoren?

Im Gegensatz zum invarianten Vektor selbst, verändern sich seine Komponenten bei Änderung der Vektorbasis.

Wir sahen, dass wenn sich die Längen der Basisvektoren verlängern, sich die Komponenten von Vektoren verkleinern. Deshalb hatten wir diese Vektoren “kontravariant” genannt.

So ein kontravarianter Vektor ist ein erstes Beispiel für einen Tensor. Ein zweites Beispiel für einen Tensor sind die sog. Co-Vektoren…

Allgemein gesagt bedeutet Kontravarianz, dass wenn ein Ding größer wird, ein anderes Ding kleiner wird. Kovarianz dagegen bedeutet, dass die Veränderungen in die gleiche Richtung gehen.

Co-Vektoren

Im Gegensatz zu den “herkömmlichen” kontravarianten Vektoren, die wir als Spalte schreiben, schreiben wir Co-Vektoren als Zeilen.

Dazu hat “eigenchris” ein schönes Youtube-Video gemacht: https://youtu.be/LNoQ_Q5JQMY

In der Sichtweise von Koordinaten macht ein Co-Vektor also folgendes:

\( \Large  \left[  \begin{matrix} a & b & c  \end{matrix} \right] \cdot \left[ \begin{array}{r} x \\\ y \\\ z  \end{array} \right] = ax+by+cz \)

Abstrakt formuliert bildet ein Co-Vektor also Vektoren auf Skalare ab.

Rank 2 Tensoren

Generell soll ein Tensor ja invariant bei einer Koordinatentransformation sein.

Lediglich die “Darstellung” eines Tensors erfolgt mit Komponenten (Koordinaten).

Uns interessieren hier in erster Linie sog. Rank 2 Tensoren. Solche Rank 2 Tensoren können immer als “normale” Matrix mit Zeilen und Spalten dargestellt werden  (Zeilen und Spalten -> Rank 2). So ein Rank 2 Tensor kann aber auch ganz einfach in sog. Index-Schreibweise dargestellt werden z.B. Tij oder g μν (Anzahl Indices = Rank).

Transformationsverhalten

xyz

 

 

Computer: Mathematik – Vektorräume – Lineare Algebra

dkracht

Gehört zu: Mathematik
Siehe auch: Grundlagen,  Algebren, Matrizenrechnung, Tensor-Algebra, Relativitätstheorie, Metrik-Tensor,  Elektrisches Feld, Magnetisches Feld
Benutzt: WordPress-Plugin Latex

Stand: 27.11.2022  (Drehmoment, Archimedes, Skalarprodukt, Vektorbasis)

Youtube-Videos zur Vektor- und Tensorrechnung (für Physiker)

Youtube Videos von Prof. Wagner zur Vektor- und Tensorrechnung

  • VT I – 01 Affine und Euklidische Vektorräume:https://www.youtube.com/watch?v=NxQTRW-5vpk
  • VT I – 02 Inhalt und Winkel:https://www.youtube.com/watch?v=1cyrZZnhjjs
  • VT I – 03 Vektorbasen und Vektorkomponenten:https://www.youtube.com/watch?v=BD-Xb9Wj0I8
  • VT I – 04 Ko- und Kontravariante Vektorbasen:https://www.youtube.com/watch?v=XBMRx4rXPPg
  • VT I – 05 Anwendungen des Metriktensors:https://www.youtube.com/watch?v=okkfJEeEqk4
  • VT I – 06 Transformation zwischen Basen – Beispiele:https://www.youtube.com/watch?v=iieCaxYj2RQ
  • VT II – 01 Differentialoperatoren:https://www.youtube.com/watch?v=0tjWWS2DGmU&t=127s
  • VT II – 02 Anschauliche Interpretation der Differentialoperatoren:https://www.youtube.com/watch?v=Cyqahzn-cXw&t=3s
  • VT II – 03 Anwendungsbeispiele für Differtialoperatoren:https://www.youtube.com/watch?v=DfPGExmGRrs
  • VT II – 04 Kurven und Hyperflächen:https://www.youtube.com/watch?v=c07r4pARzHw
  • VT II – 05 Krummlinige Koordinaten:https://www.youtube.com/watch?v=yQlbJN8I6kk
  • VT II – 06 Krummlinige Koordinaten – Beispiele:https://www.youtube.com/watch?v=s1E_XeIgCpI&t=545s
  • VT II – 07 Transformationsverhalten, Tensoren:https://www.youtube.com/watch?v=srGlFECRijo&t=928s
  • VT II – 08 Bogenlänge von Kurven, Metrik:https://www.youtube.com/watch?v=2FCEKDMnKew&t=2075s
  • VT II – 09 Kovartiante Ableitung, Christoffel Symbole:https://www.youtube.com/watch?v=OnR5Ny47IXw
  • VT II – 10 Beispiele zur kovarianten Ableitung:https://www.youtube.com/watch?v=jQjsEK7GAVY
  • VT II – 11 Vektor-Differentaloperatoren in krummlinigen Koordinaten:https://www.youtube.com/watch?v=7PXs4_9RHWo&t=107s
  • VT II – 12 Eigenschaften der kovarianten Ableitung, Riemannscher Krümmungstensor:https://www.youtube.com/watch?v=I-OAGrUX580&t=429s
  • VT II – 13 Vom Riemannschen Krümmungstensor zu den Einsteinschen Feldgleichungen:https://www.youtube.com/watch?v=NqiV8SCtHCA&t=203s
  • VT II – 14 Geodätische Linien, Parallele Vektoren:https://www.youtube.com/watch?v=TfeTfqLa8vI

Vektorfelder und Skalarfelder

Was meint man mit dem Begriff “Feld”?

Das Wort “Feld” wird gerne gebraucht, wenn eigentlich eine ganz normale Abbildung (auch Funktion oder auch Verknüpfung genannt) gemeint ist – “just to confuse the Russians”.

Der Definitionsbereich so einer Abbildung ist ein “Raum”. Das kann ein sog. Euklidischer Raum oder auch eine Riemannsche Mannigfaltigkeit sein. Die Punkte (Orte) in so einem Raum kann man durch Koordinaten beschreiben.
Je nach dem ob der Wertebereich ein Vektorraum oder ein Körper (von Skalaren) ist, spricht man von “Vektorfeld” oder “Skalarfeld” und man schreibt gerne:

  • für ein skalares Feld: \( \Phi(r) \)
  • für ein Vektorfeld: \(  \vec{V}(r) \)

Wobei r ein Punkt aus dem Definitionsbereich ist (kein Vektor, sondern ein durch Koordinaten beschriebener Punkt)

Beispiele

  • Temperatur: Wenn wir jedem Punkt im Raume seine Temperatur zuordnen, haben wir ein Skalarfeld.
  • Höhe: Wenn wir jedem Punkt auf einer Landkarte die Höhe über dem Meeresspiegel zuordnen, haben wir ein Skalarfeld.
  • Wind: Wenn wir jedem Punkt auf einer Landkarte die Windrichtung und Windstärke zuordnen, haben wir ein Vektorfeld.
  • Gravitation: Wenn wir jedem Punkt im Raum die Richtung und Stärke der Gravitationskraft zuordnen (wäre mit einem kleinen Probekörper zu bestimmen), haben wir ein Vektorfeld, genannt Gravitationsfeld
  • Ein elektrisches Feld (ein Vektorfeld) gibt für jeden Punkt im Raum die Richtung und Stärke der elektrischen Kraft an, die auf ein kleines Probeteilchen der elektrischen Ladung +1 wirkt
  • Ein magnetisches Feld (ein Vektorfeld) gibt für jeden Punkt im Raum die Richtung und Stärke der magnetischen Kraft an, die auf ein kleines Probeteilchen wirkt

Visuelle Veranschaulichung von Feldern

Skalarfelder kann man beispielsweise durch Linien im Definitionsbereich, die alle einen gleichen Skalarwert haben, veranaschaulichen (z.B. Isotermen, Isohypsen etc.)

Vektorfelder veranschaulicht man sich gerne durch sog. “Feldlinien“; diese zeigen dann immer in die Richtung des Werte-Vektors. Beispiel: Feldlinien im Magnetfeld, die in Richtung der magnetischen Kraft zeigen…

Die Physiker sprechen gern von sog. Kraftfeldern. Der Begriff “Feld” hilft, die Vorstellung der Fernwirkung zu vermeiden (sagt Feynman). Die vier konzeptionellen Stufen der Kraftwirkung sind:

  • Die Kraft bewirkt eine Beschleunigung   (Newton)
  • Ein Feld bewirkt eine Kraft
  • Kraft durch Raumkrümmung (geometrische Vorstellung) (Einstein)
  • Kraft durch virtuelle Austauschteilchen

Eigenvektoren und Eigenwerte

Bei Linearen Abbildungen in den gleichen Vektorraum, also:

\(  f: V  \to V \\\)

sind Eigenvektoren dieser Linearen Abbildung Vektoren, die durch diese Abbildung nicht in ihrer Richtung verändert werden; d.h.:

\(  f(\vec{x}) = \lambda \vec{x} \\\)

und den Skalar λ nennt man dann den Eigenwert.

Häufig verwendet man Eigenvektoren und Eigenwerte, wenn die Lineare Abbildung durch eine Matrix beschrieben wird.

In der Quantenphysik spielt dies Konzept eine wichtige Rolle. Dort werden Eigenwerte als Messwerte bei einem Experiment interpretiert.

Das Skalarprodukt von Vektoren

Auf einem Vektorraum kann ein Skalarprodukt definiert sein (Vektor mal Vektor ergibt einen Skalar) –  Dies ist inspiriert aus der Physik durch Arbeit = Kraft mal Weg.

Vektorräume müssen aber nicht notwendig ein Skalarprodukt haben.

Wir werden sehen, dass so ein Skalarprodukt dann eine “Norm” induziert und damit eine Metrik, wodurch z.B. Grenzwertprozesse möglich werden.

Einen \(\mathbb{R}\)-Vektorraum mit Skalarprodukt nennt man auch einen Euklidischen Raum, einen \(\mathbb{C}\)-Vektorraum mit Skalarprodukt nennt man auch Hilbertraum – genauer Prähilbertraum.

Das innere Produkt zweier Vektoren v und w (auch Skalarprodukt oder Dot Product genannt) ist schreibt man:

\( \Large \vec{v} \cdot \vec{w} \) \( \Large \langle v,w \rangle \)

Definition des inneren Produkts

Man kann das innere Produkt geometrisch und anschaulich definieren oder aber auch mathematisch über Axiome.

Geometrische Definition

Unabhängig von einem Koordinatensystem – geometrisch definiert als:

\( \Large \vec{v} \cdot \vec{w} = ||  \vec{v} || \enspace || \vec{w} || \cos(\angle \left( \vec{v}, \vec{w} \right)) \)

Als Schlussfolgerung kann man die Länge eines Vektors auch per innerem Produkt darstellen als:

\( \Large || \vec{v} ||  = \sqrt{\vec{v} \cdot \vec{v}} \\\ \)

In einem chartesischen Koordinatensystem (s.u.) berechnet sich das innere Produkt (Skalarprodukt) der Vektoren

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right]  \) und   \( \Large \vec{w} = \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right]  \)

als   \( \Large \vec{v} \cdot \vec{w} = v_1 w_1 + v_2 w_2 + v_3 w_3 \)

Soweit haben wir das innere Produkt (Skalarprodukt) zweier Vektoren durch Winkel und Länge anschaulich definiert. Wir können auch umgekehrt Länge und Winkel durch das Skalarprodukt definieren:

Länge:

\( \Large || \vec{v} ||  = \sqrt{\vec{v} \cdot \vec{v}} \\\ \)

Winkel:

\( \Large \cos(\angle \left( \vec{v}, \vec{w} \right))  = \frac{ ||  \vec{v} || \enspace || \vec{w} ||}{ \vec{v} \cdot \vec{w}    }  \)

Das funktioniert aber nur, wenn wir schon ein Skalarprodukt haben.

Sprechweise: Tensoren statt Vektoren und Matrizen

Die Tensoren und die Tensorrechnung stammen eigentlich aus der Physik und sind für ganz praktische physikalische Problemlösungen “erfunden” worden. Ein Tensor in diesem Sinne ist einfach ein indiziertes Objekt. Die Indizes laufen normalerweise von 1 bis n, der Dimensionszahl des Raumes in dem wir arbeiten.

Ein Objekt mit einem Index wäre ein Tensor der Stufe 1, ein Objekt mit zwei Indizes ein Tensor 2. Stufe etc. Die “Objekte”, die man indiziert sind meist Reelle oer Komplexe Zahlen – allgemein gesagt Elemente eines Körpers – die man auch Skalare nennt.

Einen Tensor 1. Stufe schreibt man gerne \( a_i \) also mit einem Index – meist unten aber manchmal auch oben \( a^i \) .

Man kann so einem Tensor 1. Stufe auch einen Vektor zuordnen, wobei die indizierten Größen dann die Komponenten eines Vektors zu einer bestimmten Vektorbasis (s.u.) werden. Wenn man so einen Vektor meint, schreibt man das Ganze in Klammern – womit dann alle Komponenten des Tensors gemeint sind:

\( (a_i)  \)

Einen Tensor 2. Stufe schreibt man gerne \( {a_i}^j \) also mit zwei Indizes – teilweise unten und teilweise auch oben.

Man kann so einem Tensor 2. Stufe auch eine Matrix zuordnen, wobei die indizierten Größen dann als Zeilen und Spalten in der Matrix abgelegt werden. Wenn man so eine Matrix meint, schreibt man das Ganze in Klammern (da sind dann eben alle Komponenten drin):

\( ({a_i}^j) \\\ \)

Bei mehreren Indizes (also Tensoren der Stufe 2 und höher) ist es wichtig, dass die Reihenfolge der Indizes immer ersichtlich ist. Verwechselungsgefahr besteht ja speziell wenn man Indizes unten und oben hinschreibt.

Wenn ich zwei Tensoren 2. Stufe habe, kann ich die zugehörigen Matrizen ganz einfach multiplizieren indem wir mit der Einsteinschen Summenkonvention über den inneren Index (hier j) summieren:

\( ({a_i}^j)({b_j}^k) = ({a_i}^j \cdot {b_j}^k) \)

=========================================

Eigenschaften von Vektoren

Aus geometrischer und intuitiver Sicht spricht man auch von Längen und Winkeln:

  • Für die Länge eines Vektors (man sagt auch “Norm”) schreibt man:  \( \Large ||  \vec{v}  ||  \)
  • Für den Winkel zwischen zwei Vektoren schreibt man: \( \Large  \angle \left( \vec{v}, \vec{w} \right)  \)

Das äußere Produkt von Vektoren

Das äußere Produkt zweier Vektoren (auch Vektorprodukt oder Kreuzprodukt genannt) ist definiert als ein Vektor:

\( \Large \vec{v} \times \vec{w} = \vec{u} \)

Der Vektor u steht senkrecht auf beiden Vektoren v und w und hat die Länge \( \Large ||\vec{v}|| \cdot ||\vec{w}|| \cdot \sin(\angle \left( \vec{v}, \vec{w} \right)) \)

In einem chartesischen Koordinatensystem (s.u.) berechnet sich das äußere Produkt (Vektorprodukt) der Vektoren

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right]  \) und   \( \Large \vec{w} = \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right]  \)

als   \( \Large   \vec{v} \times \vec{w} =   \left[ \begin{array}{c} v_2 w_3 – v_3 w_2  \\\ v_3 w_1 – v_1 w_3  \\\ v_1 w_2 – v_2 w_1  \end{array} \right]        \)

Anwendungen

Eine Anwendung für das Kreuzprodukt ist beispielsweise die Kreisbewegung, wo sich die Bahngeschwindingkeit aus Winkelgeschwindigkeit ω und Radius r wie folgt ergibt:

\( \vec{v} = \vec{\omega} \times \vec{r} \\ \)

Bei der Rotation ergibt sich das sog. Drehmoment \(\vec{M}\)  aus dem Kraftvektor \(\vec{F}\) und dem Ortsvektor \( \vec{r} \) vom Bezugspunkt zum Angriffspunkt der Kraft:

\( \vec{M} = \vec{r} \times \vec{F} \)

Hierin steckt auch das aus der Schulzeit bekannte Hebelgesetz (Archimedes von Syrakus 287 v.Chr. – 212 v.Chr.): Kraft mal Kraftarm = Last mal Lastarm

Algebren

Ein Vektorraum V über einem Körper K zusammen mit einer bilinearen Abbildung:

\(  V \times V \to V \)

wird eine Algebra genannt.

Die bilineare Abblidung wird “Produkt” genannt und auch so wie ein Produkt hingeschrieben; also:  a · b  oder einfach ab. In dieser Schweibweise bedeutet die Bilinearität einfach folgendes:

\(   (x + y) \cdot z = x \cdot z + y \cdot z  \\\ \)

 

\(   x \cdot (y + z)  = x \cdot y + x \cdot z  \\\ \)

 

\( a (x \cdot y) = (ax) \cdot y = x \cdot (ay) \\\ \)

Das “besondere” an Algebren ist die “Multiplikation”. Deswegen unterscheidet man  Algebren auch nach den Eigenschaften dieser Multiplikation:

Kommutative – nicht-kommutative Algebren: Ist immer \( a \cdot b  =  b \cdot a \) oder nicht?

Assoziative – nicht-assoziative Algebren: Ist immer \( a \cdot (b \cdot c) = (a \cdot b) \cdot c \) oder nicht?

Beispiele:

Die n × n Matrizen über einem Körper mit der gewöhnlichen Matrizenmultiplikation als “Multiplikation” bilden eine (assoziative) Algebra.

Hilbertraum und Operatoren

Ein Vektorraum über \(\mathbb{R} \) oder \(\mathbb{C} \) mit einem Skalarprodukt heisst “Prä-Hilbertraum”. Wenn so ein “Prä-Hilberraum” auch noch “vollständig” ist; d.h. jede Cauchy-Folge konvergiert (bezüglich der Metrik), dann hat man einen echten Hilbertraum; Nach David Hilbert (1862-1943).

Abbildungen von einem Hilbertraum in sich selbst heissen auch “Operatoren“.

Beispiel: Differentialoperatoren

Koordinatensystem, Dimension

In einem Vektorraum V kann ich viele Koordinatensysteme haben. Jedes Koordinatensystem ist bestimmt durch eine Menge sog. Basis-Vektoren.

Dann kann jeder Vektor des Vektorraums als sog. Linearkombination aus den Basis-Vektoren dargestellt werden kann. Eine solche “Linearkombination” ist eine Summe von Basis-Vektoren, die mit geeigneten Skalaren multipliziert wurden.

Beispiel für eine Linearkombination:

\( \Large a  \vec{v} + b \vec{w} + c \vec{u} \)

Ganz genau genommen, spannt eine Basis nicht nur den ganzen Vektorraum auf (das wäre ein Erzeugendensystem), sondern enthält dabei eine minimale Anzahl von Vektoren (was äquivalent ist mit der eindeutigen Darstellung aller Vektoren des Vektorraums in Form von Linearkombinationen).

Beispiel für eine Basis (im Vektorraum \(\mathbb{R}^3\) ):

\( \hat{i} =\left[ \begin{array}{c} 1 \\\ 0 \\\ 0  \end{array} \right]   \hat{j} =\left[ \begin{array}{c} 0 \\\ 1 \\\ 0  \end{array} \right] \hat{k} =\left[ \begin{array}{c} 0 \\\ 0 \\\ 1  \end{array} \right] \)

Und man schreibt dann auch gerne:

\( \Large \vec{v} = \left[ \begin{array}{c} x \\\ y \\\ z  \end{array} \right] = x \hat{i} + y \hat{j} + z \hat{k}\)

Ein Vektorraum kann mehrere Basen haben, die jeweils ein Koordinatensystem definieren. Dabei werden die Koordinaten (Komponenten) ein und desselben Vektors in verschiedenen Koordinatensystem auch verschieden sein, der Vektor selbst aber ist “invariant”. Wenn man einen Vektor als Liste von Koordinaten hinschreibt, muss man immer sagen. welche Basis gemeint ist.

Ein Vektorraum kann mehrere Basen haben, aber die Anzahl der Vektoren in einer Basis ist immer die gleiche. Diese Anzahl nennt man “Dimension” des Vektorraums und schreibt:

Dimension des Vektorraums V: dim(V)

Beschreibung durch Basis-Vektoren: Lineare Transformationen

Eine Lineare Transformation kann eindeutig beschrieben werden durch die Werte auf die die Basis-Vektoren abgebildet (transformiert) werden.

Beispielsweise heisst das im Vektorraum \(\mathbb{R}^2\) mit dem kanonischen Koordinatensystem und den Basisvektoren \( \hat{i} \) und \( \hat{j}  \) folgendes:

Wenn wir einen Vektor \( \vec{v} = \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x \hat{i} + y\hat{j} \) betrachten, so wirkt eine Lineare Transformation L wie folgt:

\( L(\vec{v}) = x L(\hat{i}) + y L(\hat{j} )  \)

Wenn wir also die transformierten Basisvektoren \( L(\hat{i}) \) und \( L(\hat{j}) \)  kennen, ist damit die Lineare Transformation L vollständig festgelegt.

Diese transformierten Basis-Vektoren können im verwendeten Koordinatensystem als Matrix schreiben.

Wenn bei unserer Linearen Transformation beispielsweise \( L(\hat{i}) = \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] \)   und \( L(\hat{j}) = \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] \)  wäre, bekämen wir eine Matrix:

\(\left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right] \)

Wir schreiben also in den Spalten der Matrix die transformierten Basisvektoren.
Die Lineare Transformation könnte im benutzten Koordinatensystem als Matrixmultiplikation aufgefasst werden:

\(\left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right]  \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x  \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] + y  \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] = \left[ \begin{array}{c} 3x+2y \\\ -2x+1y  \end{array} \right]\)

Völlig analog werden auch Lineare Transformationen in drei oder mehr Dimensionen behandelt.

Beschreibung durch Basis-Vektoren: Wechsel von Koordinatensystemen

Wenn wir zwei Koordinatensysteme betrachten, dann haben die also zwei Basen (wir nennen sie “alte Basis” und “neue Basis”). Intuitiv ist klar, dass wenn die neue Basis z.B. längere Basisvektoren hat, dann sind die Vektorkomponenten kürzer (weil ja der gleiche Vektor wieder herauskommen soll). Die Vektorkomponenten verhalten sich also “umgekehrt” wie die Längen der Basisvektoren. Deshalb nennt man diese Vektoren “kontravariant“.

Wir können das auch haarklein ausrechnen:

  • Die “alte Basis” sei: \( \vec{e}_i  \)
  • Die “neue Basis” sei: \( \tilde{\vec{e}}_i  \)

Dann transformieren sich die Basisvektoren wie folgt:

Alt -> Neu (“Foreward”):

\(  \tilde{\vec{e}}_i =  \sum\limits_{k=1}^{n} F_{ki} \vec{e_k}\)

Neu -> Alt (“Backward”):

\(  \vec{e}_i =  \sum\limits_{j=1}^{n} B_{j i} \widetilde{\vec{e_j}}\)

Für die Komponenten eines Vektors \( \vec{v} \) gilt dann die umgekehrte Richtung (deshalb nennt man sie “kontravariant“)

Alt -> Neu:

\( \tilde{v_i} = \sum\limits_{j=1}^{n} B_{ij} v_j  \)

Neu -> Alt

\( v_i = \sum\limits_{j=1}^{n} F_{ij}\tilde{v_j}   \)

Berechnung der Länge eines Vektors aus seinen Komponenten

Länge eines Vektors im Chartesischen Koordinatensystem

Wir sind ja gewöhnt, die Länge eines z.B. dreidimensionalen Vektors über seine Koordinaten und den Lehrsatz des Pythagoras zu berechnen:

Im Beispiel sei der Vektor \( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] \)

Dann wäre die Länge dieses Vektors gegeben durch: \( || \vec{v} ||= \sqrt{v_1^2 + v_2^2 + v_3^2} \)  (der gute alte Pythagoras)

In verschiedenen Koordinatensystemen würde dieser Vektor aber mit verschiedenen Koordinaten (Komponenten) beschrieben und es würden mit obiger Formel dann unterschiedliche Längen heraus kommen.

Uns ist ja klar, dass wir zu den Koordinaten (Komponenten) eines Vektors auch immer angeben müssen, in welchem Koordinatensystem diese gemessen werden; d.h. wir müssen zu den Koordinaten die dazugehörige Basis angeben – und berücksichtigen.

Wenn wir als Basis allgemein schreiben: \( \vec{e}_i  \)

dann können wir mit den Komponenten unseres Vektors zu dieser Basis schreiben:

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] = v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3\)

Im Spezialfall der orthonormalen Basis:

\( \vec{e}_1 = \hat{i}, \vec{e}_2 = \hat{j}, \vec{e}_3 = \hat{k}   \)

hätten wir die Länge unseres Vektors nach Pythagoras (s.o.); mit den Koordinaten zu einer anderen Basis müssten wir umrechnen…

Länge eines Vektors in einem beliebigen Koordinatensystem

Wir hatten die Länge eines Vektors unabhängig von einem Koordinatensystem (also invariant) definiert über:

\( \Large {||  \vec{v}  ||}^2 = \vec{v} \cdot \vec{v} \\\)

Wir nehmen jetzt ein beliebiges Koordinatensystem definiert durch seine Basisvektoren \( \vec{e}_i\).
Dann können wir die Länge des Vektors wie folgt aus seinen Komponenten (Koordinaten) berechnen:

\( \Large  ||  \vec{v} ||^2 = (v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3) \cdot(v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3) \\ \)

Wenn wir das ausmultiplizieren bekommen wir:

\( \Large ||  \vec{v} ||^2 =  \sum\limits_{ij} v_i v_j  \enspace \vec{e}_i \cdot \vec{e}_j \\ \)

Um die Länge eines Vektors in einem beliebigen Koordinatensystem zu ermitteln, benötigen wir also “lediglich” alle Kombinationen der inneren Produkte der Basisvektoren dieses Koordinatensystems; d.h. alle \( \vec{e}_i \cdot \vec{e}_j \)

Als Matrix können wir diese Produkte so hinschreiben:

\(\Large g =  \left[ \begin{array}{rrr} \vec{e}_1 \cdot \vec{e}_1 & \vec{e}_1 \cdot \vec{e}_2 & \vec{e}_1 \cdot \vec{e}_3\\  \vec{e}_2 \cdot \vec{e}_1 & \vec{e}_2 \cdot \vec{e}_2 & \vec{e}_2 \cdot \vec{e}_3 \\  \vec{e}_3 \cdot \vec{e}_1 & \vec{e}_3 \cdot \vec{e}_2 & \vec{e}_3 \cdot \vec{e}_3 \end{array} \right]  \\\)

Diese Matrix g nennt man auch den Metrik-Tensor des Koordinatensystems.

Mit Hilfe dieses Metrik-Tensors ergibt sich dann die Länge des Vektors \(\vec{v}\) ganz einfach als Matrixprodukt:

\(\Large || \vec{v} ||^2  =  \left[ \begin{array}{c} v_1 & v_2 & v_3  \end{array} \right]  g  \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] \\\)

Ganz allgemein kann man mit diesem Metrik-Tensor das innere Produkt zweier Vektoren aus den Komponenten berechnen:

\( \Large \vec{v} \cdot \vec{w} =  \left[ \begin{array}{c} v_1 & v_2 & v_3  \end{array} \right]  g  \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right] \)

Das funktioniert, weil der Metrik-Tensor nicht “irgendeine” Matrix ist, sondern “invariant” ist; d.h. unabhängig vom gewählten Koordinatensystem kommt immer das gleiche Ergebnis heraus.

Der Metrik-Tensor

Der Metrik-Tensor definiert also eine (bilineare) Abbildung:

\(  g: V \times V \to \mathbb{R} \\\)

Ein Metrik-Tensor ist eine spezielle Bilineare Abbildung, die erstens symmetrisch ist und zweitens immer positive Werte liefert.

Dies ist auch im Prinzip der Metrik-Tensor, der in den Einsteinschen Feldgleichungen als \( g_{\mu \nu} \) vorkommt.

Oben hatten wir das innere Produkt zweier Vetoren ja versucht unabhängig von einem Koordinatensystem zu definieren.
Man kann das Ganze nun aber auch umgekehrt “aufzäumen”.  Wenn wir einen Vektorraum und eine Basis haben (damit also ein Koordinatensystem), brauchen wir nur noch einen Metrik-Tensor “g” und können damit ein inneres Produkt zwischen zwei Vektoren v und w als schlichte Matrix-Multiplikation definieren:

\( \Large \vec{v} \cdot \vec{w} =  \vec{v}^T   \enspace g  \enspace \vec{w} \\ \)

Wobei das hochgestellte T “transponiert” meint. So wird aus einem Spaltenvektor ein Zeilenvektor.

Beispielsweise definiert der folgende Metrik-Tensor die übliche Metrik für alle Koordinatensysteme mit einer orthonormaler Basis – denn das innere Produkt verschiedener Basisvektoren ist Null (weil orthogonal) und das innere Produkt eines Basisvektors mit sich selbst ist 1 (weil Länge 1):

\(\Large g =  \left[ \begin{array}{rrr} 1 & 0 & 0\\  0 & 1 & 0 \\  0 & 0 & 1 \end{array} \right]  \\\)

Das gilt z.B. für ein “normales” Koordinatensystem im Euklidischen Raum.
Mit dieser Metrik ist die Länge eines Vektors also:
\( || \vec{v} ||^2 = v_1^2 + v_2^2 + v_3^2 \)
und diese Länge ist invariant gegenüber Koordinatentransformationen.

Und eine Minkowski-Metrik wird definiert durch den Metrik-Tensor:

\(\Large \eta =  \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0\\  0 & -1 & 0  & 0\\  0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array} \right]  \\\)

Mit dieser Metrik wäre die Länge eines Vektors also gegeben durch:

\( || \vec{v} ||^2  =  v_1^2 – v_2^2 – v_3^2 – v_4^2\)

Diese so definierte Länge wäre invariant gegenüber Lorentz-Transformationen, die wir später in der Speziellen Relativitätstheorie kennenlernen werden.

Was ist ein Tensor?

Der oben beschriebene Metrik-Tensor ist ein Tensor vom Rank 2. D.h. eine zweidimensionale (also “normale”) Matix, die sich bei Transformation der Koordinatensysteme “freundlich” verhält, sodass wir von “Invarianz” sprechen können.

Allgemein und formal ist ein Tensor T eine multilineare Abbildung von einem cartesischen Produkt von Vektorräumen über einem gemeinsamen Körper von Skalaren in diesen Skalaren-Körper:

\( T: V_1 \times V_2 \times … \times V_n \to K \)

Wobei die \(V_i\) Vektorräume über K sind.

Das allgemeine Thema “Tensor” ist mathematisch vielschichtig, deshalb habe ich begonnen, einen separaten Artikel darüber zu geschrieben.

Link: https://youtu.be/8ptMTLzV4-I

Determinante und Rank

Diese Konzepte werden in Video 6 und Video 7 behandelt.

Bei einer Linearen Transformation wird die Fläche des Quadrats aus den Basisvektoren  um einen Faktor “transformiert”. Damit wird auch jede beliebige Fläche um diesen Faktor “transformiert”. Diesen “Faktor” nennen wir die Determinante der Linearen Transformation.

Entsprechend ist das auch in höheren Dimensionen z.B. mit drei Dimensionen, wo die Größe des Volumens transformiert wird.

Eine negative Determinante bedeutet, dass sich bei der linearen Transformation die “Orientierung” des Vektorraums umkehrt.

Der Rank meint die Dimension des Ausgaberaums einer Linearen Transformation. Wenn der Rank einer Transformation nicht die volle Dimension (“full rank”) unseres Vektorraums ist, ist die Determinante dieser Transformation natürlich Null, aber der Rank kann etwas differenzierter aussagen was da los ist z.B. der Rank einer 3-dimensionalen Matrix (Transformation) könnte 2 sein, dann ist der Ausgaberaum eine Ebene (2 Dimensionen), wenn der Rank 1 wäre, hätten wir als Ausgaberaum eine Linie (eine Dimension) etc. Dieser “Ausgaberaum” wird auch “Column Space” genannt, weil die Spaltenvektoren diesen aufspannen…

 

Computer: Mathematik – Statistik

dkracht

Mathematik: Statistik (aus Wiki)

Immer wieder werde ich als gelernter Mathematiker nach elementaren Themen der Statistik gefragt.

Ich habe einen schönen Einführungskurs in die Statistik bei der Universität Newcastle, Australien, gefunden:

http://www.anu.edu.au/nceph/surfstat/surfstat-home/t-table.html

http://www.anu.edu.au/nceph/surfstat/surfstat-home/

Statistik

Typen von Variablen (“Metriken”)

Qualitativ / Quantitativ

Man spricht von “qualitativen” Variablen, wenn die Beobachtungen durch Kategorien beschrieben werden.
Beispiele:

  • Augenfarbe: braun, grau, blau,…
  • Delivery Model: insourced, outsourced
  • Performance Rating: Less than Acceptable, Inconsistent, Fully Successful, Exceeds, Exceptional

Eine qualitative Variable heist “ordinal”, wenn es eine natürliche Reihenfolgebeziehung zwischen den Kategorien gibt, (Beispiel: Performance Rating).

Eine qualitative Variable heisst “nominal”, wenn es keine natürliche Reihenfolgebeziehung gibt, (Beispiel: Augenfarbe).

Man spricht von “quantitativen” Variablen, wenn die Beobachtungen durch numerische Werte beschrieben werden, d.h. durch Zählen oder Messen zustande kommen.
Beispiele:

  • Alter
  • Körpergröße
  • Anzahl Personen im Haushalt
  • Anzahl gerauchter Zigaretten am Tag
  • Einkommen im Jahr

Eine quantitative Variable heisst “diskret”, wenn die Beobachtungen ganzzahlige Werte sind (Beispiel: Anzahl Personen im Haushalt).

Eine quantitative Variable heisst “stetig” (continous), wenn sie durch (im Prinzip) beliebige Zahlen dargestellt wird (Beispiel: Körpergröße).

Normalverteilung mit Perzentil

Fragestellung zu einer Normalverteilung N(My,Sigma):

  • Gegeben sei My und P25
  • Gesucht ist Sigma
  • Lösung: sigma = (P25 – My) / NormInv(0,25; 0; 1)

Im übrigen gilt sowieso: P25 = NormInv(0,25; My; Sigma)

Logarithmische Normalverteilung

Zur Logarithmischen Normalverteilung habe ich einen gesonderten Artikel geschrieben.

Beta-Verteilung

Zur Beta-Verteilung habe ich einen gesonderten Artikel geschrieben.

— Dkracht 12:29, 24 March 2008 (CET)