Gehört zu: Astronomie (this is the root article)
Siehe auch: Physik
Stand: 29.06.2025
Google Drive / pCloud
- pCloud: 20240815 Astrofotografie Eimsbuettel.pptx
- pCloud: 20240815 Astrofotografie Eimsbuettel.pptx
- pCloud: 20240930 Die Namen der Sterne.pptx
- pCloud: 20250208 Adaptive Optik.pptx
- pCloud: 20250329 Sonnenfinsternis_v3.pptx
YouTube
- Platesolving mit Siril: https://youtu.be/Qs3_jdZ6-uE?si=N0egB4T_ztCshhdT
- Astronomische Helligkeiten: https://youtu.be/rzBTMLCKpPg?si=m75jfUQJ1k-NKp2N
- Polar Alignment: https://youtu.be/ZpzU4mYKHYU?feature=shared
- Fokussieren: https://youtu.be/07n__dgjUAQ?feature=shared
- Plate Solving: https://youtu.be/koPUnr-eMRM?feature=shared
- Pointing und Framing: https://youtu.be/K1AzaI5jY6I?feature=shared
- Computersteuerung: https://youtu.be/5D_3X6FI2O8?feature=shared
- Autoguiding: https://youtu.be/YYorQPiyeK4?feature=shared
Und:
- Hertzsprung-Russel-Diagramm: https://youtu.be/IqUlcjItM1Q?feature=shared
- Analemma und Zeitgleichung: https://youtu.be/M4oKCe_RoR4?feature=shared
- Goto mit Cartes du Ciel: https://youtu.be/cs38xauslJs?feature=shared
- ASCOM-Teleskopsteuerung mit Cartes du Ciel V2: https://youtu.be/WKIiX6AWkRM?feature=shared
- QHY Pole Master Live: https://youtu.be/IK7yNXvd4tE?feature=shared
Astronomische Beiträge 2025
- Partielle Sonnenfinsternis
- Meine Astro-Fotos 2024
- Auswahl von Astro-Software
- Orientierung am Sternenhimmel
- Supernovae
Astronomische Beiträge 2024
- Beschriftungen (Annotations) mit N.I.N.A.
- Astrofotografie mit der Software StarNet
- Filterschublade für die ZWO ASI294MC Pro
- Der Rotationswinkel bei N.I.N.A.
- Einnorden (Polar Alignment) – Überarbeitet
- Meine Astro-Fotos in 2023
Astronomische Beiträge 2023
- Nachführung: Tracking und Guiding – überarbeitet
- Platesolving mit ASTAP – überarbeitet
- Mein Observatorium
- Software: Tycho Tracker
- Willhelm Olbers
- Das Pariser Observatorium
- Ole Römer und die Lichtgeschwindigkeit
- FITS Header
- Smart Telescopes
- Pulsare
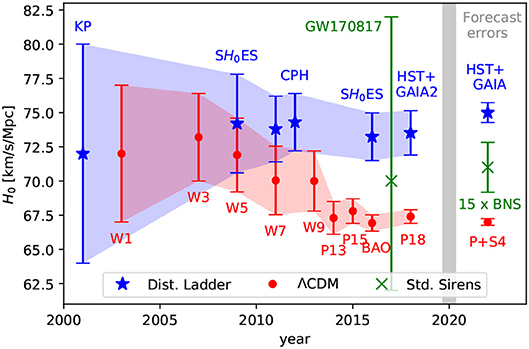
- Die Expansion des Universums
- Flächenhelligkeit
- Aberation
- Claudius Ptolemäus
- Exo-Planeten
- Kugelsternhaufen
- Teleskopsteuerung mit OnStep
- Delta Cepheiden
- Mein Workflow mit N.I.N.A.
- Meine wichtigstes Astro-Zubehör
- Fotografieren mit APT
- Platesolving mit APT
- Meine Astro-Fotos in 2022
Neue astronomische Beiträge 2022
- Fotografieren mit N.I.N.A.
- Astro-Software unter Ubuntu
- Nikolaus Kopernikus
- Heizmanschette gegen Taubeschlag
- Der elektronische Canon-Adapter von AstroMechanics
- Fokussieren mit N.I.N.A.
- Periodic Error Correction
- Harmonic Drive
- Remote Telescopes: iTelescope
- Hertzsprung-Russel-Diagramm
- Hydrostatisches Gleichgewicht
- Entwicklung von Roten Riesen
- ZWO Filter Drawer für Canon (Filterschublade)
- Was ist der StarAid Revolution?
- Der Advanced Sequencer von N.I.N.A.
- Das Three Point Polar Alignment mit N.I.N.A.
- Plate Solving mit N.I.N.A.
- Die Reisemontierung Skywatcher AZ GTi
- Der elektronische Adapter für Canon Objektive von Astromechanics
- Astronomie: Spektralklassen
- Astronomie: Hertzsprung-Russel-Diagramm
- Teleskopsteuerung – Goto-Montierungen
- Teleskopsteuerung über ASCOM mit der SynScan-App
- Verbindung der HEQ5 Pro mit dem Computer
- Teleskopsteuerung mit dem Green Swamp Server
- Der Gegenschein
- Astronomie in Namibia 2022
- Meine Astro-Fotos in 2021
Neue astronomische Beiträge 2021
- Astrofotografie: Tri Narrowband Filter
- Astrofotografie Belichtungszeit hintergrundlimitiert
- Himmelsmechanik Hohmann Transfer Orbit
- Nachführung: Nachführung ohne Autoguiding
- Astrofotografie Bodes Galaxy
- Astrofotografie Pacman Nebel
- Astronomie: Gesellschaft für volkstümliche Astronomie
- Beobachtungsobjekte: Emissionsnebel
- Meine persönliche astronomische Timeline
- Astronomie Liste meiner Fotos
- Astronomie Himmelsmechanik
- Astronomie Die kleine magellansche Wolke mit 47 Tuc
- Plate Solving: AnSvr
- Himmelsmechanik: Lagrange-Punkte
- Astrofoto: IC2944 Running Chicken
- Astrofoto: M8 und M20 Lagoon und Trifid
- Astrofoto: NGC 6334 Katzenpfoten
- Astrofoto: NGC 253 Silverdollar Galaxy
- Astrofoto: Omega Centauri
- Astrofoto: Namibia 47 Tuc
- Teleskope: Backfokus
- Motor-Fokussierer: ZWO EAF
- Astro-Computer: MeLE Quieter 2
- Astrophysik: Metrik und Abstand
- Astrofotografie: Lessons learned
Themenstruktur zur Astronomie
Das Thema Astronomie versuche ich in Themengebiete zu strukturienen:
- Astronomische Geräte
- Teleskope
- Montierungen
- Sucher (Finder Scopes)
- Kameras
- Computer
- Stromversorgung
- Beobachtungsobjekte
- Astrophysik
- Himmelsmechanik
- Radioastronomie
- Astrofotografie
- Polar Alignment
- Fokussierung
- Wie stelle ich mein Bild scharf?
- Bahtinov-Maske
- Hartmann-Maske
- Motor-Fokusser
- Plate Solving
- Nachführung (Tracking, Guiding)
- Astronomische Software
- Planetariumssoftware: Cartes du Ciel
- Planetariumssoftware: Stellarium
- N.I.N.A.
- SiriL
- PHD2 Guiding
- APT
- SharpCap
- ASCOM / EQMOD
- Plate Solving
- Sequence Generator Pro “SGP”
- AutoStakkert
- RegiStax – Wavelets
- Deep Sky Stacker “DSS”
- Fitswork
- StarStaX
- Sonstiges (miscellaneous)
Meine Blog-Artikel zu astronomischen Themen
Es gibt vieles Astronomisches, was man im Internet findet. Ausserdem habe ich als Amateur, der sich ein wenig mit der Astronomie beschäftigt, einige Informationen in meinem Blog zusammengestellt.
Dazu habe ich vieles in einzelnen Artikeln aufgeschrieben:
- Astrofotografie Überblicksartikel
- Astrofotografie: Bildbearbeitung
- Liste meiner astronomischen Geräte
- Digitale Kameras: DSLR
- Astrofotografie mit der Panasonic Lumix FZ-28
- Astrofotografie mit der Sony NEX 5R
- Astrofotografie mit der Canon EOS 600D
- Die Russentonne
- Nachführung mit dem iOptron SkyTracker
- Nachführung mit dem NanoTracker
- Mobile Stromversorgung
- Digitale Kameras: DSLR
- Liste meiner astronomischen Software
- Bildaufnahme mit APT
- Bildaufnahme mit FireCapture
- Bildaufnahme mit SharpCap
- Bildaufnahme mit Backyard EOS
- Bildbearbeitung mit Fitswork
- Bildbearbeitung mit GIMP und PhotoShop
- Bildbearbeitung mit Deep Sky Stacker DSS
- Planetarium-Software Stellarium
- Planetarium-Software Cartes du Ciel
- Planetarium-Software: Guide
- Nachführung mit der Software PHD2 Guiding
- Astronomische Apps für Smartphone und Tablet
- Behandlung von Fotoserien mit XnView und ExifTool
- Picasa mit allen Einstellungen auf neuen PC umziehen
- Orte für astronomische Beobachtungen
- Parkplätze an der A24 für astronomische Beobachtung
- Lichtverschmutzung
- Astrofotografie in Kagga Kamma, Südafrika
- Astrofotografie in Namibia, Südafrika
- Allgemeines zur Astronomie
- Averted Vision – Indirektes Sehen
- Astronomische Entfernungsbestimmung
Vereine und Institutionen für Amateurastronomie
- GvA Gesellschaft für volkstümliche Astronomie: http://www.gva-hamburg.de
- Sternwarte Bergedorf: http://www.sternwarte-hh.de/
- Planetarium Hamburg: http://www.planetarium-hamburg.de
- http://www.havelland-tourismus.de/natur/sternenpark-westhavelland/
Links im Internet zu Astronomischen Themen
Links von Hans:
- Zooniverse: http://www.zooniverse.org
- NED: http://ned.ipac.caltech.edu
- Simbad: http://simbad.u-strasbg.fr/simbad
- Spider: http://spider.seds.org/ngc
- Messier: http://www.messier.seds.org
- VizieR: http://vizier.u-strasbg.fr/
- ESA: http://www.esa.int/Our_Activities/Space_Science
Links von Prof. Dr. Stefan Jordan auf dem ATT 2018
- Gaia ESA: https://www.cosmos.esa.int/web/gaia/home
- Gaia Erklärvideos: https://www.cosmos.esa.int/web/gaia/guide-to-scientists
- Gaia Sky: http://www.zah.uni-heidelberg.de/gaia/outreach/gaiasky
- https://www.youtube.com/playlist?list=PLTUZKJKqW_n-9dlDBQP7CluQw3IVd4dECxxxvvvvv
- Gaia ESA Archive: https://gea.esac.esa.int/archive/
- ARI-Archive: http://gaia.ari.uni-heidelberg.de
Gesammelte Links
- Gesellschaft für volkstümliche Astronomie: http://www.gva-hamburg.de
- Manfred Holls TV-Guide: http://www.manfredholl.de/tvguide.htm
- Forum Astronomie http://forum.astronomie.de
- Astrotreff: http://www.astrotreff.de
- Cloudy Nights: http://www.cloudynights.com
- In der Stadt: http://urbanastronomer.blogspot.de/
- Clear Sky Blog: http://www.clearskyblog.de/
- Erik Wischnewski: http://www.astronomie-buch.de/astronomietelevision.htm
- Astro Bin: http://www.astrobin.com
- Astro Backyard: http://astrobackyard.com/
- 2019 Astronomer’s Guide to the Night Sky: https://hobbyhelp.com/astronomy/planets-visible-tonight/