Gehört zu: Sternentwicklung, Astronomie
Siehe auch: Hertzsprung-Russel-Diagramm, Jeans-Kriterium, Kernfusion, Nova Cygni 1975
Benutzt: SVG-Grafik von pCloud, Fotos von pCloud
Stand: 01. Juli 2025
Supernovae
Warnung / Disclaimer
Diesen Blog-Artikel schreibe ich ausschließlich zu meiner persönlichen Dokumentation; quasi als mein elektronisches persönliches Notizbuch. Wenn es Andere nützlich finden, freue ich mich, übernehme aber keinerlei Garantie für die Richtigkeit bzw. die Fehlerfreiheit meiner Notizen. Insbesondere weise ich darauf hin, dass jeder, der diese meine Notizen nutzt, das auf eigene Gefahr tut. Wenn ich Produkteigenschaften beschreibe, sind dies ausschließlich meine persönlichen Erfahrungen als Laie mit dem einen Gerät, welches ich bekommen habe.
Von “Nova” oder “Supernova” spricht man, wenn plötzlich ein “neuer Stern” sichtbar wird, an einer Stelle wo früher keiner war. Etwas genauer betrachtet ist es ein plötzlicher großer Helligkeitsanstieg.
Historische Beispiele von Supernovae (“SN”) in unserer Galaxis sind:
- SN1054 Bekannteste SN mit dem Crab-Nebel als Überrest
- SN1572 “Tycho Brahe’s Supernova” (Type Ia)
- SN1603 “Keplers Supernova” – die letzte in unserer Galaxie beobachtete SN
Heute wissen wir, dass massereiche Sterne in der Endphase ihrer Entwicklung als Supernova enden können. Ich gehe hier auch ein wenig auf die Sternentwicklung ein, aber der Fokus in diesem Blog-Artikel ist, was am Ende eines “Sternlebens” da evtl. passieren kann.
Klassifikation von Supernovae
In der Astronomie wird viel über Supernovae (SN) gesprochen. Da unterscheidet man verschiedene Typen (Ia, II etc.).
Eine Supernova Typ II entsteht am Ende des Lebenszyklus eines massereichen Sterns. Im Spektrum einer Supernova Typ II sind alle möglichen Elemente zu sehen besonders die Linien des Wasserstoffs.
Klassifizierungen von Supernovae wurden historisch auf rein phänomenologischer Basis (im Wesentlichen dem Spektrum) gemacht. Man wusste also noch nicht, was da physikalisch tatsächlich passiert.
Rudolph Minkowski unterschied 1941 zumindest zwei verschiedene Typen, eine die Wasserstoff im Spektrum zeigte: Typ II und eine, die keinen Wassserstoff im Spektrum zeigte: Typ I.
Neben dem Spektrum konnte man auch die Lichtkurve beobachten und aus dem Verlauf Untertypen definieren.
Abbildung 1: Klassifikation von Supernovae (pCloud: Supernova.svg)
Quelle: https://astronomy.swin.edu.au/cosmos/*/Supernova+Classification
Sternentwicklung
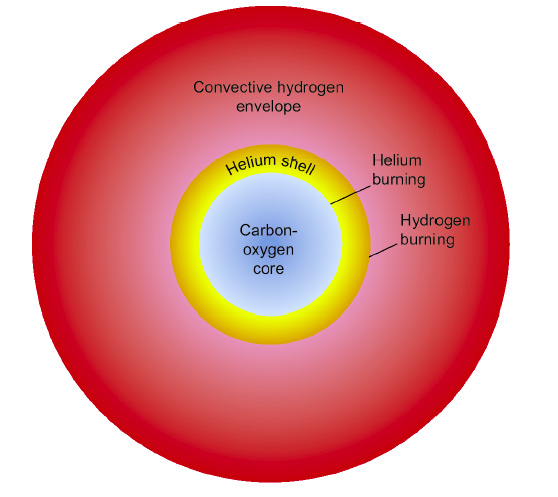
Ein Stern entsteht, wenn sich eine Gaswolke (ionisiertes Gas) unter dem Druck der eigenen Gravitation zusammen zieht (vgl. Jeans-Kriterium) und dann im Inneren die Temperatur ansteigt bis bei ca. 10-15 Mio. Kelvin die Fusion von Wasserstoff zu Helium beginnt. Dadurch entsteht ein Gegendruck zum Gravitationsdruck und es bildet sich ein Gleichgewicht aus. Solche Sterne bilden im Hertzsprung-Russel-Diagramm die sog. Hauptreihe.
Wenn der Kernbrennstoff im Inneren (da wo die Temperatur ausreichte) verbraucht ist, endet die Kernfusion es gibt keinen Gegendruck mehr zum nach innen gerichteten Gravitationsdruck. Der Stern kollabiert, wobei die Temperatur im Inneren weiter steigt. Wenn die Temperatur hoch genug steigt, können weitere Stufen der Kernfusion beginnen. Der Stern verlässt die Hauptreihe im HRD und entwickelt sich zum Roten Riesen.
Die Kernfusion im Inneren eines Stern läuft im Prinzip in Stufen ab:
- Fusion Wasserstoff zu Helium ab 15 Mio Kelvin
- Fusion Helium zu Kohlenstoff ab 100 Mio Kelvin
- Fusion Kohlenstoff zu Sauerstoff ab 500 Mio Kelvin
- Fusion Sauerstoff zu Silizium ab 2100 Mio Kelvin
- Fusion Silizium zu Eisen ab 3400 Mio Kelvin
Eine Stufe der Kernfusion endet, wenn der Kernbrennstoff dieser Stufe (in der heißen Fusionszone des Sterns) verbraucht ist. Es beginnt dann eine Kontraktion mit Temperaturerhöhung. Ob die für weitere Fusionsprozesse erforderliche Temperatur erreicht werden kann, hängt wesentlich von der Masse des Stern ab.
Eine Supernova Typ Ia kann aus einem engen Doppelsternsystem entstehen, wenn einer der beiden Sterne ein Weißer Zwerg ist und dieser Masse (Wasserstoff) vom größeren Begleiter aufnehmen sollte und zwar mehr als die kritische Chandrasekhar-Grenze erlaubt. Der Kohlenstoff im Inneren zündet schlagartig, was zu einer thermonuklearen Explosion führt. Der Weiße Zwerg explodiert in einer Supernova.
Da der Weiße Zwerg keine Wasserstoffhülle hatte, gibt es keine sichtbare Wasserstofflinie im Spektrum.
Der Weiße Zwerg wird bei der Explosion vollständig zerstört; es bleibt kein kompakter Überrest zurück.
In Abhängigkeit von der Anfangsmasse eines Sterns, werden typische Entwicklungs-Stadien durchlaufen. Wenn die Kernfusion ganz aufgehört hat, ist das Ende des Sterns erreicht. Durch den dann einsetzenden Gravitationskollaps können verschiedene Endprodukte entstehen.
- > 8 Sonnenmassen: Hauptreihenstern, Roter Riese mit Kernfusion bis nur noch Fe übrig ist, danach Kollaps als Supernova Typ II (Spektrum mit Wasserstoff u.a.), der Rest wird ein Neutronenstern evtl. ein Schwarzes Loch
- Neutronenstern, wenn Restmasse < 3,2 Sonnenmassen
- Schwarzes Loch, wenn Restmasse >= 3,2 Sonnenmassen
- < 8 Sonnenmassen: Hauptreihenstern, Roter Riese mit Kernfusion bis nur noch Kohlenstoff und Sauerstoff übrig sind, Kollaps zu einem Weissen Zwerg mit Planetarischem Nebel
- Weißer Zwerg, mit Restmasse < 1,44 Sonnenmassen (Chandrasekhar-Grenze)
Link: https://www.studysmarter.de/schule/physik/astronomie/sternentwicklung/
Standardkerzen
Eine Supernova vom Type Ia wird auch als “Standardkerze” bezeichnet, da die Sternmasse klar definiert ist (Chandrasekhar-Grenze) und die Helligkeitskurve so einer thermonuklearen Explosion gut modelliert werden kann. Da die Lichtintensität mit dem Quadrat der Entfernung abnimmt, kann man solche Standardkerzen gut zur Entfernungsbestimmung verwenden.
Aber was ist im Gegensatz zu einer Supernova denn eigentlich eine Nova?
Eine Nova tritt wie eine Supernova Typ Ia in einem Doppelsternsystem mit einem Weißen Zwerg auf, der Materie von seinem Begleitstern absaugt. Anders als bei der Supernova Ia zündet hier nur die aufgesammelte Wasserstoffschicht auf der Oberfläche des Weißen Zwergs in einer thermonuklearen Reaktion. Der Weiße Zwerg selbst bleibt dabei erhalten und kann diesen Prozess mehrfach durchlaufen.
Ich selbst konnte im Jahre 1975 die Nova Cygni beobachten.
Über “normale” (also nicht “Super”) Novae habe ich gehört, dass es da zwei Typen gibt:
- “CV” = Cataclysmic Variable Stars (Kataklysmische Doppelsterne, mit Massentransfer von einem Stern zum anderen)
- “CE” = Common Envelope Binaries (ein enges Doppelsternsystem, auch symbiotisch genannt, ein Stern befindet sich in der Hülle des anderen)
Im Prinzip kann man Novae als “Veränderliche Sterne” verstehen.
Mein Foto der Supernova 2023ixf
Anfang Juni 2023 (05.06.2023) konnte ich von meiner Terrasse in Hamburg-Eimsbüttel (Bortle 7) mit meinem ED80/600 auf HEQ5 Pro, ASI294MC Pro, Gain 200, -10°C, 86×60 sec die Supernova in M101 aufnehmen. Diese SN war vom Typ II – also Kernkollaps.
Abbildung 2: M101 mit Supernova (pCloud: 20230605_M101b.jpg)

Abbildung 3: M101 ohne Supernova (pCloud: 20240430_Bundesstrasse_M101b.jpg)

Es ist also möglich, ein schwaches, flächiges Objekt wie M101 am lichtverschmutzten Hamburger Himmel (Bortle 7) zu fotografieren.
Vergleiche: