Mathematik

Mathematik: Matrizenrechnung – Vektorraum

dkracht

Gehört zu: Mathematik
Siehe auch: Lineare Algebra
Benutzt: WordPress-Plugin Latex

Matrizen als Lineare Abbildungen

Jede (nxm)-Matrix ist per Matrixmultipikation eine lineare Abbildung von \(\mathbb{R}^m\) nach \(\mathbb{R}^n\)

Quelle: https://www.mathematik.de/algebra/74-erste-hilfe/matrizen/2429-lineare-abbildungen

Lineare Abbildungen als Matrizen

Eine Lineare Abbildung kann eindeutig beschrieben werden durch die Werte auf die die Basis-Vektoren einer Basis abgebildet (transformiert) werden.

Beispielsweise heisst das im Vektorraum \(\mathbb{R}^2\) mit dem kanonischen Koordinatensystem und den Basisvektoren \( \hat{i} \) und \( \hat{j}  \) folgendes:

Wenn wir einen Vektor \( \vec{v} = \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x \hat{i} + y\hat{j} \) betrachten, so wirkt eine Lineare Transformation L wie folgt:

\( L(\vec{v}) = x L(\hat{i}) + y L(\hat{j} )  \)

Wenn wir also die transformierten Basisvektoren \( L(\hat{i}) \) und \( L(\hat{j}) \)  kennen, ist damit die Lineare Transformation L vollständig festgelegt.

Diese transformierten Basis-Vektoren können im verwendeten Koordinatensystem als Matrix schreiben.

Wenn bei unserer Linearen Transformation beispielsweise \( L(\hat{i}) = \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] \)   und \( L(\hat{j}) = \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] \)  wäre, bekämen wir eine Matrix:

\( \left[ L(\hat{i}) | L(\hat{j}) \right] = \left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right] \)

Wir “konkatenieren” also die transformierten Basis-Vektoren vertikal als Spalten.
Die Lineare Transformation kann im benutzten Koordinatensystem als Matrixmultiplikation aufgefasst werden:

\(\left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right]  \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x  \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] + y  \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] = \left[ \begin{array}{c} 3x+2y \\\ -2x+1y  \end{array} \right] \\\)

Völlig analog werden auch Lineare Transformationen in drei oder mehr (endlichen) Dimensionen behandelt.

Eigenschaften von Matrizen

Viele der Überlegungen, die wir mit Linearen Abblidungen vorgenommen haben, können wir also gleichermaßen auf Matrizen übertragen.

Sei also A die  (nxn)-Matrix zur Linearen Abblidung L von einem Vektorraum V in einen Vektorraum W (beide über dem gleichen Körper K)

\(  L: V  \to W \\\)

So haben wir beispielsweise zu L im Falle dim(V) = dim(W) = 3  eine (3×3)-Matrix A:

\(\Large A =  \left( \begin{array}{rrr} a_{11} & a_{12} & a_{13}\\  a_{21} & a_{22} & a_{23} \\  a_{31} & a_{32} & a_{33} \end{array} \right)  \\\)

Das Bild einer Matrix

Das Bild (engl. image) der Matrix A ist die Menge:

\(  im(A) =\{ y \in W \,| \,\exists x \in V \, : \, Ax = y \} \\\)

im(A) ist wiederum ein Untervektorraum von W.

Der Rang einer Matrix

Der Rang einer Matrix ist die Anzahl linear unabhängiger Zeilen- oder Spaltenvektoren der Matrix.
Bei einer quadratischen (n×n)-Matrix bedeutet dies, er ist höchstens n.

Rang(A) = dim(im(A))

Der Kern einer Matrix

Der Kern der Matrix A ist die Menge der Vektoren, die auf den Null-Vektor abgebildet werden:

\(  ker(A) =\{ x \in V \,|  \, Ax = 0 \} \\\)

ker(A) ist wiederum ein Untervektorraum von V.

Mit anderen Worten: Der Kern von A ist also die Lösungsmenge des Linearen Gleichungssystems Ax=0

Die Determinante einer Matrix

Bei einer quadratischen (n×n)-Matrix ist die Determinante genau dann 0 ist, wenn ihr Rang der Matrix kleiner n ist.

Computer: Mathematik – Algebren

dkracht

Gehört zu: Mathematik
Siehe auch: Vektorräume, Quantenfeldtheorie
Benutzt:  WordPress Plugin for Latex

Stand: 23.2.2022

Algebren

Ein Vektorraum V über einem Körper K zusammen mit einer bilinearen Abbildung:

\(  V \times V \to V \)

wird eine Algebra genannt.

Die bilineare Abbildung wird “Produkt” (auch: Multiplikation) genannt und auch so wie ein Produkt hingeschrieben; also:  a · b  oder einfach ab. In dieser Schreibweise bedeutet die Bilinearität einfach folgendes:

\(   (x + y) \cdot z = x \cdot z + y \cdot z  \\ \)
\(   x \cdot (y + z)  = x \cdot y + x \cdot z  \\ \)
\( a (x \cdot y) = (ax) \cdot y = x \cdot (ay) \\ \)

Dabei sind x,  y und z Vektoren aus V und a ein Skalar aus K.

Das “besondere” an Algebren ist die “Multiplikation”. Deswegen unterscheidet man  Algebren auch nach den Eigenschaften dieser Multiplikation:

Kommutative – nicht-kommutative Algebren: Ist immer \( a \cdot b  =  b \cdot a \) oder nicht?

Assoziative – nicht-assoziative Algebren: Ist immer \( a \cdot (b \cdot c) = (a \cdot b) \cdot c \) oder nicht?

Beispiele für Algebren:

Die n × n Matrizen über einem Körper mit der gewöhnlichen Matrizenmultiplikation als “Multiplikation” bilden eine assoziative Algebra.

Ein Vektorraum V mit dem Kreuzprodukt als Multipikation bildet eine nicht-assoziative Algebra.

Lie-Algebren

Bestimmte Algebren heissen “Lie-Algebren” (nach Sophus Lie 1842-1899), dort wird das Produkt meist als [x,y] geschrieben und “Lie-Klammer” genannt.
Eine Lie-Algebra ist eine Algebra, in der die beiden folgenden Bedingungen gelten:

  • [x,x] = 0
  • [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 (“Jacobi-Identität”)

Beispiel für eine Lie-Algebra:

Ein Vektorraum V mit dem Kreuzprodukt als Multipikation bildet eine Lie-Algebra.

Kommutator

Im allgemeinen definiert man als Kommutator in Ringen und assoziativen Algebren: [a,b] = ab – ba
So ein Kommutator kann in bestimmten Algebren als Lie-Klammer fungieren. Beispielsweise kann man aus der oben erwähnten Algebra der n x n Matrizen mit der gewöhnlichen Matrixmultiplikation eine Lie-Algebra machen, indem man den Kommutator der Matrixmultiplikation als Lie-Klammer nimmt.

Lie-Algebren in der Physik

Solche Lie-Algebren werden in der Quantenfeldtheorie praktisch gebraucht.

Mathematik: Metrik, Abstand und Geometrie

dkracht

Gehört zu: Mathematik
Siehe auch: Krümmung, Vektorraum, Wirkung, Schwarzschild-Metrik, Metrik-Tensor
Benutzt: WordPress-Plugin Latex, GeoGebra Grafikrechner

Metrik, Abstand und Geometrie

Auf einer Menge M kann man eine Metrik definieren; dadurch dass man je zwei Punkten einen Abstand (relle Zahl >= Null) zuordnet.

d: M x M -> R

So eine Abstandsfunktion muss drei Axiome erfüllen, um Metrik genannt werden zu dürfen.

Oft ist den Beispielen die Menge M ein Vektorraum z.B. R2 oder R3.

Mit Hilfe einer solchen Metrik kann man eine ganze “Geometrie” definieren, also ein Regelwerk für Punkte, Geraden, Winkel, Dreiecke etc. Klassisch ist die Geometrie nach Euklid; andere Geometrien bezeichnet man als “Nicht-Euklidische Geometrie”…

Euklidische Geometrie

In der sog. Euklidischen Geometrie wird der Abstand im zweier Punkte im Raum (also die Metrik) durch den Satz des Pythagoras definiert.

Zur Berechnung des Abstands zweier Punkte verwenden wir ein Koordinatensystem z.B.  im R3 eine x-Achse, eine y-Achse und eine z-Achse:

\( d((x_a,y_a,z_a),(x_b,y_b,z_b)) = \sqrt{(x_b-x_a)^2 + (y_b-y_a)^2 – (z_b-z_a)^2} \\\  \)

Dieser Abstand ist auch die Länge der geraden Strecke zwischen den Punkten a und b.

Im allgemeinen Fall nehmen wir eine parametrisierte Kurve α: [a,b] -> Rn  und definieren als Länge L der Kurve α:

\( L_\alpha(a,b) = \int_a^b ||\alpha^\prime(t)|| dt \\\ \)

Wir können zeigen, dass diese Längendefinition für Kurven mit der Metrik für Punktabstäde im Euklidischen Raum überein stimmt (ohne Beschänkung der Allgemeinheit: t ∈ [0,1]):

\( \alpha(t) = \left( \begin{array}{c} x_1 + (x_2-x_1) \cdot t \\\ y_1 + (y_2-y_1)\cdot t  \\\  z_1 + (z_2-z_1)\cdot t\end{array}\right)  \\\  \)

Die erste Ableitung ist:

\( \alpha^\prime(t) = \left( \begin{array}{c} (x_2-x_1)  \\\ (y_2-y_1) \\\  (z_2-z_1) \end{array}\right)  \\\  \)

Die Norm der Ableitung ist dann:

\( || \alpha^\prime(t) || = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2} \\\ \)

Wenn wir das in die obige Längendefinition einsetzen erhalten wir:

\( L_\alpha(a,b) = \int_a^b ||\alpha^\prime(t)|| dt = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}  \int_0^1 dt  = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}  \\\ \)

Die Länge einer geraden Strecke ist also auch mit der allgemeinen Integral-Formel genauso wie nach Pythagoras oben.

Das Linienelement

Gerne verwendet man auch ein sog. Linienelement um eine Metrik zu definieren. Für die Euklidische Metrik im dreidimensionalen Raum mit einem Chartesischen Koordinatensystem (x,y,z) haben wir das Linienelement:

\( ds^2 = dx^2 + dy^2 + dz^2 \\\  \)

Was ergibt:

\( ds = \sqrt{dx^2 + dy^2 + dz^2} \\\  \)

Was für eine parametrisierte Kurve s: [a,b] -> R3 bedeutet:

\( \Large \frac{ds}{dt} = \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2 + (\frac{dz}{dt})^2} \\\  \)

Was als Kurvenlänge von t=a bis t=b ergibt:

\( \Large L(a,b) = \int_a^b \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2 + (\frac{dz}{dt})^2} dt \\\  \)

Wenn man nun bedenkt dass:

\( s^\prime = \frac{ds}{dt} = \left( \begin{array}{c} \frac{dx}{dt}  \\\ \frac{dy}{dt} \\\  \frac{dz}{dt} \end{array}\right) \\\  \)

ist, ergibt sich die Norm zu:

\( || s^\prime || = \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2 + (\frac{dz}{dt})^2} \\\ \)

Eingesetzt ergibt das:

\( \Large L(a,b) = \int_a^b || s^\prime || dt \\\ \)

was genau der ersten Definition (oben) entspricht.

Man kann auch zeigen, dass die so definierte Länge einer parametrisierten Kurve bei Umparametrisierungen der Kurve gleich bleibt.

Der Metrik-Tensor

Im allgemeinen Fall drücken wir das Linienelement in einem Koordinatensystem mithilfe des “Metrik-Tensors” \(g_{\mu\nu}\) aus:

\( ds^2 = g_{\mu\nu} dx^\mu dx^\nu \\\ \)

Im Falle der Euklidischen Geometrie im R3 ist im Chartesischen Koordinatensystem der metrische Tensor:

\( g =  \left[ \begin{array}{rrr} 1 & 0 & 0\\  0 & 1 & 0 \\  0 & 0 & 1 \end{array} \right]  \\\)

Ein “Tensor” in diesem Sinne ist nichts anderes als eine (n x n)-Matrix für die man noch einige zusätzliche Regeln hat.

Weiterführende Anmerkungen

Nach der Allgemeinen Relativitätstheorie ART von Einstein, verändert die Anwesenheit von Materie den Raum, was auch “Gravitation” genannt wird.

Wir können das als eine Nicht-Euklidische Metrik verstehen, für die beispielsweise Karl Schwarzschild schon 1916 im vereinfachten Fall einer Kugelmasse (Schwarzes Loch) eine Formel gefunden hat.

Zu Veranschaulichung so einer Nicht-Euklidischen Metrik wird häufig von einer “Krümmung” der Raumzeit gesprochen. Diese “Krümmung” ist aber eigentlich nur eine andere Metrik, trotzdem stellt man sich die Abweichung von der herkömmlichen Euklidischen Metrik gern als “Krümmung” vor,

Da diese “Krümmung” (also Abweichung von der Euklidischen Metrik) aber nicht in eine weitere Dimension, sondern “in sich” d.h. als Stauchung bzw. Streckung erfolgt, würde ich gerne eine solche Abweichung durch ein Verbiegen des Koordinatengitters veranschaulichen. Also durch den optischen Vergleich der Koordinatengitter zweier Metriken.

===> Das Gitter, was ich hier meine, ist ein durch gleiche Abstände in der jeweiligen Metrik gegebenes Gitter – ist also eigentlich kein schlichtes Koordinatengitter, sondern ein Metrik-Gitter…

GeoGebra Gitternetz

Schwarzschild-Metrik

Ich habe zum Thema Schwarzschild-Metrik einen eigenen Artikel geschrieben.

 

 

Physik: Krümmung der Raumzeit

dkracht

Gehört zu: Physik
Siehe auch: Relativitätstheorie, Vektorraum, Gravitation, Schwarze Löcher, Metrik

Krümmung der Raumzeit

Die Allgemeine Relativitätstheorie (ART) basiert auf dem Postulat der Äquivalenz von Gravitation und Beschleunigung.

Aus diesem Äquivalenzprinzip ergibt sich die Lichtablenkung in Gravitationsfeldern.

Wenn man trotzdem davon ausgehen möchte, dass das Licht immer den kürzesten Weg nimmt, muss die Gravitation den Raum (besser die Raumzeit) entsprechend krümmen, sodass eine Metrik entsteht bei der der kürzeste Weg zwischen zwei Punkten nicht unbedingt die Euklidische gerade Linie ist.

Wir wollen hier zunächsteinmal den Begriff der “Krümmung” ganz allgemein diskutieren.

Umgangssprachlich denkt man bei “Krümmung”, dass sich etwas in eine zusätzliche Dimension krümmt (s.u. die vielen Beispiele). Bei der von Einstein postulierten Krümmung der vierdimensionalen Raumzeit wird aber für diese Krümmung keine 5. Dimension gebraucht. Die vierdimensionale Raumzeit ist nach Einstein  “in sich” gekrümmt; d.h. wir haben einen anderen Abstandsbegriff (eine andere Metrik, ein anderes Linienelement).

Krümmung bei Euklidischer Metrik

Unter der Krümmung eines geometrischen Objekts versteht man die Abweichung von einem geraden Verlauf; dazu bedarf es (mindestens) einer weiteren Dimension in die die Krümmung verläuft oder der Begriff “gerade” muss umdefiniert werden. Eine Kurve verläuft “gerade” wenn beim Durchlaufen mit konstanter Geschwindigkeit, keine Beschleunigungen “seitwärts”, sonder höchstens in der Normalen auftreten.

Wir betrachten eine Gerade. Solange sie wirklich geradeaus verläuft ist sie nicht gekrümmt. Wenn sie eine Kurve nach links (oder rechts) macht, haben wir eine Krümmung – und wir brauchen dafür (mindestens) eine zweite Dimension. Die Stärke der Krümmung kann mehr oder weniger sanft oder kräftiger sein. Wir messen die Stärke der Krümmung an einer Stelle durch einen sog. Krümmungskreis. Das ist ein Kreis, der sich in dem betrachteten Punkt am besten an die Kurve anschmiegt. Ein großer Krümmungskreis bedeutet eine kleine Krümmung ein kleiner Krümmungskreis ein starke Krümmung. Der Kehrwert des Radius ist das Maß für die Krümmungsstärke.

Die andere Frage ist, welche geometrischen Objekte sind es, die da “gekrümmt” werden?  Im einfachsten Fall ist es eine eindimensionale Linie in einer zweidimensionalen Ebene; also z.B. ein Funktionsgraph oder eine sog. Kurve. Kurven sind in diesem Zusammenhang sehr interessant als Teilmenge eines Vektorraums, die durch eine Abbildung von einem reellen Intervall in den Vektorraum  als sog. “parametrisierte” Kurve dargestellt werden kann. Das “Umparametrisieren” ist dann eine Äquivalenzrelation zwischen parametrisierten Kurven. Eine “Kurve” kann dann als Äquivalenzklasse solcher parametrisierten Kurven verstanden werden. Als Repräsentant einer Äquivalenzklasse nimmt man dann gerne eine nach Bogenlänge parametrisierte Kurve.

Wenn wir uns mit Kurven beschäftigen und speziell dann mit der Länge einer Kurve oder der Krümmung von Kurven, haben wir es mit Differentialgeometrie zu tun.
Dazu gibt es eine Reihe von sehr schönen Youtube-Videos:

Schritt 1: Krümmung einer Linie in der Ebene

Wenn das betrachtete Objekt ein Funktionsgraph von beispielsweise y = f(x) in der Ebene ist, können wir die Krümmung leicht berechnen:

Für eine zweimal differenzierbare Funktion  y = f(x) ergibt sich der Krümmungsradius an einem Punkt x zu:

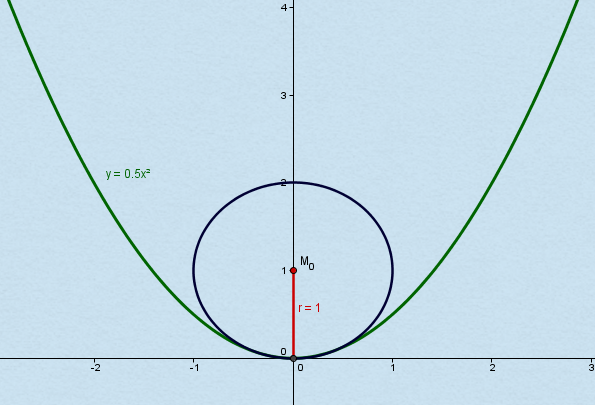
\( \Large  r(x) = \left\vert \frac{(1+(f^\prime(x))^2)^\frac{3}{2}}{f^{\prime\prime}(x)} \right\vert  \)

Als Beispiel nehmen wir mal eine Parabel f(x) = 0,5 * x2
Dazu haben wir die Ableitungen:
f‘(x) = x
f“(x) = 1
Der Krümmungsradius beispielsweise am Punkt x0 = 0 beträgt dann laut obiger Formel:

\( \Large r(x_0) = \frac{(1+{x_0}^2)^{\frac{3}{2}}}{1} = 1 \\\ \)

Und zur Probe nehmen wir noch x=1:

\( \Large r(1) = \frac{(1+1^2)^{\frac{3}{2}}}{1} = 2^\frac{3}{2} = 2 \sqrt{2} \)

Dieses Beispiel habe ich entnommen aus https://www.ingenieurkurse.de/hoehere-mathematik-analysis-gewoehnliche-differentialgleichungen/kurveneigenschaften-im-ebenen-raum/kruemmung/kruemmungsradius.html
Es wird grafisch veranschaulicht durch:

Schritt 2: Krümmung einer Kurve in der Ebene

Wenn das betrachtete Objekt eine “richtige” Kurve in der Ebene ist, wird die Krümmung anders berechnet.

Als “richtige” Kurve (in der Ebene) betrachten wir von der obigen Parabel das Kurvenstück von x=-1 bis x=1. Als Parametrisierte Kurve, wobei der Parameter t auch von -1 bis 1 laufen möge, (was wir uns z.B. als Zeit vorstellen könnten) sieht das dann so aus:

\( \Large \alpha(t) = \left( \begin{array}{c} t \\\ \frac{1}{2}t^2  \end{array}\right)  \\\  \)

Um die Krümmung zu brechnen ermitteln wir zuerst:

\( \Large \alpha^\prime(t) = \left( \begin{array}{c} 1 \\\ t  \end{array}\right)  \)

womit dann:

\( \Large ||\alpha^\prime(t)||^2 =  1 +  t^2   \\\  \)

und mit:

\( \Large \alpha^{\prime\prime}(t) = \left( \begin{array}{c}  0 \\\ 1  \end{array}\right)  \)

ergibt sich:

\( \Large det(\alpha^\prime(t), \alpha^{\prime\prime}(t)) = 1  \\\ \)

und damit ergibt sich dann die Krümmung zu:

\( \Large \kappa_\alpha(t) = \frac{1}{(1 + t^2 )^\frac{3}{2}}  \)

Bei t=0 ist dann die Krümmung:

\( \Large \kappa_\alpha(0) = 1 \\\  \)

und zur Probe nehmen wir noch t=1:

\( \Large \kappa_\alpha(1) = \frac{1}{2 \sqrt{2}} \\\ \)

Weil t=x ist, stimmt das mit den Berechnungen des Krümmungsradius (s.o. Schritt 1) exakt überein.

Schritt 3: Krümmung einer Fläche im Raum

Analog können wir uns gekrümmte Flächen im Raum vorstellen. Hier kann allerdings der Krümmungsradius in unterschiedlichen Richtungen unterschiedlich sein. Inetwa so die wir das von einem Gradienten kennen.

Auch in diesem Fall stellen wir uns das ganz klassisch geometrisch vor als Krümmung in eine weitere Dimension.

Krümmung per Nicht-Euklidischer Metrik

In der Allgemenen Relativitätstheorie spricht man auch von “Krümmung” z.B. Krümmung des Raumes oder Krümmung der Raumzeit.

Hier basiert die “Krümmung” nicht auf einer zusätzlichen Dimension, sondern auf einer speziellen Metrik in ein und demselben Raum. Unter “Metrik” versteht man ja eine Vorschrift, die zwei Punkten in dem betreffenden Raum einen Abstand zuordnet.  So eine Metrik definiert dann auch automatische die Längen von Linien…

Geodätische Linie

Die Linie, die die kürzeste Verbindung zwischen zwei Punkten bildet, nennt man Geodät oder auch Geodätische LInie. Auf der Erdoberfläche kennen wir das z.B. bei der Seefahrt oder Luftfahrt wenn wir beispielsweise die Flugroute von London nach Los Angeles betrachten:

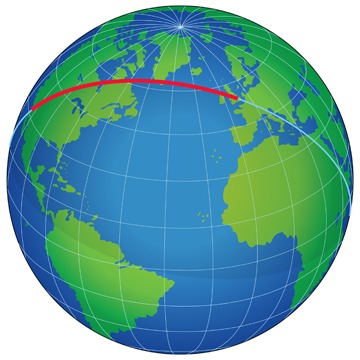
Geodätische LInie Moskau - Los Angeles

Das Licht läuft immer auf einer Geodäte, nimmt also die kürzeste Verbindung. Das kann “gekrümmt” aussehen…

Krümmung ohne zusätzliche Dimension

Für eine solche Krümmung benötigen wir aber nicht zwingend eine zusätzliche Dimension. Die Krümmung kann auch “in sich” durch andere Abstandsgesetze (= Metriken) bewirkt werden.
Siehe Schwarzschild-Metrik

 

Mathematik: Data Science

dkracht

Gehört zu: Mathematik
Siehe auch: Python

Ein neues Buzzword: Data Science

Öfters habe ich schon Vorlesungen auf dem Youtube-Kanal von Prof. Dr. Weitz von der Hamburger Hochschule für Angewandte Wissenschaften (“HAW” – früher: Fachhochschule Berliner Tor) gehört.

Er arbeitet da mit Computer-Software wie:

  • MATLAB
  • Mathematica, was sehr teuer ist. Kann CDF-Dateien erzeugen, die mit einem CDF Player abgespielt werden können
  • jupyter: Link https://jupyter.org/
  • SymPy: Link https://www.sympy.org/en/index.html
  • GeoGebra Link: https://www.geogebra.org/?lang=de
  • WolframAlpha Link: https://www.wolframalpha.com/
  • p5.js Link: https://editor.p5js.org/
  • Anaconda (zum Installieren von Paketen etc.) Link: https://www.anaconda.com/individual-tutorial?source=win_installer

und anderen.

Herr Weitz unterscheidet sog. Computer Algebra Systeme (abgekürzt CAS) von Numerischen Systemen…

Als Programmiersprache kommt man wohl an JavaScript nicht vorbei, das sich in den letzten Jahren enorm weiterentwickelt hat: z.B. https://eloquentjavascript.net/Eloquent_JavaScript.pdf

 

 

Mathematik: Komplexe Zahlen

dkracht

Gehört zu: Mathematik
Siehe auch: Quantenmechanik, Von Pytharoras bis Einstein, Schrödinger-Gleichung
Benutzt: WordPress-Plugin Latex

Stand: 29.7.2022

Die komplexen Zahlen

Ausgangspunkt ist die berühmte imaginäre Einheit: i2 = -1

Eine komplexe Zahl schreibt man gerne als Realteil und Imaginärteil:

z = x + i*y      x = Re(z)   und   y = Im(z)

Wobei x und y reelle Zahlen sind.

Mit den Komplexen Zahlen kann man auch die vier Grundrechnungsarten, so wie wir sie von den “normalen” d.h. reellen Zahlen her kennen, ausführen – Die komplexen Zahlen bilden, mathematisch gesagt, einen “Körper”.

Zu jeder Komplexen Zahl gibt es die “komplex konjugierte“, die mit gern mit einem Sternchen als Superskript schreibt:

zur komplexen Zahl: z = x + i*y
ist die konjugierte:   z* = x – i*y

Manchmal schreibt man die komplex konjugierte auch mit einem Strich über der Zahl. Also:

\( \overline{x + y \cdot i} = x – y \cdot i \)

 

Jede Komplexe Zahl hat auch einen “Betrag” (kann man sich als Länge vorstellen):

|z|2 = x2 + y2

Interessanterweise ist der Betrag (Länge) einer Komplexen Zahl auch:

|z|2 = z z*

Darstellung der komplexen Zahlen mit kartesischen Koordinaten

Die Reellen Zahlen konnte ich mir ja durch die sog. Zahlengerade gut veranschaulichen. Die Komplexen Zahlen würde ich mir dann durch die Punkte in einer Ebene veranschaulichen.

Polar-Darstellung der komplexen Zahlen

Wenn komplex Zahlen einfach als Punkte in der Ebene verstanden werden können, kann ich sie anstelle von kartesischen Koordinaten, alternativ auch in durch sog. Polarkoordinaten darstellen; d.h. durch die Entfernung vom Nullpunkt r und den Winkel mit der reellen Achse φ.

Für eine Komplexe Zahl z = x + i*y  gilt:

r² = x² + y²

tan φ = x/y

\(\displaystyle \tan{ \phi} = \frac{x}{y} \)

Exponential-Darstellung der komplexen Zahlen

Die Eulerschen Formel ist:

\(\Large  e^{i  \cdot \phi} = \cos \phi+i \cdot \sin \phi \\\)

Damit können wir jede komplexe Zahl auch in sog. Exponential-Darstellung schreiben:

\(\Large z ={r} \cdot e^{i  \cdot \phi} \\ \)

Das funktioniert so gut, weil die Multiplikation von Potenzen der Addition der Exponenten entspricht und das mit den Summenformeln der Trigonometrie übereinstimmt.

Den Winkel φ nennt man auch “die Phase”.

Wenn die Komplexen Zahlen den Betrag 1 haben, also auf dem Einheitskreis liegen, hat man:

\( e^{i \phi} = cos{\phi} + i sin{\phi} \)

und man spricht von einer “reinen Phase”.

In der Quantenmechanik wird diese Exponentialdarstellung gerne benutzt, u.a. weil man damit die Multiplikation komplexer Zahlen sehr anschaulich darstellen kann:

\(\Large z_1 \cdot z_2 = {r_1 \cdot r_2} \cdot e^{i  \cdot (\phi_1 + \phi_2)} \\ \)

Sie auch Youtube-Video:

Die Eulersche Zahl

Definition der Eulerschen Zahl

Die Zahl e wurde von Leonhard Euler (1707-1783) als Grenzwert der folgenden unendlichen Reihe definiert:

\(\displaystyle e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} +  \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} + …   \)

Oder:

\(\displaystyle e = \sum_{n=0}^{\infty} \frac{1}{n!} \)

Die Exponentialfunktion

Potenzen zur Basis e bilden die Exponentialfunktion, auch e-Funktion genannt:

f(x) = ex

Die Ableitung (Differentialquotient) der e-Funktion ist wiederum die e-Funktion:

f'(x) = ex

Damit ergibt sich als Taylorsche Reihenentwicklung um den Entwicklungspunkt x0 = 0

\(\displaystyle f(x) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}  + …  + \frac{x^n}{n!} + …   \)

Allgemein wäre die Taylor-Reihe ja:

\( \displaystyle T_\infty(x;x_0) = \sum_{k=0}^{\infty} \frac{f^(k)(x_0)}{k!} (x-x_0)^k \)

Da der Funktionswert und alle Ableitungen der e-Funktion an der Stelle x0 = 0 sämtlich 1 sind, vereinfacht sich die Darstellung wie oben gezeigt.

Mathematik: Was sind Tensoren?

dkracht

Gehört zu: Mathematik
Siehe auch: Quantenmechanik,  Vektorräume, Lineare Algebra, Koordinatensysteme, Metrik-Tensor, Kontravariante Ableitung
Benutzt: WordPress-Plugin Latex

Stand: 26.10.2021

Was sind Tensoren?

Eine der Voraussetzungen zum Verständnis vieler Dinge (z.B. in der Allgemeinen Relativitätstheorie und der Quantenmechanik) sind sog. Tensoren.

Der Begriff “Tensor” wurde im 19. Jahrhundert relativ unsystematisch bei verschiedenen physikalischen Berechnungen eingeführt.

Darüber gibt es schöne Youtube-Videos von “eigenchris”:  https://youtu.be/sdCmW5N1LW4

Als Vorbereitung dazu habe ich zuerst mal etwas zu Vektorräumen zusammengestellt.

Auffrischung

Wir hatten ja im Artikel über Vektorräume schon gesehen, dass Vektoren Objekte sind, die unabhängig von Koordinatensystemen exsistieren und auch gegenüber einem Wechsel von Koordinatensystemen “invariant” sind. Nur die Komponenten bzw. Koordinaten der Vektoren verändern sich dann, nicht aber die Vektoren selber.

Invarianz bedeutet allgemein gesagt, dass ein und dasselbe Objekt verschieden beschrieben (“repräsentiert”) werden kann von verschiedenen Standpunkten (Koordinatensystemen) aus.

Unsere Vektorkomponenten beruhen immer auf einer Menge von sog. Basisvektoren.

Wie verhalten sich dann Vektoren und ihre Komponenten bei einem Wechsel der Basisvektoren?

Im Gegensatz zum invarianten Vektor selbst, verändern sich seine Komponenten bei Änderung der Vektorbasis.

Wir sahen, dass wenn sich die Längen der Basisvektoren verlängern, sich die Komponenten von Vektoren verkleinern. Deshalb hatten wir diese Vektoren “kontravariant” genannt.

So ein kontravarianter Vektor ist ein erstes Beispiel für einen Tensor. Ein zweites Beispiel für einen Tensor sind die sog. Co-Vektoren…

Allgemein gesagt bedeutet Kontravarianz, dass wenn ein Ding größer wird, ein anderes Ding kleiner wird. Kovarianz dagegen bedeutet, dass die Veränderungen in die gleiche Richtung gehen.

Co-Vektoren

Im Gegensatz zu den “herkömmlichen” kontravarianten Vektoren, die wir als Spalte schreiben, schreiben wir Co-Vektoren als Zeilen.

Dazu hat “eigenchris” ein schönes Youtube-Video gemacht: https://youtu.be/LNoQ_Q5JQMY

In der Sichtweise von Koordinaten macht ein Co-Vektor also folgendes:

\( \Large  \left[  \begin{matrix} a & b & c  \end{matrix} \right] \cdot \left[ \begin{array}{r} x \\\ y \\\ z  \end{array} \right] = ax+by+cz \)

Abstrakt formuliert bildet ein Co-Vektor also Vektoren auf Skalare ab.

Rank 2 Tensoren

Generell soll ein Tensor ja invariant bei einer Koordinatentransformation sein.

Lediglich die “Darstellung” eines Tensors erfolgt mit Komponenten (Koordinaten).

Uns interessieren hier in erster Linie sog. Rank 2 Tensoren. Solche Rank 2 Tensoren können immer als “normale” Matrix mit Zeilen und Spalten dargestellt werden  (Zeilen und Spalten -> Rank 2). So ein Rank 2 Tensor kann aber auch ganz einfach in sog. Index-Schreibweise dargestellt werden z.B. Tij oder g μν (Anzahl Indices = Rank).

Transformationsverhalten

xyz

 

 

Computer: Mathematik – Vektorräume – Lineare Algebra

dkracht

Gehört zu: Mathematik
Siehe auch: Grundlagen,  Algebren, Matrizenrechnung, Tensor-Algebra, Relativitätstheorie, Metrik-Tensor,  Elektrisches Feld, Magnetisches Feld
Benutzt: WordPress-Plugin Latex

Stand: 27.11.2022  (Drehmoment, Archimedes, Skalarprodukt, Vektorbasis)

Youtube-Videos zur Vektor- und Tensorrechnung (für Physiker)

Youtube Videos von Prof. Wagner zur Vektor- und Tensorrechnung

  • VT I – 01 Affine und Euklidische Vektorräume:https://www.youtube.com/watch?v=NxQTRW-5vpk
  • VT I – 02 Inhalt und Winkel:https://www.youtube.com/watch?v=1cyrZZnhjjs
  • VT I – 03 Vektorbasen und Vektorkomponenten:https://www.youtube.com/watch?v=BD-Xb9Wj0I8
  • VT I – 04 Ko- und Kontravariante Vektorbasen:https://www.youtube.com/watch?v=XBMRx4rXPPg
  • VT I – 05 Anwendungen des Metriktensors:https://www.youtube.com/watch?v=okkfJEeEqk4
  • VT I – 06 Transformation zwischen Basen – Beispiele:https://www.youtube.com/watch?v=iieCaxYj2RQ
  • VT II – 01 Differentialoperatoren:https://www.youtube.com/watch?v=0tjWWS2DGmU&t=127s
  • VT II – 02 Anschauliche Interpretation der Differentialoperatoren:https://www.youtube.com/watch?v=Cyqahzn-cXw&t=3s
  • VT II – 03 Anwendungsbeispiele für Differtialoperatoren:https://www.youtube.com/watch?v=DfPGExmGRrs
  • VT II – 04 Kurven und Hyperflächen:https://www.youtube.com/watch?v=c07r4pARzHw
  • VT II – 05 Krummlinige Koordinaten:https://www.youtube.com/watch?v=yQlbJN8I6kk
  • VT II – 06 Krummlinige Koordinaten – Beispiele:https://www.youtube.com/watch?v=s1E_XeIgCpI&t=545s
  • VT II – 07 Transformationsverhalten, Tensoren:https://www.youtube.com/watch?v=srGlFECRijo&t=928s
  • VT II – 08 Bogenlänge von Kurven, Metrik:https://www.youtube.com/watch?v=2FCEKDMnKew&t=2075s
  • VT II – 09 Kovartiante Ableitung, Christoffel Symbole:https://www.youtube.com/watch?v=OnR5Ny47IXw
  • VT II – 10 Beispiele zur kovarianten Ableitung:https://www.youtube.com/watch?v=jQjsEK7GAVY
  • VT II – 11 Vektor-Differentaloperatoren in krummlinigen Koordinaten:https://www.youtube.com/watch?v=7PXs4_9RHWo&t=107s
  • VT II – 12 Eigenschaften der kovarianten Ableitung, Riemannscher Krümmungstensor:https://www.youtube.com/watch?v=I-OAGrUX580&t=429s
  • VT II – 13 Vom Riemannschen Krümmungstensor zu den Einsteinschen Feldgleichungen:https://www.youtube.com/watch?v=NqiV8SCtHCA&t=203s
  • VT II – 14 Geodätische Linien, Parallele Vektoren:https://www.youtube.com/watch?v=TfeTfqLa8vI

Vektorfelder und Skalarfelder

Was meint man mit dem Begriff “Feld”?

Das Wort “Feld” wird gerne gebraucht, wenn eigentlich eine ganz normale Abbildung (auch Funktion oder auch Verknüpfung genannt) gemeint ist – “just to confuse the Russians”.

Der Definitionsbereich so einer Abbildung ist ein “Raum”. Das kann ein sog. Euklidischer Raum oder auch eine Riemannsche Mannigfaltigkeit sein. Die Punkte (Orte) in so einem Raum kann man durch Koordinaten beschreiben.
Je nach dem ob der Wertebereich ein Vektorraum oder ein Körper (von Skalaren) ist, spricht man von “Vektorfeld” oder “Skalarfeld” und man schreibt gerne:

  • für ein skalares Feld: \( \Phi(r) \)
  • für ein Vektorfeld: \(  \vec{V}(r) \)

Wobei r ein Punkt aus dem Definitionsbereich ist (kein Vektor, sondern ein durch Koordinaten beschriebener Punkt)

Beispiele

  • Temperatur: Wenn wir jedem Punkt im Raume seine Temperatur zuordnen, haben wir ein Skalarfeld.
  • Höhe: Wenn wir jedem Punkt auf einer Landkarte die Höhe über dem Meeresspiegel zuordnen, haben wir ein Skalarfeld.
  • Wind: Wenn wir jedem Punkt auf einer Landkarte die Windrichtung und Windstärke zuordnen, haben wir ein Vektorfeld.
  • Gravitation: Wenn wir jedem Punkt im Raum die Richtung und Stärke der Gravitationskraft zuordnen (wäre mit einem kleinen Probekörper zu bestimmen), haben wir ein Vektorfeld, genannt Gravitationsfeld
  • Ein elektrisches Feld (ein Vektorfeld) gibt für jeden Punkt im Raum die Richtung und Stärke der elektrischen Kraft an, die auf ein kleines Probeteilchen der elektrischen Ladung +1 wirkt
  • Ein magnetisches Feld (ein Vektorfeld) gibt für jeden Punkt im Raum die Richtung und Stärke der magnetischen Kraft an, die auf ein kleines Probeteilchen wirkt

Visuelle Veranschaulichung von Feldern

Skalarfelder kann man beispielsweise durch Linien im Definitionsbereich, die alle einen gleichen Skalarwert haben, veranaschaulichen (z.B. Isotermen, Isohypsen etc.)

Vektorfelder veranschaulicht man sich gerne durch sog. “Feldlinien“; diese zeigen dann immer in die Richtung des Werte-Vektors. Beispiel: Feldlinien im Magnetfeld, die in Richtung der magnetischen Kraft zeigen…

Die Physiker sprechen gern von sog. Kraftfeldern. Der Begriff “Feld” hilft, die Vorstellung der Fernwirkung zu vermeiden (sagt Feynman). Die vier konzeptionellen Stufen der Kraftwirkung sind:

  • Die Kraft bewirkt eine Beschleunigung   (Newton)
  • Ein Feld bewirkt eine Kraft
  • Kraft durch Raumkrümmung (geometrische Vorstellung) (Einstein)
  • Kraft durch virtuelle Austauschteilchen

Eigenvektoren und Eigenwerte

Bei Linearen Abbildungen in den gleichen Vektorraum, also:

\(  f: V  \to V \\\)

sind Eigenvektoren dieser Linearen Abbildung Vektoren, die durch diese Abbildung nicht in ihrer Richtung verändert werden; d.h.:

\(  f(\vec{x}) = \lambda \vec{x} \\\)

und den Skalar λ nennt man dann den Eigenwert.

Häufig verwendet man Eigenvektoren und Eigenwerte, wenn die Lineare Abbildung durch eine Matrix beschrieben wird.

In der Quantenphysik spielt dies Konzept eine wichtige Rolle. Dort werden Eigenwerte als Messwerte bei einem Experiment interpretiert.

Das Skalarprodukt von Vektoren

Auf einem Vektorraum kann ein Skalarprodukt definiert sein (Vektor mal Vektor ergibt einen Skalar) –  Dies ist inspiriert aus der Physik durch Arbeit = Kraft mal Weg.

Vektorräume müssen aber nicht notwendig ein Skalarprodukt haben.

Wir werden sehen, dass so ein Skalarprodukt dann eine “Norm” induziert und damit eine Metrik, wodurch z.B. Grenzwertprozesse möglich werden.

Einen \(\mathbb{R}\)-Vektorraum mit Skalarprodukt nennt man auch einen Euklidischen Raum, einen \(\mathbb{C}\)-Vektorraum mit Skalarprodukt nennt man auch Hilbertraum – genauer Prähilbertraum.

Das innere Produkt zweier Vektoren v und w (auch Skalarprodukt oder Dot Product genannt) ist schreibt man:

\( \Large \vec{v} \cdot \vec{w} \) \( \Large \langle v,w \rangle \)

Definition des inneren Produkts

Man kann das innere Produkt geometrisch und anschaulich definieren oder aber auch mathematisch über Axiome.

Geometrische Definition

Unabhängig von einem Koordinatensystem – geometrisch definiert als:

\( \Large \vec{v} \cdot \vec{w} = ||  \vec{v} || \enspace || \vec{w} || \cos(\angle \left( \vec{v}, \vec{w} \right)) \)

Als Schlussfolgerung kann man die Länge eines Vektors auch per innerem Produkt darstellen als:

\( \Large || \vec{v} ||  = \sqrt{\vec{v} \cdot \vec{v}} \\\ \)

In einem chartesischen Koordinatensystem (s.u.) berechnet sich das innere Produkt (Skalarprodukt) der Vektoren

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right]  \) und   \( \Large \vec{w} = \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right]  \)

als   \( \Large \vec{v} \cdot \vec{w} = v_1 w_1 + v_2 w_2 + v_3 w_3 \)

Soweit haben wir das innere Produkt (Skalarprodukt) zweier Vektoren durch Winkel und Länge anschaulich definiert. Wir können auch umgekehrt Länge und Winkel durch das Skalarprodukt definieren:

Länge:

\( \Large || \vec{v} ||  = \sqrt{\vec{v} \cdot \vec{v}} \\\ \)

Winkel:

\( \Large \cos(\angle \left( \vec{v}, \vec{w} \right))  = \frac{ ||  \vec{v} || \enspace || \vec{w} ||}{ \vec{v} \cdot \vec{w}    }  \)

Das funktioniert aber nur, wenn wir schon ein Skalarprodukt haben.

Sprechweise: Tensoren statt Vektoren und Matrizen

Die Tensoren und die Tensorrechnung stammen eigentlich aus der Physik und sind für ganz praktische physikalische Problemlösungen “erfunden” worden. Ein Tensor in diesem Sinne ist einfach ein indiziertes Objekt. Die Indizes laufen normalerweise von 1 bis n, der Dimensionszahl des Raumes in dem wir arbeiten.

Ein Objekt mit einem Index wäre ein Tensor der Stufe 1, ein Objekt mit zwei Indizes ein Tensor 2. Stufe etc. Die “Objekte”, die man indiziert sind meist Reelle oer Komplexe Zahlen – allgemein gesagt Elemente eines Körpers – die man auch Skalare nennt.

Einen Tensor 1. Stufe schreibt man gerne \( a_i \) also mit einem Index – meist unten aber manchmal auch oben \( a^i \) .

Man kann so einem Tensor 1. Stufe auch einen Vektor zuordnen, wobei die indizierten Größen dann die Komponenten eines Vektors zu einer bestimmten Vektorbasis (s.u.) werden. Wenn man so einen Vektor meint, schreibt man das Ganze in Klammern – womit dann alle Komponenten des Tensors gemeint sind:

\( (a_i)  \)

Einen Tensor 2. Stufe schreibt man gerne \( {a_i}^j \) also mit zwei Indizes – teilweise unten und teilweise auch oben.

Man kann so einem Tensor 2. Stufe auch eine Matrix zuordnen, wobei die indizierten Größen dann als Zeilen und Spalten in der Matrix abgelegt werden. Wenn man so eine Matrix meint, schreibt man das Ganze in Klammern (da sind dann eben alle Komponenten drin):

\( ({a_i}^j) \\\ \)

Bei mehreren Indizes (also Tensoren der Stufe 2 und höher) ist es wichtig, dass die Reihenfolge der Indizes immer ersichtlich ist. Verwechselungsgefahr besteht ja speziell wenn man Indizes unten und oben hinschreibt.

Wenn ich zwei Tensoren 2. Stufe habe, kann ich die zugehörigen Matrizen ganz einfach multiplizieren indem wir mit der Einsteinschen Summenkonvention über den inneren Index (hier j) summieren:

\( ({a_i}^j)({b_j}^k) = ({a_i}^j \cdot {b_j}^k) \)

=========================================

Eigenschaften von Vektoren

Aus geometrischer und intuitiver Sicht spricht man auch von Längen und Winkeln:

  • Für die Länge eines Vektors (man sagt auch “Norm”) schreibt man:  \( \Large ||  \vec{v}  ||  \)
  • Für den Winkel zwischen zwei Vektoren schreibt man: \( \Large  \angle \left( \vec{v}, \vec{w} \right)  \)

Das äußere Produkt von Vektoren

Das äußere Produkt zweier Vektoren (auch Vektorprodukt oder Kreuzprodukt genannt) ist definiert als ein Vektor:

\( \Large \vec{v} \times \vec{w} = \vec{u} \)

Der Vektor u steht senkrecht auf beiden Vektoren v und w und hat die Länge \( \Large ||\vec{v}|| \cdot ||\vec{w}|| \cdot \sin(\angle \left( \vec{v}, \vec{w} \right)) \)

In einem chartesischen Koordinatensystem (s.u.) berechnet sich das äußere Produkt (Vektorprodukt) der Vektoren

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right]  \) und   \( \Large \vec{w} = \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right]  \)

als   \( \Large   \vec{v} \times \vec{w} =   \left[ \begin{array}{c} v_2 w_3 – v_3 w_2  \\\ v_3 w_1 – v_1 w_3  \\\ v_1 w_2 – v_2 w_1  \end{array} \right]        \)

Anwendungen

Eine Anwendung für das Kreuzprodukt ist beispielsweise die Kreisbewegung, wo sich die Bahngeschwindingkeit aus Winkelgeschwindigkeit ω und Radius r wie folgt ergibt:

\( \vec{v} = \vec{\omega} \times \vec{r} \\ \)

Bei der Rotation ergibt sich das sog. Drehmoment \(\vec{M}\)  aus dem Kraftvektor \(\vec{F}\) und dem Ortsvektor \( \vec{r} \) vom Bezugspunkt zum Angriffspunkt der Kraft:

\( \vec{M} = \vec{r} \times \vec{F} \)

Hierin steckt auch das aus der Schulzeit bekannte Hebelgesetz (Archimedes von Syrakus 287 v.Chr. – 212 v.Chr.): Kraft mal Kraftarm = Last mal Lastarm

Algebren

Ein Vektorraum V über einem Körper K zusammen mit einer bilinearen Abbildung:

\(  V \times V \to V \)

wird eine Algebra genannt.

Die bilineare Abblidung wird “Produkt” genannt und auch so wie ein Produkt hingeschrieben; also:  a · b  oder einfach ab. In dieser Schweibweise bedeutet die Bilinearität einfach folgendes:

\(   (x + y) \cdot z = x \cdot z + y \cdot z  \\\ \)

 

\(   x \cdot (y + z)  = x \cdot y + x \cdot z  \\\ \)

 

\( a (x \cdot y) = (ax) \cdot y = x \cdot (ay) \\\ \)

Das “besondere” an Algebren ist die “Multiplikation”. Deswegen unterscheidet man  Algebren auch nach den Eigenschaften dieser Multiplikation:

Kommutative – nicht-kommutative Algebren: Ist immer \( a \cdot b  =  b \cdot a \) oder nicht?

Assoziative – nicht-assoziative Algebren: Ist immer \( a \cdot (b \cdot c) = (a \cdot b) \cdot c \) oder nicht?

Beispiele:

Die n × n Matrizen über einem Körper mit der gewöhnlichen Matrizenmultiplikation als “Multiplikation” bilden eine (assoziative) Algebra.

Hilbertraum und Operatoren

Ein Vektorraum über \(\mathbb{R} \) oder \(\mathbb{C} \) mit einem Skalarprodukt heisst “Prä-Hilbertraum”. Wenn so ein “Prä-Hilberraum” auch noch “vollständig” ist; d.h. jede Cauchy-Folge konvergiert (bezüglich der Metrik), dann hat man einen echten Hilbertraum; Nach David Hilbert (1862-1943).

Abbildungen von einem Hilbertraum in sich selbst heissen auch “Operatoren“.

Beispiel: Differentialoperatoren

Koordinatensystem, Dimension

In einem Vektorraum V kann ich viele Koordinatensysteme haben. Jedes Koordinatensystem ist bestimmt durch eine Menge sog. Basis-Vektoren.

Dann kann jeder Vektor des Vektorraums als sog. Linearkombination aus den Basis-Vektoren dargestellt werden kann. Eine solche “Linearkombination” ist eine Summe von Basis-Vektoren, die mit geeigneten Skalaren multipliziert wurden.

Beispiel für eine Linearkombination:

\( \Large a  \vec{v} + b \vec{w} + c \vec{u} \)

Ganz genau genommen, spannt eine Basis nicht nur den ganzen Vektorraum auf (das wäre ein Erzeugendensystem), sondern enthält dabei eine minimale Anzahl von Vektoren (was äquivalent ist mit der eindeutigen Darstellung aller Vektoren des Vektorraums in Form von Linearkombinationen).

Beispiel für eine Basis (im Vektorraum \(\mathbb{R}^3\) ):

\( \hat{i} =\left[ \begin{array}{c} 1 \\\ 0 \\\ 0  \end{array} \right]   \hat{j} =\left[ \begin{array}{c} 0 \\\ 1 \\\ 0  \end{array} \right] \hat{k} =\left[ \begin{array}{c} 0 \\\ 0 \\\ 1  \end{array} \right] \)

Und man schreibt dann auch gerne:

\( \Large \vec{v} = \left[ \begin{array}{c} x \\\ y \\\ z  \end{array} \right] = x \hat{i} + y \hat{j} + z \hat{k}\)

Ein Vektorraum kann mehrere Basen haben, die jeweils ein Koordinatensystem definieren. Dabei werden die Koordinaten (Komponenten) ein und desselben Vektors in verschiedenen Koordinatensystem auch verschieden sein, der Vektor selbst aber ist “invariant”. Wenn man einen Vektor als Liste von Koordinaten hinschreibt, muss man immer sagen. welche Basis gemeint ist.

Ein Vektorraum kann mehrere Basen haben, aber die Anzahl der Vektoren in einer Basis ist immer die gleiche. Diese Anzahl nennt man “Dimension” des Vektorraums und schreibt:

Dimension des Vektorraums V: dim(V)

Beschreibung durch Basis-Vektoren: Lineare Transformationen

Eine Lineare Transformation kann eindeutig beschrieben werden durch die Werte auf die die Basis-Vektoren abgebildet (transformiert) werden.

Beispielsweise heisst das im Vektorraum \(\mathbb{R}^2\) mit dem kanonischen Koordinatensystem und den Basisvektoren \( \hat{i} \) und \( \hat{j}  \) folgendes:

Wenn wir einen Vektor \( \vec{v} = \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x \hat{i} + y\hat{j} \) betrachten, so wirkt eine Lineare Transformation L wie folgt:

\( L(\vec{v}) = x L(\hat{i}) + y L(\hat{j} )  \)

Wenn wir also die transformierten Basisvektoren \( L(\hat{i}) \) und \( L(\hat{j}) \)  kennen, ist damit die Lineare Transformation L vollständig festgelegt.

Diese transformierten Basis-Vektoren können im verwendeten Koordinatensystem als Matrix schreiben.

Wenn bei unserer Linearen Transformation beispielsweise \( L(\hat{i}) = \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] \)   und \( L(\hat{j}) = \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] \)  wäre, bekämen wir eine Matrix:

\(\left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right] \)

Wir schreiben also in den Spalten der Matrix die transformierten Basisvektoren.
Die Lineare Transformation könnte im benutzten Koordinatensystem als Matrixmultiplikation aufgefasst werden:

\(\left[ \begin{array}{rr} 3 & 2 \\  -2 & 1 \\  \end{array} \right]  \left[ \begin{array}{c} x \\\ y  \end{array} \right] = x  \left[ \begin{array}{c} 3 \\\ -2  \end{array} \right] + y  \left[ \begin{array}{c} 2 \\\ 1  \end{array} \right] = \left[ \begin{array}{c} 3x+2y \\\ -2x+1y  \end{array} \right]\)

Völlig analog werden auch Lineare Transformationen in drei oder mehr Dimensionen behandelt.

Beschreibung durch Basis-Vektoren: Wechsel von Koordinatensystemen

Wenn wir zwei Koordinatensysteme betrachten, dann haben die also zwei Basen (wir nennen sie “alte Basis” und “neue Basis”). Intuitiv ist klar, dass wenn die neue Basis z.B. längere Basisvektoren hat, dann sind die Vektorkomponenten kürzer (weil ja der gleiche Vektor wieder herauskommen soll). Die Vektorkomponenten verhalten sich also “umgekehrt” wie die Längen der Basisvektoren. Deshalb nennt man diese Vektoren “kontravariant“.

Wir können das auch haarklein ausrechnen:

  • Die “alte Basis” sei: \( \vec{e}_i  \)
  • Die “neue Basis” sei: \( \tilde{\vec{e}}_i  \)

Dann transformieren sich die Basisvektoren wie folgt:

Alt -> Neu (“Foreward”):

\(  \tilde{\vec{e}}_i =  \sum\limits_{k=1}^{n} F_{ki} \vec{e_k}\)

Neu -> Alt (“Backward”):

\(  \vec{e}_i =  \sum\limits_{j=1}^{n} B_{j i} \widetilde{\vec{e_j}}\)

Für die Komponenten eines Vektors \( \vec{v} \) gilt dann die umgekehrte Richtung (deshalb nennt man sie “kontravariant“)

Alt -> Neu:

\( \tilde{v_i} = \sum\limits_{j=1}^{n} B_{ij} v_j  \)

Neu -> Alt

\( v_i = \sum\limits_{j=1}^{n} F_{ij}\tilde{v_j}   \)

Berechnung der Länge eines Vektors aus seinen Komponenten

Länge eines Vektors im Chartesischen Koordinatensystem

Wir sind ja gewöhnt, die Länge eines z.B. dreidimensionalen Vektors über seine Koordinaten und den Lehrsatz des Pythagoras zu berechnen:

Im Beispiel sei der Vektor \( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] \)

Dann wäre die Länge dieses Vektors gegeben durch: \( || \vec{v} ||= \sqrt{v_1^2 + v_2^2 + v_3^2} \)  (der gute alte Pythagoras)

In verschiedenen Koordinatensystemen würde dieser Vektor aber mit verschiedenen Koordinaten (Komponenten) beschrieben und es würden mit obiger Formel dann unterschiedliche Längen heraus kommen.

Uns ist ja klar, dass wir zu den Koordinaten (Komponenten) eines Vektors auch immer angeben müssen, in welchem Koordinatensystem diese gemessen werden; d.h. wir müssen zu den Koordinaten die dazugehörige Basis angeben – und berücksichtigen.

Wenn wir als Basis allgemein schreiben: \( \vec{e}_i  \)

dann können wir mit den Komponenten unseres Vektors zu dieser Basis schreiben:

\( \Large \vec{v} = \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] = v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3\)

Im Spezialfall der orthonormalen Basis:

\( \vec{e}_1 = \hat{i}, \vec{e}_2 = \hat{j}, \vec{e}_3 = \hat{k}   \)

hätten wir die Länge unseres Vektors nach Pythagoras (s.o.); mit den Koordinaten zu einer anderen Basis müssten wir umrechnen…

Länge eines Vektors in einem beliebigen Koordinatensystem

Wir hatten die Länge eines Vektors unabhängig von einem Koordinatensystem (also invariant) definiert über:

\( \Large {||  \vec{v}  ||}^2 = \vec{v} \cdot \vec{v} \\\)

Wir nehmen jetzt ein beliebiges Koordinatensystem definiert durch seine Basisvektoren \( \vec{e}_i\).
Dann können wir die Länge des Vektors wie folgt aus seinen Komponenten (Koordinaten) berechnen:

\( \Large  ||  \vec{v} ||^2 = (v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3) \cdot(v_1 \vec{e}_1 + v_2 \vec{e}_2 + v_3 \vec{e}_3) \\ \)

Wenn wir das ausmultiplizieren bekommen wir:

\( \Large ||  \vec{v} ||^2 =  \sum\limits_{ij} v_i v_j  \enspace \vec{e}_i \cdot \vec{e}_j \\ \)

Um die Länge eines Vektors in einem beliebigen Koordinatensystem zu ermitteln, benötigen wir also “lediglich” alle Kombinationen der inneren Produkte der Basisvektoren dieses Koordinatensystems; d.h. alle \( \vec{e}_i \cdot \vec{e}_j \)

Als Matrix können wir diese Produkte so hinschreiben:

\(\Large g =  \left[ \begin{array}{rrr} \vec{e}_1 \cdot \vec{e}_1 & \vec{e}_1 \cdot \vec{e}_2 & \vec{e}_1 \cdot \vec{e}_3\\  \vec{e}_2 \cdot \vec{e}_1 & \vec{e}_2 \cdot \vec{e}_2 & \vec{e}_2 \cdot \vec{e}_3 \\  \vec{e}_3 \cdot \vec{e}_1 & \vec{e}_3 \cdot \vec{e}_2 & \vec{e}_3 \cdot \vec{e}_3 \end{array} \right]  \\\)

Diese Matrix g nennt man auch den Metrik-Tensor des Koordinatensystems.

Mit Hilfe dieses Metrik-Tensors ergibt sich dann die Länge des Vektors \(\vec{v}\) ganz einfach als Matrixprodukt:

\(\Large || \vec{v} ||^2  =  \left[ \begin{array}{c} v_1 & v_2 & v_3  \end{array} \right]  g  \left[ \begin{array}{c} v_1 \\\ v_2 \\\ v_3  \end{array} \right] \\\)

Ganz allgemein kann man mit diesem Metrik-Tensor das innere Produkt zweier Vektoren aus den Komponenten berechnen:

\( \Large \vec{v} \cdot \vec{w} =  \left[ \begin{array}{c} v_1 & v_2 & v_3  \end{array} \right]  g  \left[ \begin{array}{c} w_1 \\\ w_2 \\\ w_3  \end{array} \right] \)

Das funktioniert, weil der Metrik-Tensor nicht “irgendeine” Matrix ist, sondern “invariant” ist; d.h. unabhängig vom gewählten Koordinatensystem kommt immer das gleiche Ergebnis heraus.

Der Metrik-Tensor

Der Metrik-Tensor definiert also eine (bilineare) Abbildung:

\(  g: V \times V \to \mathbb{R} \\\)

Ein Metrik-Tensor ist eine spezielle Bilineare Abbildung, die erstens symmetrisch ist und zweitens immer positive Werte liefert.

Dies ist auch im Prinzip der Metrik-Tensor, der in den Einsteinschen Feldgleichungen als \( g_{\mu \nu} \) vorkommt.

Oben hatten wir das innere Produkt zweier Vetoren ja versucht unabhängig von einem Koordinatensystem zu definieren.
Man kann das Ganze nun aber auch umgekehrt “aufzäumen”.  Wenn wir einen Vektorraum und eine Basis haben (damit also ein Koordinatensystem), brauchen wir nur noch einen Metrik-Tensor “g” und können damit ein inneres Produkt zwischen zwei Vektoren v und w als schlichte Matrix-Multiplikation definieren:

\( \Large \vec{v} \cdot \vec{w} =  \vec{v}^T   \enspace g  \enspace \vec{w} \\ \)

Wobei das hochgestellte T “transponiert” meint. So wird aus einem Spaltenvektor ein Zeilenvektor.

Beispielsweise definiert der folgende Metrik-Tensor die übliche Metrik für alle Koordinatensysteme mit einer orthonormaler Basis – denn das innere Produkt verschiedener Basisvektoren ist Null (weil orthogonal) und das innere Produkt eines Basisvektors mit sich selbst ist 1 (weil Länge 1):

\(\Large g =  \left[ \begin{array}{rrr} 1 & 0 & 0\\  0 & 1 & 0 \\  0 & 0 & 1 \end{array} \right]  \\\)

Das gilt z.B. für ein “normales” Koordinatensystem im Euklidischen Raum.
Mit dieser Metrik ist die Länge eines Vektors also:
\( || \vec{v} ||^2 = v_1^2 + v_2^2 + v_3^2 \)
und diese Länge ist invariant gegenüber Koordinatentransformationen.

Und eine Minkowski-Metrik wird definiert durch den Metrik-Tensor:

\(\Large \eta =  \left[ \begin{array}{rrrr} 1 & 0 & 0 & 0\\  0 & -1 & 0  & 0\\  0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array} \right]  \\\)

Mit dieser Metrik wäre die Länge eines Vektors also gegeben durch:

\( || \vec{v} ||^2  =  v_1^2 – v_2^2 – v_3^2 – v_4^2\)

Diese so definierte Länge wäre invariant gegenüber Lorentz-Transformationen, die wir später in der Speziellen Relativitätstheorie kennenlernen werden.

Was ist ein Tensor?

Der oben beschriebene Metrik-Tensor ist ein Tensor vom Rank 2. D.h. eine zweidimensionale (also “normale”) Matix, die sich bei Transformation der Koordinatensysteme “freundlich” verhält, sodass wir von “Invarianz” sprechen können.

Allgemein und formal ist ein Tensor T eine multilineare Abbildung von einem cartesischen Produkt von Vektorräumen über einem gemeinsamen Körper von Skalaren in diesen Skalaren-Körper:

\( T: V_1 \times V_2 \times … \times V_n \to K \)

Wobei die \(V_i\) Vektorräume über K sind.

Das allgemeine Thema “Tensor” ist mathematisch vielschichtig, deshalb habe ich begonnen, einen separaten Artikel darüber zu geschrieben.

Link: https://youtu.be/8ptMTLzV4-I

Determinante und Rank

Diese Konzepte werden in Video 6 und Video 7 behandelt.

Bei einer Linearen Transformation wird die Fläche des Quadrats aus den Basisvektoren  um einen Faktor “transformiert”. Damit wird auch jede beliebige Fläche um diesen Faktor “transformiert”. Diesen “Faktor” nennen wir die Determinante der Linearen Transformation.

Entsprechend ist das auch in höheren Dimensionen z.B. mit drei Dimensionen, wo die Größe des Volumens transformiert wird.

Eine negative Determinante bedeutet, dass sich bei der linearen Transformation die “Orientierung” des Vektorraums umkehrt.

Der Rank meint die Dimension des Ausgaberaums einer Linearen Transformation. Wenn der Rank einer Transformation nicht die volle Dimension (“full rank”) unseres Vektorraums ist, ist die Determinante dieser Transformation natürlich Null, aber der Rank kann etwas differenzierter aussagen was da los ist z.B. der Rank einer 3-dimensionalen Matrix (Transformation) könnte 2 sein, dann ist der Ausgaberaum eine Ebene (2 Dimensionen), wenn der Rank 1 wäre, hätten wir als Ausgaberaum eine Linie (eine Dimension) etc. Dieser “Ausgaberaum” wird auch “Column Space” genannt, weil die Spaltenvektoren diesen aufspannen…

 

Computer: Mathematik – Statistik

dkracht

Mathematik: Statistik (aus Wiki)

Immer wieder werde ich als gelernter Mathematiker nach elementaren Themen der Statistik gefragt.

Ich habe einen schönen Einführungskurs in die Statistik bei der Universität Newcastle, Australien, gefunden:

http://www.anu.edu.au/nceph/surfstat/surfstat-home/t-table.html

http://www.anu.edu.au/nceph/surfstat/surfstat-home/

Statistik

Typen von Variablen (“Metriken”)

Qualitativ / Quantitativ

Man spricht von “qualitativen” Variablen, wenn die Beobachtungen durch Kategorien beschrieben werden.
Beispiele:

  • Augenfarbe: braun, grau, blau,…
  • Delivery Model: insourced, outsourced
  • Performance Rating: Less than Acceptable, Inconsistent, Fully Successful, Exceeds, Exceptional

Eine qualitative Variable heist “ordinal”, wenn es eine natürliche Reihenfolgebeziehung zwischen den Kategorien gibt, (Beispiel: Performance Rating).

Eine qualitative Variable heisst “nominal”, wenn es keine natürliche Reihenfolgebeziehung gibt, (Beispiel: Augenfarbe).

Man spricht von “quantitativen” Variablen, wenn die Beobachtungen durch numerische Werte beschrieben werden, d.h. durch Zählen oder Messen zustande kommen.
Beispiele:

  • Alter
  • Körpergröße
  • Anzahl Personen im Haushalt
  • Anzahl gerauchter Zigaretten am Tag
  • Einkommen im Jahr

Eine quantitative Variable heisst “diskret”, wenn die Beobachtungen ganzzahlige Werte sind (Beispiel: Anzahl Personen im Haushalt).

Eine quantitative Variable heisst “stetig” (continous), wenn sie durch (im Prinzip) beliebige Zahlen dargestellt wird (Beispiel: Körpergröße).

Normalverteilung mit Perzentil

Fragestellung zu einer Normalverteilung N(My,Sigma):

  • Gegeben sei My und P25
  • Gesucht ist Sigma
  • Lösung: sigma = (P25 – My) / NormInv(0,25; 0; 1)

Im übrigen gilt sowieso: P25 = NormInv(0,25; My; Sigma)

Logarithmische Normalverteilung

Zur Logarithmischen Normalverteilung habe ich einen gesonderten Artikel geschrieben.

Beta-Verteilung

Zur Beta-Verteilung habe ich einen gesonderten Artikel geschrieben.

— Dkracht 12:29, 24 March 2008 (CET)