Astrofotografie: Belichtungszeit, Lichtverschmutzung und Rauschen

Gehört zu: Astr ofotografie
Siehe auch: Stacking, Nachführung Autoguiding, PHD2 Guiding, Lichtverschmutzung, SQM Sky Quality Meter, Hintergrundlimitiert, Fitswork, GeoGebra
Benötigt: WordPress Latex-Plugin , Fotos von Google Drive, Grafiken von Github

Stand: 12.10.2022 (GeoGebra)

Wie erziele ich gute Astro-Fotos?

Das hier betrachtete Qualitätskriterium ist das “Signal-Rausch-Verhältnis” (Signal to Noise Ratio = SNR). Die Qualität von Astro-Fotos wird generell von vielen Faktoren beeinflusst. Darunter sind beispielsweise:

CCD- oder CMOS-Kamera
Farb-Sensor oder Mono-Sensor
Geregelte Kühlung des Sensors (DSLR oder Dedizierte Astro-Kamera oder WebCam oder ?)
Belichtungszeit
Lichtverschmutzung am Beobachtungsort
Fokussierung
Nachführung (z.B. keine, nur Tracking, Autoguiding,…)
Filter
…

Dieser Artikel beschäftigt sich schwerpunktmäßig mit den Belichtungszeiten bei DSO-Aufnahmen und der Frage, wie dafür das Signal-Rausch-Verhältnis verbessert werden kann.

Wie lange sollten die einzelnen Sub-Exposures belichtet werden?

Wir haben ja gelernt, dass wir sehr lange Belichtungszeiten für die so lichtschwachen Objekte (DSOs) der Astrofotografie brauchen.

Lange Belichtungszeit heisst hier aber nicht notwendig, dass ein einzelnes Foto lange belichtet werden muss, sondern wir können auch viele Einzelaufnahmen (Sub Exposures) machen und die dann aufaddieren (Stacken). Es kommt auf die Summe der Einzelbelichtungen an. Man sagt, die gesammte “Integrationszeit” ist das Wesentliche.

Diese Integrationszeit sollte in der Tat lang sein; d.h. mindestens 1 Stunde, besser 2 Stunden, besser 4 Stunden… Die Gesamtzeit (Integrationszeit) kann man ja Planen für die Bobachtungsnacht. Nehmen wir mal an, wir hätten 2 Stunden (also 120 Minuten) angesetzt. Die Frage wäre dann ja, wie lang man jedes Einzelfoto (Sub Exposure) belichten soll. Also ist 120 x 60 sec gut oder 720 x 10 sec oder 24 x 5 min oder… besser?

Quellen

Auf der “Practical Astronomy Show” am 9. März 2019 hat Dr. Robin Glover (SharpCap) dazu einen interessanten Vortrag gehalten. Der Titel des Vortrags war “Deep Sky CMOS Imaging” und er ist als Youtube-Video verfügbar. Youtube:

Chris van den Berge hat auf DSLR Astrophotography gepostet: http://dslr-astrophotography.com/long-exposures-multiple-shorter-exposures/

Ich versuche in diesem Artikel, den Vortrag von Robin Glover nachzuvollziehen und dann zu sehen, wie ich die Schlussfolgerungen auf meine persönliche Situation anpassen kann/muss. Aus diesem Grund bin ich etwas formaler und detaillierter in den Formeln…

Was ist beeinflussbar?

Wenn vieles als gegeben hingenommen werden muss, wie z.B. der Standort (und damit die Lichtverschmutzung), die Kamera (und damit das Kamera-Rauschen, die Kühlungsmöglichkeiten, die Pixelgröße etc.), die nutzbare Zeit am Abend (und damit die Gesamtbelichtungszeit), die Nachführung (keine, Tracking, Guiding,…), dann bleibt als Einflussmöglichkeit im wesentlichen die Entscheidung für die Belichtungszeit der Einzelfotos (Sub Exposures), die zum Gesamtbild zusammengeführt werden sollen (“Stacking”).

Wir gehen die Thematik in folgenden Schritten an

Grundlagen der digitalen Astrofotografie
Was beeinflusst die Qualität von Einzelfotos (Sub Exposures) ?
Wie ergibt sich die Qualität des Summenfotos (gestacktes Bild) ?
Welche Schlussfolgerungen/Empfehlungen ergeben sich daraus für den “Standard Observer”?
Welche Schlussfolgerungen/Empfehlungen ergeben sich daraus für meine persönlich präferierten Beobachtungsorte?

Grundlagen: Signal und Rauschen

Der digitale Sensor – schematisch

Abbildung 1: Elektronische Bauelemente für digitales Fotografieren (Github: dslr.svg)

Signalstärke

Auf einem Astrofoto kommen verschiedene Signale zusammen:

Ein Signal vom eigentlichen Beobachtungsobjekt (Nutz-Signal)
Ein zusätzliches Signal vom Himmelshintergrund (Light Pollution)
Ein zusätzliches Signal durch den Dunkelstrom (abhängig von der Sensor-Temperatur)

Die Signalstärke ist eigentlich: Anzahl Photonen pro Pixel pro Sekunde. Das menschliche Auge speichert die Lichtteilchen nicht, der Helligkeitseindruck (die physiologische Signalstärke) wird durch die Anzahl Lichtteilchen pro Zeiteinheit bestimmt. Das Auge hat dabei eine quasi konstante “Belichtungszeit” von so etwa 1/18 Sekunde.

Der Sensor in unserer Kamera hat im Gegensatz zum menschlichen Auge ein beträchtliches Speichervermögen. Daher ist die Belichtungszeit relevant. Die Photonen schlagen Elektronen aus dem Sensormaterial heraus und diese werden über die Belichtungszeit gesammelt. Die gesammelten Elektronen werden dann gemessen und von einem Analog to Digital Converter (ADC) in eine Zahl umgewandelt (ADU). Die Quantum Efficiency (QE) ist dabei der Prozentsatz von Photonen, der ein Elektron auslöst.

Die Signalstärke im Sensor ergibt sich aus der Signalrate und der Belichtungszeit. Wenn wir die Signalrate messen in Anzahl Elektronen pro Pixel pro Sekunde (e-/Pixel/s), ergibt sich die Signalstärke als:

Signalstärke = Signalrate * Belichtungszeit

Jedes Signal ist mit einem Rauschen behaftet. Die Signale vom Himmelshintergrund und vom Dunkelstrom können wir abziehen; es bleibt das Rauschen von Himmelshintergrund und Dunkelstrom; diese können wir durch Stacking der Light-Frames und Dark-Frames (s.u.) bekämpfen.

Messen von Signal und Rauschen

Ein mit einem digitalen Sensor gemachtes Bild besteht aus vielen Pixeln und jeder Pixel hat einen Helligkeitswert (ADU), den der ADC für das jeweilige Pixel ausgegeben hat.

Als Signal kann man nun den Mittelwert und als Rauschen die Standardabweichung dieser ADU-Werte nehmen. Dies können wir z.B. mit der Software Fitswork folgendermassen messen:

Wir öffnen das betreffende Foto in Fitswork
Wir markieren den zu messenden Bereich durch ziehen mit der rechten Maustaste (bzw. wir messen das ganze Bild)
Rechtsklick öffnet ein Kontextmenü, wo wir “Statistik für den Bereich” auswählen…

In der Astrofotografie definiert man nun das Signal to Noise Ratio (SNR) einfach als:

\(SNR = \Large \frac{Average(ADUs)}{Standard Deviation(ADUs)}\)

Rauschen

Es gibt mehrere Beiträge für Rauschen in den Light-Frames (Einzelfotos, Sub Exposures), die sich pro Einzelfoto in bestimmter Art addieren (s. unten):

Kamera-extern hat man
- Rauschen im eigentlichen, externen Signal vom Beobachtungsobjekt das sog. Shot Noise (auch Photonenrauschen oder Schrotrauschen genannt)
- Rauschen im Signal des Himmelshintergrunds (Lichtverschmutzung etc.)
Kamera-intern hat man (sog. Kamera-Rauschen):
- Rauschen durch den Auslese-Vorgang (sog. Read Noise – nur Rauschen, kein Signal)
- Rauschen durch Wärme im Sensor (sog. Thermisches Rauschen, also Rauschen im Dunkelstrom-Signal, deshalb auch Dunkelstrom-Rauschen genannt)
- Quantisierungsrauschen durch den ADC (dieses ist so gering. dass wir es in dieser Betrachtung komplett ignorieren)

Rauschen bringt feine Details im Bild zum Verschwinden. Deshalb wollen wir das Rauschen insgesamt reduzieren.

Das Rauschen ist meistens zufällig (stochastisch) und kann also dadurch bekämpft werden, dass man viele Aufnahmen macht und die dann mittelt (siehe: Stacken).

Ausser in den Einzelfotos (Light Frames) hat man auch noch Rauschen:

Rauschen in den Dark-Frames
Rauschen in den Flat-Frames

Dieses betrachten wir zunächst ebenfalls nicht.

Zusammenfassung (Executive Summary)

Da die technischen Zusammenhänge doch sehr komplex und vielschichtig sind, hier die “wichtigsten” Erkenntnisse vorweg (für einen gegebenen Standort mit gegebener Lichtverschmutzung):

Die Gesamtbelichtungszeit (Integrationszeit) muss lang sein (z.B. 2 Stunden oder mehr)
Die Belichtungszeit eines Einzelfotos muss immer so gewählt werden, dass im Histogramm weder links noch rechts etwas abgeschnitten (“geclippt”) wird
Die Einzelbelichtungszeit muss nur so groß sein, dass das Einzelbild “hintergrundlimitiert” ist; d.h.
- Unter lichtverschmutztem Himmel die Einzelfotos (Subs) kurz belichten (z.B. 30 sec), dann aber ganz viele machen (und man braucht vielleicht garkein Autoguiding)
- Unter dunklerem Himmel können die Einzelfotos schon länger belichtet werden (z.B. 5 min), wenn das Guiding (oder: Autoguiding) das hergibt
Ruhig ISO bzw. Gain hochdrehen, dann wird das Ausleserauschen geringer (bei CMOS Sensoren) – aber der Dynamik-Umfang wird etwas sinken
Das thermische Rauschen ist häufig viel kleiner als Stör-Signale aus anderen Quellen. Deshalb ist extreme Kühlung manchmal garnicht so wichtig.

Folgende Rausch-Anteile werden wir im Folgenden ignorieren:

Das thermische Rauschen im Light-Frame: Durch ausreichende Kühlung des Sensors werden wir es auf 10% der Lichtverschmutzung begrenzen
Das Dunkelstrom-Rauschen im Dark-Frame: Wird reduziert durch das Stacken vieler Dark-Frames zu einem Masterdark

Die verbleibenden Rauschanteile wollen wir durch geeignete Wahl der Belichtungszeiten soweit reduzieren, dass sie unterhalb einer persönlichen Qualitätsgrenze liegen. Dabei werden wir die Größe der Lichtverschmutzung als Massstab nehmen.

Das Ausleserauschen (Read Noise) wird irrelevant, wenn wir die Subs so lange belichten, das sie quasi “hintergrundlimitiert” werden; soll heissen dass im gestackten Bild das Ausleserauschen maximal 5% der Lichtverschmutzung ausmacht.
Das “Shot Noise” (Photonen-Rauschen) wird reduziert durch das Stacken vieler Light-Frames

Was bedeutet “hintergrundlimitiert” ?

Mit “Hintergrund” meint man die Himmelshelligkeit (Lichtverschmutzung, Airglow etc.). Unter “limitiert” durch den Hintergrund meint man, dass man nicht länger belichten sollte da bei längerer Belichtung die Lichtverschmutzung dominieren würde. Bleibt man knapp unter dieser Grenze so sind die anderen Rausch-Signale (Auslese-Rauschen und thermisches Rauschen) deutlich kleiner sind als das Signal vom Himmelshintergrund und sie können damit vernachlässigt werden. Effektiv ergibt also der Himmelshintergrund das Limit für die Belichtungszeit.

Wenn man sich nach der “optimalen” Belichtungszeit für die Subs fragt, reicht es, wenn man gerade so lange belichtet, dass die Subs hintergrundlimitiert sind. Dann wird durch noch längere Belichtungszeiten das Signal-Rausch-Verhhältnis im Stack (Summenbild) nicht mehr verbessert.

Signalkomponenten im Einzelfoto

Wir haben folgende Signalkomponeten in jedem Einzelfoto (Sub Exposure):

Signal vom eigentlichen Himmelsobjekt (ObjektSignal)
Signal vom Himmelshintergrund (LightPollutionSignal)
Signal vom Dunkelstrom

Wie addieren sich die Signalkomponenten im Einzelfoto?

Unahhängige Signale, die über die Zeit prinzipiell gleich bleiben, addieren sich “normal”.

\((1) \hspace{1 em} S_{1+2} = S_1 + S_2 \)

Addieren wir alle Signale, die wir in unserem Einzelfotohaben kommen wir zu einem Gesamtsignal (ImageSignal) von:

\((2) \hspace{1 em} ImageSignal = ObjektSignal + LightPollutionSignal + DunkelstromSignal \)

Signal vom Himmelsobjekt

Das Himmelsobjekt, welches wir fotografieren, sendet einen Strom von Photonen, die über unsere Optik auf den Pixeln des Kamera-Sensors landen und dort als Elektronen über die Dauer unserer Belichtungszeit gesammelt werden. Durch die Ausleseelektronik der Kamera erhalten wir dann pro Pixel einen Zahlenwert für die Helligkeit.

\((3) \hspace{1 em} ObjektSignal = ObjektSignalRate * Belichtungszeit \)

Je nach anvisiertem Objekt kann die “ObjektSignalRate” ganz unterschiedlich sein. Beispiel: Wieviel Photonen fallen vom Andromedanebel pro Sekunde auf ein Pixel meiner Kamera? Vermutlich könnte man aus der Flächenhelligkeit eines Objekts diese “ObjektSignalRate” ermitteln – ähnlich wie im nächsten Abschnitt mit der Lichtverschmutzung…

Signal vom Himmelshintergrund

Die Helligkeit des Himmelshintergrunds hängt von der Lichtverschmutzung am Beobachtungsort ab. Hinzu kämen der Mond, möglicherweise Airglow u.a.
Die Signalrate, gemessen in Anzahl Elektronen per Pixel per Sekunde, hängt zusätzlich von der Optik (Öffnungsverhältnis) und dem Sensor (Mono/Colour, Pixelgröße, Quanteneffizienz) ab.

Wir definieren deshalb einen “Standard-Beobachter” (mit Standard Equipment), um zu vergleichbaren Zahlen zu kommen.

Der Standard-Beobacher sei definiert durch:

Sensor: CMOS, monochrom, 50% QE, Pixelgröße 3,75µ, Temperatur 25 Grad Celsius
Öffnungsverhältnis: f/6
Lichtverschmutzung: Bortle 5
Gesamtbelichtungszeit: 60 Minuten

Die “LightPollutionRate” können wir mit dem “Sky Background Calculator” ermitteln. Link: https://tools.sharpcap.co.uk

Der Kniff dabei ist, die Himmelshelligkeit von Magnituden pro Quadratbogensekunde umzurechnen in Candela pro Quadratmeter (cd/m²). Dann haben wir einfache lineare Zusammenhänge. Die Umrechnung in cd/m² habe ich in meinem Blog-Artikel über SI-Einheiten beschrieben.

Tabelle 1: Signalrate aus Lichtverschmutzung in e- / Pixel /Sekunde (am 24.5.2021 der o.g. Website entnommen)

	Bortle 9 16.0 mag Inner City	Bortle 8 18.0 mag City Sky	Bortle 7 18.3 mag Urban	Bortle 6 18.8 mag Bright Suburban	Bortle 5 19.8 mag Suburban	Bortle 4 20.9 mag Rural/Suburban	Bortle 3 21.4 mag Rural	Bortle 2 21.6 mag typical dark	Bortle 1 21.85 mag Excellent Dark
f/4	175,25	27,78	21,07	13,29	5,29	1,92	1,21	1,01	0,80
f/5	112,16	17,78	13,48	8,51	3,39	1,23	0,78	0,65	0,51
f/6	77,89	12,34	9,36	5,91	2,35	0,85	0,54	0,45	0,36
f/7	57,23	9,07	6,88	4,34	1,73	0,63	0,41	0,33	0,26
f/10	28,04	4,44	3,37	2,13	0,85	0,31	0,19	0,16	0,13

Dies sind Daten für einen Mono-Sensor mit 50% Quantum Efficiency und 3,75μ Pixelgröße (für den sog. Standard-Observer).
Für einen Colour-Sensor sind diese Zahlen durch 3 zu dividieren.

Unser Standard-Observer hat nach Tabelle 1 also eine Lichtverschmutzung von:

\((4) \hspace{1 em} LightPollutionRate = 2.35 \space Elektronen \space pro \space Pixel \space pro \space Sekunde \)

Das am Sensor gemessene Signal steigt mit der Belichtungszeit:

\((5) \hspace{1 em} LightPollutionSignal = 2.35 \cdot Belichtungszeit \)

Signal vom Dunkelstrom

Das Signal, was der Sensor ohne einkommende Photonen macht, – also “im Dunklen” – kann man sich in einem Dark-Frame betrachten. Darauf werden Hot Pixel und evtl. ein Amp Glow zu sehen sein…

Rauschkomponenten im Einzelfoto

Wir haben folgende Rauschkomponeten in jedem Einzelfoto (Sub Exposure):

Rauschen im Dunkelstrom (ThermalNoise)
Ausleserauschen (ReadNoise)
Schrot-Rauschen (ShotNoise)
Rauschen in der Lichtverschmutzung (SkyNoise)

Wie addieren sich Rauschkomponenten im Einzelfoto?

Unahhängige Rausch-Signale, die sich über die Zeit zufällig (stochastisch) verhalten, addieren sich mit einer “Quadratwurzel” …. R₁ + R₂ = Wurzel aus (R₁ Quadrat + R₂ Quadrat)

\((6) \hspace{1 em} R_{1+2} = \sqrt{ R_1^2 + R_2^2} \)

Wenn wir zwei zufällige und unabhängige Rauschsignale R₁=4 und R₂=3 addieren, so erhalten wir R₁ + R₂ = 5
Das bedeutet, dass bei der Addition stark unterschiedlicher Rauschsignale man das schwächere “praktisch” vernachlässigen kann. Z.B. mit R₁ = 10 und R₂ =1 ergibt sich:

\((7) \hspace{1 em} R_{1+2} = \sqrt{ 10^2 + 1^2} = \sqrt{101} = 10,05 \\\ \)

Das Gesamtrauschen in einem Einzelfoto wäre also:

\((8) \hspace{1 em} ImageNoise = \sqrt{ThermalNoise^2 + ReadNoise^2 + ShotNoise^2 + SkyNoise^2} \)

Wir werden sehen, dass wir (unter bestimmten Bedingungen) das Thermische rauschen und das SkyNoise vernachlässigen können.

Thermal Noise (Dunkelstrom-Rauschen)

Im Sensor entstehen Elektronen nicht nur durch die ankommenden Photonen, sondern auch durch Wärme in der Kamera. Das nennt man “Dunkelstrom”. Dieser Dunkelstrom macht ein Dunkelstrom-Signal und ein Dunkelstrom-Rauschen (Thermal Noise). Das Dunkelstrom-Signal kann man durch Dark-Frames vom vom Nutzsignal (Light Frame) abziehen; das Dunkelstrom-Rauschen bleibt aber erhalten. Es ist von der Temperatur und der Dauer der Belichtung abhängig.

Dunkelstrom-Rauschen (Thermal Noise) verdoppelt sich ungefähr bei Temperaturerhöhung um 6,5 Grad Celsius.

Je nach Sensor ergeben sich unterschiedliche Kurven für dieses Thermal Noise (Copyright Dr. Robin Glover):

Abbildung 2: Dunkelstrom-Rauschen bei verschiedenen Temperaturen (Google Drive: RobinGlover-01.jpg)

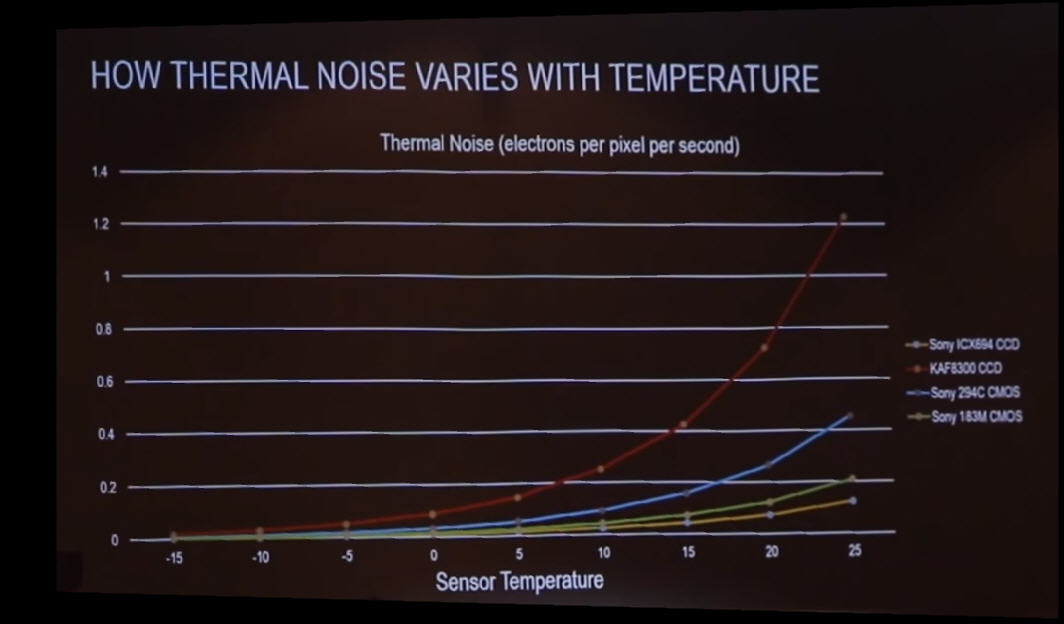
Typisch für moderne CMOS-Sensoren wie Sony 294C sind 0,2 Elektronen pro Sekunde pro Pixel bei einer Sensor-Temperatur von 25 Grad Celsius. Wenn man diese Kurven sieht, erkennt man, dass ein Herunterkühlen von 25 Grad auf 15 Grad völlig ausreicht, um das thermische Rauschen bedeutungslos (von 0,2 auf 0,1 e^–/sec) zu machen.

Bekämpfung: Das thermische Rauschen bekämpfen wir durch Kühlung des Sensors. Robin Glover empfiehlt, das thermische Rauschen auf 10% des Signals der Lichtverschmutzung zu limitieren. Bei besonders geringer Lichtverschmutzung wäre also eine entsprechende leichte Kühlung notwendig. Welche Signalstärke durch Lichtverschmutzung entsteht, ist unten beschrieben.

Erforderliche Kühlung

Um das “Thermal Noise” (das Dunkelstromrauschen) ignorieren zu könnnen, wollen wir dieses auf 10% der LightPollutionRate limitieren. Dazu müssen wir also wissen, wie stark die “LightPollutionRate” ist. Die Himmelshelligkeit an einen bestimmten Beobachtungsort messen wir mit dem Sky Quality Meter (SQM) in Magnituden pro Quadrat-Bogensekunde. Je nach Teleskop und Sensor ergibt sich daraus die “Light Pollution Rate” (in Elektronen pro Pixel pro Sekunde).

Erforderliche Kühlung beim Standard Observer

Light Pollution Rate = 2,35 e- /Pixel / s
Thermal Noise Limit (10%) = 0,235 e- /Pixel /s
Sensor: IMX294
Erforderliche Sensor Tempratur: 17-18 Grad Celsius

Read Noise (Auslese-Rauschen)

Durch den Vorgang des Auslesen der Pixel-Informationen aus dem Sensor ensteht auch ein zusätzliches Rauschen, das sog. Auslese-Rauschen.

Wenn man statt ein paar wenigen Aufnahmen mit längerer Belichtung alternativ viele Aufnahmen mit kürzerer Belichtung macht, hat man auf jeder Einzelaufnahme das Ausleserauschen und das würde also bei “vielen kurzen Belichtungen” viel stärker ins Gewicht fallen. Allerdings ist das Auslese-Rauschen bei modernen CMOS-Kameras sehr gering, wenn man den Gain etwas hoch stellt, was die Dynamik evtl. herabsetzt.

Read Noise bei unterschiedlichem Gain bzw. ISO

Das Aufdrehen des “Gain” bei CMOS-Sensoren ist einfach eine Verstärkung aller Bildsignale.

Das Ausleserauschen (Read Noise) wird durch den Gain allerdings nicht verstärkt, da diese Verstärkung erst nach der Belichtung des Sensors stattfindet (wo genau entsteht das Ausleserauschen?).

Wichtige Kenngrößen des Sensors (Sony IMX294) sind also:

Ausleserauschen (bekommen wir durch Gain 120 auf unter 2.0 e/pix/sec)
Thermisches Rauschen (bei Kühlung auf -10 Grad praktisch Null)
Quantum Efficiency bei 75%

Abbildung 3: Read Noise in Abhängikeit vom Gain bei der ZWO ASI294MC Pro (Google Drive: RobinGlover-02.jpg)

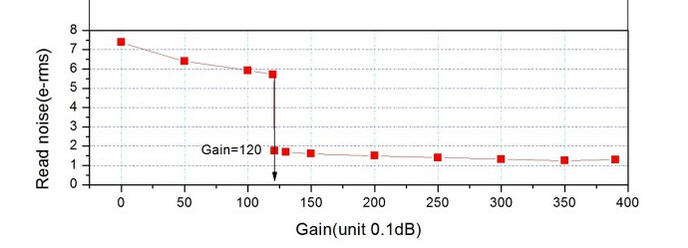
Bekämpfung des Ausleserauschens

Das Auslese-Rauschen können wir bei CMOS-Kameras bekämpfen durch Aufdrehen des Gains bis zu dem Punkt, wo das Ausleserauschen stark abfällt (Gain 120 im obigen Beispiel).
Andererseits ist das Ausleserauschen ja unabhängig von allen anderen Einstellungen und fällt eben genau einmal pro Einzelfoto an. Bei gegebener Gesamtbelichtungszeit sollten wir also mit möglicht wenigen Einzelfotos (Sub Exposures) auskommen. Die Belichtungszeit der Subs also soweit hochdrehen, bis “Hintergrundlimitierung” (s. Lichtverschmutzung unten) erreicht ist.

Schlussfolgerung für das Ausleserauschen

Das Ausleserauschen unseres Sensors pro Einzelbild ist ein unvermeidlicher Einflussfaktor; im Beispiel der ZWO ASI 294MC Pro:
R = 1,5 e-/pixel/sec

Shot Noise (Schrotrauschen)

Auch im eigentlichen Nutz-Signal haben wir ja ein Rauschen, das sog. “Shot Noise” (im Deutschen auch “Schrotrauschen” genannt) – benannt nach Walter Schottky (1886-1976). Das Shot Noise haben wir weil die Photonen diskrete Teilchen sind, deren Ankommensrate auf einem Pixel zufällig ist und die man mit einer Poisson-Verteilung beschreiben kann.

Wenn wir länger belichten, kommen mehr Photonen auf den Sensor, wenn wir kürzer belichten, kommen weniger Photonen auf den Sensor. Bei einem schwächeren Signal ist das Shot Noise im Verhältnis zum Signal größer (Poisson-Verteilung). Umgekehrt: je länger wir belichten, desto geringer wird das Shot Noise im Verrhältnis zum Signal.

Shot Noise als Funktion des Signals

Das ShotNoise hängt von der Stärke des ObjektSignals ab, welches seinerseits durch die Helligkeit des Objekts und die Dauer der Belichtung gegeben ist.

\((9) \hspace{1 em} ShotNoise = \sqrt{ObjektSignal} \)

Wobei die Stärke des ObjektSignals einfach die Anzahl Elektronen pro Pixel ist; was mit der Belichtungszeit ansteigen würde.

Siehe auch: GeoGebra

Abbildung 4: How Shot Noise varies with Brightness (GitHub: Robin Glover Shot Noise 01.svg)

Robin Glover Shot Noise 01.svg

Shot Noise in Prozent des Signals

Absolut gesehen, steigt das Shot Noise mit der Signalstärke, also der Belichtungszeit.
Aber relativ zum Signal wird das Shot Noise (prozentual) immer geringer:

\((10) \hspace{1 em} \Large \frac{Shot Noise}{Signalstärke} = \Large \frac{ \sqrt{Signalstärke} }{Signalstärke} = \Large \frac{1}{\sqrt{Signalstärke}} \)

Wobei auch hier die Signalstärke einfach die Anzahl Elektronen pro Pixel ist; was mit der Belichtungszeit ansteigen würde.

Siehe auch: GeoGebra

Abbildung 5: Shot Noise as a Percentage of Brightness (GitHub: Robin Glover Shot Noise 02.svg)

Robin Glover Shot Noise 02.svg

Shot Noise und Lichtverschmutzung

Das Shot Noise lässt die schwächsten (dunkelsten) Stellen im Bild quasi verschwinden. Das dunkelste im Bild ist aber das Signal der Lichtverschmutzung. Wir sollten das Shot Noise also in Relation zum Signal aus Lichtverschmutzung sehen. Unser “Standard Observer” hat (Gleichung (3)) eine Lichtverschmutzung von 2.35 Elektronen pro Pixel pro Sekunde.

In Abhängigkeit von der Belichtungszeit der Einzelaufnahme ergibt sich:

ShotNoise = Wurzel aus Nutzsignal = Wurzel aus (NutzsignalRate * Belichtungszeit) (nach Gleichung (9) und (3))
LightPollutionSignal = 2.35 * Belichtungszeit (nach Gleichung (5))

und damit

\( ShotNoisePercent = 100 \cdot \frac{ShotNoise}{LightPollutionSignal} = 100 \cdot \frac{\sqrt{Nutzsignal}}{2.35 \cdot Belichtungszeit} = 100 \cdot \frac{\sqrt{NutzsignalRate \cdot Belichtungszeit}}{2.35 \cdot Belichtungszeit} \)

und schließlich:

\( ShotNoisePercent = 100 \cdot \frac{\sqrt{NutzsignalRate}}{2.35 \cdot \sqrt{Belichtungszeit}} \)

Das ShotNoise selber hängt ja von der Stärke des Nutzsignals ab. Bei einer Nutzsignal-Rate von 243,36 Elektronen pro Pixel und Sekunde (243,36 = 15,6²) kommen wir auf das gleiche Bild wie in Robin Glovers Präsentation.

Siehe auch: GeoGebra

Abbildung 6: Shot Noise in % der Lichtverschmutzung des Standard Observers (GitHub: Robin Glover Shot Noise 03.svg)

Robin Glover Shot Noise 02.svd

Dieses Bild sagt ja “Einzelbild länger belichten, ergibt weniger Rauschen”. Aber wenn wir das Stacken (s.u.) mit berücksichtigen, wird die Sache etwas anders.

Sky Noise (Rauschen in Lichtverschmutzung)

Das Rauschen in der Lichtverschmutzung ignorieren wir. Wohl aber ist die Stärke des Signals der Lichtverschmutzung ein wichtiger Massstab für die anderen Faktoren.

Summe des Rauschens im Einzelbild

Wenn wir, wie gesagt die Größe des Dunkelstrom-Rauschens (Thermal Noise) und das Rauschen in der Lichtverschmutzung (Sky Noise) vernachlässigen, da sie klein gegenüber den anderen Rauschkomponenten sind, bleibt also das Gesamt-Rauschsignal im Einzelbild, das “SingleFrameImageNoise” als Summe aus ReadNoise und ShotNoise:

\((11) \hspace{1 em} SingleFrameImageNoise = \sqrt{ReadNoise^2 + ShotNoise^2} \)

Auch dieses Gesamtrauschen im Einzelbild wollen wir in Relation zum Signal aus Lichtverschmutzung (beim Standard Observer) sehen.

\( LightPollutionSignal = LightPollutionRate \cdot Belichtungszeit = 2.6 \cdot t \)

Dabei sehen wir den Einfluss des ReadNoise (Ausleserauschen) auf das Gesamtrauschen, nur bei kürzeren Belichtungszeiten. Bei längeren Belichtungszeiten verschwindet der Einfluss des ReadNoise ganz schnell. Um das in der Grafik sichtbar zu machen, müssen wir einen ganz anderen Massstab auf der x-Achse (Belichtungszeit) wählen.

Das ShotNoise ist \( ShotNoise = \sqrt{SignalRate} \cdot \sqrt{t} \)

Um das gleiche Bild wie in Robin Glovers Vortrag zu kommen, nehmen wir: SignalRate = 2 Elektronen per Pixel per Sekunde

Das ReadNoise hängt von der verwendeten Kamera ab. Wir nehmen für unsere Grafik mal ein paar typische Werte an:

typische CCD-Mono-Kamera habe ein Ausleserauschen (ReadNoise) von 7 Elektronen pro Pixel pro Sekunde
typische CMOS-Kamera habe ein Ausleserauschen (ReadNoise) von 2.5 Elektronen pro Pixel pro Sekunde
eine “ideale” Kamera ohne ReadNoise, also Null Elektronen pro Pixed pro Sekunde

Dann ist bei der typischen CCD-Mono-Kamera (R=7) und einer Belichtungszeit von t das Gesamtrauschen im Einzelbild:

\( SingleFrameImageNoise = \sqrt{7^2 + 2 \cdot t} \)

Und als Prozent des Signals aus Lichtverschmutzung ergibt sich dann für den Standard Observer mit der CCD-Mono-Kamera:

\( ImageNoisePercent = 100 \cdot \frac{\sqrt{7^2 + 2 t}}{2.6 \cdot t} \)

Siehe auch: GeoGebra

Abbildung 7: Single Frame Noise als Prozentsatz vom Signal der Lichtverschmutzung (GitHub: Robin Glover Noise 04.svg)

Robin Glover Noise 04.svg

Stacking

In der Astrofotografie nehmen wir viele kürzer belichtete Fotos eines Objekts auf (sog. Sub Exposures oder Frames) und legen diese dann übereinander sog. Stacking, Dabei addieren sich die Signale in verschiedener Weise.

Signal und Rauschen beim Stacking

Beim Stacken von Einzelaufnahmen (Sub Exposures) verhalten sich Signal und Rauschen unterschiedlich.

Konstante Signale, bei denen sich die Signalstärke von Sub zu Sub eigentlich nicht ändert, addieren sich einfach.

\((12) \hspace{1 em} S = S_1 + S_2 + S_3 + … \)

Rausch-Signale, die sich von Sub zu Sub zufällig (stochastisch) ändern, addieren sich mit der “Quadratwurzel”

\((13) \hspace{1 em} R = \sqrt{ R_1^2 + R_2^2 + R_3^2 + …} \)

Mit zunehmender Anzahl Subs steigt also das Nutzsignal linear und das Rauschen “nur” mit der Quatradwurzel.

Wenn ich also n Subs mit einem Nutzsignal von S₀ und einem Rauschsignal von R₀ zu einem Summenbild stacke, erhalte ich ein Summenbild mit:

Nutzsignal \( S = n \cdot S_0 \)

Rauschsignal \( R = \sqrt{n \cdot R_0^2} \)

und damit eine Signal-Rauschverhältnis im Summenbild von:

\((14) \hspace{1 em}SNR = \frac{S}{R} = \frac{n \cdot S_0}{\sqrt{n \cdot R_0^2}} = \sqrt{n} \frac{S_0}{R_0} \)

Das ist die bekannte Aussage, dass bei einem Summenbild aus vier Subs das Signal-Rauschverhältnis sich verdoppelt etc.

Tabelle 2: Verbesserung des SNR durch Stacking

Spalte 1	Spalte 2	Spalte 3	Spalte 4
Anzahl Frames	Multiplikator Rauschen	Multiplikator Signal	Multiplikator SNR
1	1,00	1	1
2	1,41	2	1,41
4	2,00	4	2,00
10	3,16	10	3,16
20	4,47	20	4,47
50	7,07	50	7,07
100	10	100	10

Wobei die Spalte 2 “Rauschen” noch detaillierter betrachtet werden muss, weil wir es mit mehren Rausch-Quellen zu tun haben, die sich addieren…

\( (15) \hspace{1 em} MultiplikatorRauschen = \sqrt{AnzahlFrames} \\ \\ \)

\( (16) \hspace{1 em}MultiplikatorSignal = AnzahlFrames \\ \\ \)

\( (17) \hspace{1 em} MultiplikatorSNR = \frac{MultiplikatorSignal}{MultiplikatorRauschen} = \frac{AnzahlFrames}{\sqrt{AnzahlFrames}} = \sqrt{AnzahlFrames} \)

Effekt von Stacking auf den Speicherplatz

Andererseits nimmt bei zunehmendem Stacking (Anzahl Frames) der Speicherplatz für die Fotos auch linear zu. Beispielsweise bekomme ich eine Gesamtbelichtungszeit von 120 Minuten wenn ich 720 Fotos mit 10 Sekunden mache oder auch bei 60 Fotos mit 120 Sekunden; allerdings benötigt man in ersteren Fall 12 Mal so viel Speicher.

Die Schlußfolgerung für den Standard Observer

Wenn wir einfach einen gegebenen Ort, ein gegebenes Astro-Equipment und eine gegebene Zeit haben, was sollen wir machen?

Dafür gibt es eine Formel. Wobei wir folgende Symbole benutzen:

O = Object Signal Rate in Electrons per Sekunde per Pixel (abhängig von der Objekt-Helligkeit)
R = Read Noise (typisch bei CMOS-Sensoren: 0,2 e pro Pixel)
T = Total Imaging Time
s = Sub Exposure Time
n = Number of Subs \( n = \frac{T}{s} \)
P = Light Pollution Rate in Electrons per Sekunde per Pixel (typisch: 2,6 für unseren Standard Observer mit Bortle=5)

Noise im Single Frame

Wir wollen die Stärke des Rauschens im Einzelfoto ermitteln. Dafür gilt (Thermal Noise durch geeignete Kühlung vernachlässigt, SkyNoise vernachlässigt weil ganz gering):

\((18) \hspace{1 em} SingleFrameTotalNoise = \sqrt{SingleFrameReadNoise^2 + SingleFrameShotNoise^2} \)

Das SingleFrameShotNoise hängt vom Objekt und von der Belichtungszeit ab:

\((19) \hspace{1 em}SingleFrameShotNoise = \sqrt{s \cdot O} \)

Wenn wir als Objekt einfach mal ein sehr dunkles Objekt nehmen, was eine ObjectSignalRate (O) hat, die genauso groß ist, wie die Rate der Lichtverschmutzung (P), dann ergibt sich:

\((20) \hspace{1 em}SingleFrameShotNoise = \sqrt{s \cdot P} \)

Wenn wir das oben in (18) einsetzen, erhalten wir das Gesamtrauschen im Einzelfoto (genau wie in Robin Glovers Vortrag) als:

\((21) \hspace{1 em} SingleFrameTotalNoise = \sqrt{R^2 + s \cdot P} \)

Noise im Total Stack

Wenn wir jetzt “stacken”, haben wir (wenn wir wieder Thermal Noise und Sky Noise vernachlässigen) ein Gesamtrauschen (TotalStackNoise) von :

\((22) \hspace{1 em} TotalStackNoise = \sqrt{TotalStackReadNoise^2 + TotalStackShotNoise^2} \)

Dabei ist das gesamte ReadNoise im gestackten BIld:

\((23) \hspace{1 em} TotalStackReadNoise = \sqrt{n \cdot R^2} \)

und das gesamte ShotNoise im gestackten Bild:

\((24) \hspace{1 em} TotalStackShotNoise = \sqrt{T \cdot O} \)

Wenn wir als Objekt einfach mal ein sehr dunkles Objekt nehmen, was eine ObjectSignalRate (O) hat, die genauso groß ist, wie die Rate der Lichtverschmutzung (P), dann ergibt sich:

\((25) \hspace{1 em} TotalStackShotNoise = \sqrt{T \cdot P} \)

Wenn wir das beides oben in (22) einsetzen, erhalten wir als Gesamtrauschen im gestackten Bild (genau wie in Robin Glovers Vortrag) als:

\((26) \hspace{1 em}TotalStackNoise = \sqrt{n \cdot R^2 + T \cdot P} \)

Wenn wir diese “trockene” Formel mal als Grafik darstellen, sehen wir besser, was da eigentlich passiert. Wir gehen von einer Gesamtbelichtungszeit von einer Stunde (3600 Sekunden) aus nehmen unseren “Standard Observer” und stellen dann die Werte für zwei Kameratypen (typische CCD mit 7.0 e Ausleserauschen und eine typische CMOS mit 2.5 e Ausleserauschen) dar:

Siehe auch: GeoGebra

Abbildung 8: Total Stack Noise in Abhängigkeit von der Einzel-Belichtungszeit

Robin Glover Noise 05.svg

Beim gesamten Störsignal (Rauschen) betrachten wir ja nur noch zwei Anteile: Ausleserauschen und Lichtverschmutzung.
Die Lichtverschmutzung hat an unserem Beobachtungsort eine gegebene konstante Rate. Die Lichtverschmutzung nimmt auf unseren Bildern also propotional der Belichtungszeit zu – dagegen können wir nichts machen.
Das Ausleserauschen haben wir einmal pro Einzelfoto. Also im Idealfall nur genau einmal. Wenn wir die Gesamtbelichtungszeit in mehrere Einzelfotos (Sub Exposures) aufteilen, haben wir das Ausleserauschen addiert für jedes Einzelfoto. Solange das Ausleserauschen sehr klein gegenüber er Lichtverschmutzung ist, können wir es (fast) vernachlässigen. Wenn wir zu sehr vielen Einzelfotos (d.h. sehr kurzen Belichtungszeiten) kommen wird irgendwann das Ausleserauschen relevant werden und schließlich auch deutlich mehr als die Lichtverschmutzung werden.

Wir sehen, dass sich das Total Stack Noise bei gegebener Gesamtbelichtungszeit (hier: 3600 Sekunden) jeweils einem Optimum (Minimum) annähert (im Beispiel: 96,8 bei CMOS und 97,0 bei CCD).

Die Kurven flachen sehr schnell ab, also können wir durchaus mit Sub Exposures arbeiten, die wesentlich kürzer sind und dabei das optimale (minimale) Rauschen nur ganz knapp erhöhen.

Das Minimum-Rauschen ist also für unseren Standard Observer (P=2.6) bei einer Stunde Gesamtbelichtungszeit:

\( (27) \hspace{1 em} TotalStackNoise_{min} = \sqrt{R^2 + T \cdot P} \)

Für unsere typische CMOS-Kameramit R=2.5 ergibt das:

Minimum-Rauschen CMOS = 96.8 e-/Pixel/s

Für unsere typische CCD-Kamera mit R=7 ergibt das:

Minimum-Rauschen CCD = 97.0 e-/Pixel/s

Wenn wir etwa ein 5% höheres Rauschen als das Minimum-Rauschen akzeptieren, landen wir bei Sub Exposures von: einer halben Minute bei CMOS und 3 Minuten bei CCD.

Im Beispiel sind das:

Standard-Beobachter CMOS 23 sec
Standard-Beobachter CCD 174 sec

Als tabellarische Darstellung haben wir:

Tabelle 3: Ergebnisse: Total Noise in the Stack Bortle=5

Spalte 1	Spalte 2	Spalte 3	Spalte 4	Spalte 5
Sub Exposure Length	Total Stack Noise CMOS	Total Stack Noise CCD	Total Stack Noise CMOS	Total Stack Noise CCD
[s]	e/pixel/s	e/pixel/s	[%]	[%]
1	178,5	431,0	184,4	444,3
2	143,6	312,3	148,3	322,0
5	117,7	211,3	121,6	217,8
10	107,7	164,3	111,3	169,4
23	101,6	130,0	105,0	134,0
30	100,5	123,5	103,9	127,3
60	98,7	110,9	101,9	114,3
100	97,9	105,5	101,2	108,7
174	97,4	101,9	100,7	105,0
1000	96,9	97,7	100,1	100,7
3600	96,8	97,0	100,0	100,0

Mit folgenden Annahmen

T = 3600 Sekunden
P = 2.6 e-/pixel/s
R CMOS = 2,5
R CCD = 7.0

ergibt sich Spalte 2

\( TotalStackNoiseCMOS = \sqrt{\frac{3600 \cdot R^2}{SubExposureLength} + 3600 \cdot P} \)

und Spalte 3:

\( TotalStackNoiseCCD = \sqrt{\frac{3600 \cdot R^2}{SubExposureLength} + 3600 \cdot P} \)

und Spalte 4:

Spalte 4 = Spalte 2 / Maximum von Spalte 2

und Spalte 5:

Spalte 5 = Spalte 3 / Maximum von Spalte 3

Optimale Sub Exposures

Die Idee ist nun, das Rauschen bei einer bestimmten (kürzeren) Belichtungszeit “s” in Relation zum erzielbaren Minimum (also ein lang belichtetes Foto) zu setzten.

Wenn man also einen bestimmten Prozentsatz zusätzlichen Rauschens im Bild akzeptieren will, kann man in der obigen Tabelle 3 für den “Standard Observer” ablesen, welche Einzelbelichtungszeiten dann im Minimum einzuhalten sind (damit das Ausleserauschen nicht zu groß wird). Beispielsweise bei 5% akzeptiertem Zusatzrauschen (also insgesamt 105%, entsprechend 1,05) hat man Einzelbelichtungszeiten von 23 bzw. 174 Sekunden.

Wir können das auch ausrechnen, indem wir unsere Formel nach s (Einzelbelichtungszeit) auflösen:

\( TotalStackNoisePercent(s) =100 \cdot \Large \frac{TotalStackNoise(s)}{TotalStackNoise(3600)} \\\\ \)

Eingesetzt ergibt das:

\( TotalStackNoisePercent(s) =100 \cdot \Large \frac{\sqrt{\frac{3600 \cdot R^2}{s} + 3600 \cdot P}}{\sqrt{R^2 + 3600 \cdot P}} \\\\ \)

Diese Gleichung lösen wir jetz nach s (Einzelbelichtungszeit) auf:

\( (TotalStackNoisePercent)^2 \cdot (R^2 + 3600 \cdot P) = \frac{3600 \cdot R^2}{s} + 3600 \cdot P \)

Wir bringen den Term mit s auf die linke Seite:

\( \frac{3600 \cdot R^2}{s} = (TotalStackNoisePercent)^2 \cdot (R^2 + 3600 \cdot P) – 3600 \cdot P \)

und erhalten schließlich:

\( s = \frac{3600 \cdot R^2}{(TotalStackNoisePercent)^2 \cdot (R^2 + 3600 \cdot P) – 3600 \cdot P} \)

Der Physiker in mir sagt, R (das Ausleserauschen) ist sehr klein. dann ist R² erst recht klein und kann gegenüber 3600 * P ganz vernachlässigt werden. Wir können danach auch die 3600 herauskürzen und erhalten:

\( s = \frac{R^2}{(TotalStackNoisePercent)^2 \cdot P – P} \)

Wenn wir jetzt das TotalStackNoisePercent als “E” schreiben und P unten ausklammern, erhalten wir:

\( (28) \hspace{1 em} \Large s = \frac{1}{E^2 -1} \frac{R^2}{P}\)

Wenn wir 5% zusätzliches Rauschen akzeptieren, also E = 1,05 dann ist der Vorfaktor:

\( \frac{1}{1,05^2 – 1} = 9,7561 \)

Bei E=5% erhalten wir die Formel:

\((29) \hspace{1 em} S = 10 \cdot \frac{R^2}{P} \)

Schlussfolgerungen für meine präferierten Beobachtungsorte

Meine präferierten Beobachtungsorte

An verschiedenen Orten haben wir ganz unterschiedliche Lichtverschmutzung:

Hamburg-Eimsbüttel: SQM 18,0 –> Bortle 8,0
Handeloh Aussensternwarte: SQM 21,1 –> Bortle 3,6
Kiripotib, Namibia: SQM 21,9 –> Bortle 1
Elmshorn: SQM 20,5 –> Bortle 4,4

Meine Kamera

ZWO ASI294MC Pro

CMOS Colour
Pixelgröße: 4,63 μ
Quantum Efficiency: 75%
Ausleserauschen R = 1,5 e-/pixel/s

Quellen: https://astronomy-imaging-camera.com/product/asi294mc-pro-color

Meine Teleskope

Teleskop ED80/600 mit Reducer – Öffnungsverhältnis: f/6.4
Teleskop: APM APO 107/700 mit Reducer 0,75 – Öffnungsverhältnis: f/4,9

Meine Light Pollution Raten

An meinen Beobachtungsorten ist die Lichverschmutzung (in SQM) anders als beim angenommenen “Standard Observer” Bortle 5 (SQM=19,8 mag).
Auch habe ich andere Teleskope und andere Kameras bei mir zur Verfügung.

Tabelle 4: LightPollutioRate an meinen Standorten

Standort	SQM	Teleskop (f Ratio)	Imager (Sensor)	Imager (Pixelsize)	Imager (QE)	LightPollutionRate
Eimsbüttel	18,0	ED80/510 (f/6.375)	Colour	Canon EOS 600D (4.3μ)	41%	3,9
Eimsbüttel	18,0	ED80/510 (f/6.375)	Colour	ASI294MC Pro (4.63μ)	75%	8.27
Handeloh	21,1	ED80/510 (f/6.375)	Colour	Canon EOS 600D (4.3μ)	41%	0,41
Handeloh	21,1	ED80/510 (f/6.375)	Colour	ASI294MC Pro (4.63μ)	75%	0.48
Elmshorn	20,5	ED80/510 (f/6.375)	Colour	ASI294MC Pro (4.63μ)	75%	0,83
Kiripotib	21,9	APM APO 107/700 * 0,75 (f/4,9)	Colour	Canon EOS 600D (4.3μ)	41%	0,18
Kiripotib	21,9	APM APO 107/700 * 0.75 (f/4,9)	Colour	ASI294MC Pro (4.63μ)	75%	0,39

Diese “Light Pollution Rate” liefert also Elektronen pro Sekunde; also immer mehr (linear), je länger wir das Einzelfoto belichten.

Thermisches Rauschen

Das Thermische Rauschen können durch Kühlung des Sensors reduzieren.

Tabelle 5: Light Pollution Rate und erforderliche Kühlung für meine präferierten Beobachtungsorte

Standort	SQM	Teleskop (f Ratio)	Imager (Sensor)	Imager (Pixelsize)	Imager (QE)	Light Pollution Rate	Thermal Noise Limit (10%)	Erforderliche Sensor Temperatur
Eimsbüttel	18,0	ED80/510 (f/6.375)		Canon EOS 600D (4.3μ)	41%	3,9	0,39
Eimsbüttel	18,0	ED80/510 (f/6.375)	Sony IMX294	ASI294MC Pro (4.63μ)	75%	8.27	0.83	ca. +25°
Handeloh	21,1	ED80/510 (f/6.375)		Canon EOS 600D (4.3μ)	41%	0,41	0,04
Handeloh	21,1	ED80/510 (f/6.375)	Sony IMX294	ASI294MC Pro (4.63μ)	75%	0.48	0.05	ca. -15°
Elmshorn	20,5	ED80/510 (f/6.375)	Sony IMX294	ASI294MC Pro (4.63μ)	75%	0,83	0,08	ca. -5°
Kiripotib	21,9	APM APO 107/700 * 0,75 (f/4,9)		Canon EOS 600D (4.3μ)	41%	0,18	0,02
Kiripotib	21,9	APM APO 107/700 * 0.75 (f/4,9)	Sony IMX294	ASI294MC Pro (4.63μ)	75%	0,39	0,04	ca. -15°

In der Spalte “Imager (QE)” haben wir die Quanten-Effizienz des Sensors angegeben (41% gilt für die unmodifizierte Cannon EOS 600D)

Die Spalte “Light Pollution Signal” wurde berechnet mit dem “Sky Background Calculator”: Link: https://tools.sharpcap.co.uk

Wie sich das Thermische Rauschen durch Kühlung reduziert, ist für jeden Sensor anders.

Die Spalte “Erforderliche Sensor Temperatur” ergibt sich aus Abbildung 2 (s.o.) für den Sensor Sony IMX294.

Mein Ausleserauschen

Das Ausleserauschen unseres Sensors pro Einzelbild ist ein unvermeidlicher Einflussfaktor; im Beispiel der ZWO ASI 294MC Pro:
R = 1,5 e-/pixel/sec

Zusammenfassung: Optimale Sub Exposures an meinen Standorten

Bei einer 60 Minuten Gesamtbelichtung habe ich ein den unterschiedlichen Standorten unterschiedliche “optimale” Belichtungszeiten für die Einzelaufname (Sub Exposure),wenn man einen persönlichen Qualitätsanspruch von 5% Zusatz-Rauschen ansetzt.

Tabelle 6: Optimale Einzel-Belichtungszeit

Standort	Lichtverschmutzung SQM [mag/arcsec²]	Teleskop	Kamera	Light Pollution Rate [e-/pixel/s]	Kühlung	Einzel-Belichtungszeit [s]
Eimsbüttel	18,0	f/6,375	ZWO ASI294MC Pro	8,31	+25°	3
Handeloh	21,1	f/6,375	ZWO ASI294MC Pro	0,48	-15°	45
Namibia	21,9	f/4,9	ZWO ASI294MC Pro	0,39	-15°	55

Einzelberechnungen: Optimale Sub Exposures an meinen Standorten

Im Einzelen gehen die hier aufgeführten “optiomalen” Einzel-Belichtungszeiten aus den Tabellen x-y hervor.

Optimale Belichtungszeit in Eimsbüttel (SQM 18,0, P=8,27)

Tabelle 7: Ergebnisse: Total Noise in the Stack in Eimsbüttel

Sub Exposure Length	Total Stack Noise ASI294 MC Pro	Total Stack Noise ASI294MC Pro
[s]	e-/pixel/s	[%]
1	194,6	112,8
2	183,9	106,6
2,64	181,2	105,0
5	177,2	102,7
10	174,9	101,3
20	173,7	100,7
30	173,3	100,4
100	172,9	100,1
300	172,6	100,0
1000	172,6	100,0
3600	172,55	100,0

Mit folgenden Annahmen:

T = 3600 Sekunden
P = 8.27 e-/pixel/s
R = 1,5 e-/pixel/s (ASI294MC Pro, Gain=121)

Optimale Belichtungszeit in Handeloh (SQM 21,1 P=0,48)

Tabelle 8: Ergebnisse: Total Noise in the Stack in Handeloh

Sub Exposure Length	Total Stack Noise ASI294MC Pro	Total Stack Noise ASI294MC Pro
[s]	e-/pixel/s	[%]
1	99,1	238,3
2	76,0	182,7
5	57,9	139,1
10	50,4	121,1
30	44,7	107,5
45	43,7	105,0
60	43,2	103,8
120	42,4	101,9
300	41,9	100,7
1200	41,7	100,1
3600	41,60	100,0

Mit folgenden Annahmen:

T = 3600 Sekunden
P = 0.48 e-/pixel/s
R = 1,5 e-/pixel/s (ASI294MC Pro, Gain=121)

Optimale Belichtungszeit in Kiripotib (SQM 21,9 P=0,39)

Tabelle 9: Ergebnisse: Total Noise in the Stack in Kiripotib

Sub Exposure Length	Total Stack Noise ASI294MC Pro	Total Stack Noise ASI294MC Pro
[s]	e-/pixel/s	[%]
1	97,5	260.0
2	73,9	196,9
5	55,0	146,6
10	47,1	125,5
30	40,9	109,1
55	39,4	105,0
60	39,2	104,6
120	38,4	102,3
300	37,8	100,9
1200	37,6	100,2
3600	37,50	100,0

Mit folgenden Annahmen:

T = 3600 Sekunden
P = 0.39 e-/pixel/s
R = 1,5 e-/pixel/s (ASI294MC Pro, Gain=121)

Wie erziele ich gute Astro-Fotos?

Wie lange sollten die einzelnen Sub-Exposures belichtet werden?

Quellen

Was ist beeinflussbar?

Wir gehen die Thematik in folgenden Schritten an

Grundlagen: Signal und Rauschen

Der digitale Sensor – schematisch

Signalstärke

Messen von Signal und Rauschen

Rauschen

Zusammenfassung (Executive Summary)

Was bedeutet “hintergrundlimitiert” ?

Signalkomponenten im Einzelfoto

Wie addieren sich die Signalkomponenten im Einzelfoto?

Signal vom Himmelsobjekt

Signal vom Himmelshintergrund

Signal vom Dunkelstrom

Rauschkomponenten im Einzelfoto

Wie addieren sich Rauschkomponenten im Einzelfoto?

Thermal Noise (Dunkelstrom-Rauschen)

Erforderliche Kühlung

Erforderliche Kühlung beim Standard Observer

Read Noise (Auslese-Rauschen)

Read Noise bei unterschiedlichem Gain bzw. ISO

Bekämpfung des Ausleserauschens

Schlussfolgerung für das Ausleserauschen

Shot Noise (Schrotrauschen)

Shot Noise als Funktion des Signals

Shot Noise in Prozent des Signals

Shot Noise und Lichtverschmutzung

Sky Noise (Rauschen in Lichtverschmutzung)

Summe des Rauschens im Einzelbild

Stacking

Signal und Rauschen beim Stacking

Effekt von Stacking auf den Speicherplatz

Die Schlußfolgerung für den Standard Observer

Noise im Single Frame

Noise im Total Stack

Optimale Sub Exposures

Schlussfolgerungen für meine präferierten Beobachtungsorte

Meine präferierten Beobachtungsorte

Meine Kamera

Meine Teleskope

Meine Light Pollution Raten

Thermisches Rauschen

Mein Ausleserauschen

Zusammenfassung: Optimale Sub Exposures an meinen Standorten

Einzelberechnungen: Optimale Sub Exposures an meinen Standorten

Optimale Belichtungszeit in Eimsbüttel (SQM 18,0, P=8,27)

Optimale Belichtungszeit in Handeloh (SQM 21,1 P=0,48)

Optimale Belichtungszeit in Kiripotib (SQM 21,9 P=0,39)

Anhang: Lichtverschmutzung

Lichtverschmutzung im Internet