Gehört zu: Physik
Siehe auch: Relativitätstheorie, Vektorraum, Gravitation, Schwarze Löcher, Metrik, Koordinatensysteme

Krümmung der Raumzeit

Die Allgemeine Relativitätstheorie (ART) basiert auf dem Postulat der Äquivalenz von Gravitation und Beschleunigung.

Aus diesem Äquivalenzprinzip ergibt sich die Lichtablenkung in Gravitationsfeldern.

Wenn man trotzdem davon ausgehen möchte, dass das Licht immer den kürzesten Weg nimmt, muss die Gravitation den Raum (besser die Raumzeit) entsprechend krümmen, sodass eine Metrik entsteht bei der der kürzeste Weg zwischen zwei Punkten nicht unbedingt die Euklidische gerade Linie ist.

Wir wollen hier zunächsteinmal den Begriff der “Krümmung” ganz allgemein diskutieren.

Umgangssprachlich denkt man bei “Krümmung”, dass sich etwas in eine zusätzliche Dimension krümmt (s.u. die vielen Beispiele). Bei der von Einstein postulierten Krümmung der vierdimensionalen Raumzeit wird aber für diese Krümmung keine 5. Dimension gebraucht. Die vierdimensionale Raumzeit ist nach Einstein  “in sich” gekrümmt; d.h. wir haben einen anderen Abstandsbegriff (eine andere Metrik, ein anderes Linienelement).

Krümmung bei Euklidischer Metrik

Unter der Krümmung eines geometrischen Objekts versteht man die Abweichung von einem geraden Verlauf; dazu bedarf es (mindestens) einer weiteren Dimension in die die Krümmung verläuft oder der Begriff “gerade” muss umdefiniert werden. Eine Kurve verläuft “gerade” wenn beim Durchlaufen mit konstanter Geschwindigkeit, keine Beschleunigungen “seitwärts”, sonder höchstens in der Normalen auftreten.

Wir betrachten eine Gerade. Solange sie wirklich geradeaus verläuft ist sie nicht gekrümmt. Wenn sie eine Kurve nach links (oder rechts) macht, haben wir eine Krümmung – und wir brauchen dafür (mindestens) eine zweite Dimension. Die Stärke der Krümmung kann mehr oder weniger sanft oder kräftiger sein. Wir messen die Stärke der Krümmung an einer Stelle durch einen sog. Krümmungskreis. Das ist ein Kreis, der sich in dem betrachteten Punkt am besten an die Kurve anschmiegt. Ein großer Krümmungskreis bedeutet eine kleine Krümmung ein kleiner Krümmungskreis ein starke Krümmung. Der Kehrwert des Radius ist das Maß für die Krümmungsstärke.

Die andere Frage ist, welche geometrischen Objekte sind es, die da “gekrümmt” werden?  Im einfachsten Fall ist es eine eindimensionale Linie in einer zweidimensionalen Ebene; also z.B. ein Funktionsgraph oder eine sog. Kurve. Kurven sind in diesem Zusammenhang sehr interessant als Teilmenge eines Vektorraums, die durch eine Abbildung von einem reellen Intervall in den Vektorraum  als sog. “parametrisierte” Kurve dargestellt werden kann. Das “Umparametrisieren” ist dann eine Äquivalenzrelation zwischen parametrisierten Kurven. Eine “Kurve” kann dann als Äquivalenzklasse solcher parametrisierten Kurven verstanden werden. Als Repräsentant einer Äquivalenzklasse nimmt man dann gerne eine nach Bogenlänge parametrisierte Kurve.

Wenn wir uns mit Kurven beschäftigen und speziell dann mit der Länge einer Kurve oder der Krümmung von Kurven, haben wir es mit Differentialgeometrie zu tun.
Dazu gibt es eine Reihe von sehr schönen Youtube-Videos:

• Was ist eine Kurve: https://youtu.be/SKUjWR9stmA
• Umparametrisieren:
• Länge einer Kurve https://youtu.be/H4oLS7CO7H8
• Krümmung einer ebenen Kurve: https://youtu.be/5oOiXZapNKg
• Krümmungskreis: https://youtu.be/4vO8HCK5Hdk

Schritt 1: Krümmung einer Linie in der Ebene

Wenn das betrachtete Objekt ein Funktionsgraph von beispielsweise y = f(x) in der Ebene ist, können wir die Krümmung leicht berechnen:

Für eine zweimal differenzierbare Funktion  y = f(x) ergibt sich der Krümmungsradius an einem Punkt x zu:

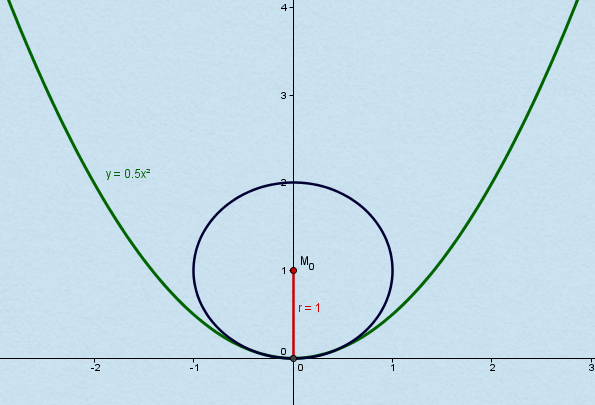
\( \Large  r(x) = \left\vert \frac{(1+(f^\prime(x))^2)^\frac{3}{2}}{f^{\prime\prime}(x)} \right\vert  \)

Als Beispiel nehmen wir mal eine Parabel f(x) = 0,5 * x²
Dazu haben wir die Ableitungen:
f^‘(x) = x
f^“(x) = 1
Der Krümmungsradius beispielsweise am Punkt x₀ = 0 beträgt dann laut obiger Formel:

\( \Large r(x_0) = \frac{(1+{x_0}^2)^{\frac{3}{2}}}{1} = 1 \\\ \)

Und zur Probe nehmen wir noch x=1:

\( \Large r(1) = \frac{(1+1^2)^{\frac{3}{2}}}{1} = 2^\frac{3}{2} = 2 \sqrt{2} \)

Dieses Beispiel habe ich entnommen aus https://www.ingenieurkurse.de/hoehere-mathematik-analysis-gewoehnliche-differentialgleichungen/kurveneigenschaften-im-ebenen-raum/kruemmung/kruemmungsradius.html
Es wird grafisch veranschaulicht durch:

Schritt 2: Krümmung einer Kurve in der Ebene

Wenn das betrachtete Objekt eine “richtige” Kurve in der Ebene ist, wird die Krümmung anders berechnet.

Als “richtige” Kurve (in der Ebene) betrachten wir von der obigen Parabel das Kurvenstück von x=-1 bis x=1. Als Parametrisierte Kurve, wobei der Parameter t auch von -1 bis 1 laufen möge, (was wir uns z.B. als Zeit vorstellen könnten) sieht das dann so aus:

\( \Large \alpha(t) = \left( \begin{array}{c} t \\\ \frac{1}{2}t^2  \end{array}\right)  \\\  \)

Um die Krümmung zu brechnen ermitteln wir zuerst:

\( \Large \alpha^\prime(t) = \left( \begin{array}{c} 1 \\\ t  \end{array}\right)  \)

womit dann:

\( \Large ||\alpha^\prime(t)||^2 =  1 +  t^2   \\\  \)

und mit:

\( \Large \alpha^{\prime\prime}(t) = \left( \begin{array}{c}  0 \\\ 1  \end{array}\right)  \)

ergibt sich:

\( \Large det(\alpha^\prime(t), \alpha^{\prime\prime}(t)) = 1  \\\ \)

und damit ergibt sich dann die Krümmung zu:

\( \Large \kappa_\alpha(t) = \frac{1}{(1 + t^2 )^\frac{3}{2}}  \)

Bei t=0 ist dann die Krümmung:

\( \Large \kappa_\alpha(0) = 1 \\\  \)

und zur Probe nehmen wir noch t=1:

\( \Large \kappa_\alpha(1) = \frac{1}{2 \sqrt{2}} \\\ \)

Weil t=x ist, stimmt das mit den Berechnungen des Krümmungsradius (s.o. Schritt 1) exakt überein.

Schritt 3: Krümmung einer Fläche im Raum

Analog können wir uns gekrümmte Flächen im Raum vorstellen. Hier kann allerdings der Krümmungsradius in unterschiedlichen Richtungen unterschiedlich sein. Inetwa so die wir das von einem Gradienten kennen.

Auch in diesem Fall stellen wir uns das ganz klassisch geometrisch vor als Krümmung in eine weitere Dimension.

Krümmung per Nicht-Euklidischer Metrik

In der Allgemenen Relativitätstheorie spricht man auch von “Krümmung” z.B. Krümmung des Raumes oder Krümmung der Raumzeit.

Hier basiert die “Krümmung” nicht auf einer zusätzlichen Dimension, sondern auf einer speziellen Metrik in ein und demselben Raum. Unter “Metrik” versteht man ja eine Vorschrift, die zwei Punkten in dem betreffenden Raum einen Abstand zuordnet.  So eine Metrik definiert dann auch automatische die Längen von Linien…

Geodätische Linie

Die Linie, die die kürzeste Verbindung zwischen zwei Punkten bildet, nennt man Geodät oder auch Geodätische LInie. Auf der Erdoberfläche kennen wir das z.B. bei der Seefahrt oder Luftfahrt wenn wir beispielsweise die Flugroute von London nach Los Angeles betrachten:

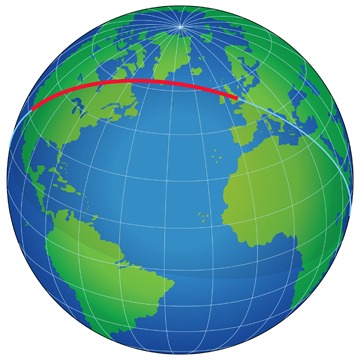
Das Licht läuft immer auf einer Geodäte, nimmt also die kürzeste Verbindung. Das kann “gekrümmt” aussehen…

Krümmung ohne zusätzliche Dimension

Für eine solche Krümmung benötigen wir aber nicht zwingend eine zusätzliche Dimension. Die Krümmung kann auch “in sich” durch andere Abstandsgesetze (= Metriken) bewirkt werden.
Siehe Schwarzschild-Metrik